Title: On the Origin of the Salpeter Slope of the Initial Mass Function
Authors: M. S. Oey
First Author’s Institution: Department of Astronomy, University of Michigan
One of the most basic links between the observable results of star formation and our theoretical understanding of the star formation process is the stellar initial mass function (IMF). This function tells an astronomer the number of stars she should expect per mass bin. Since the 50’s, we’ve known that the upper mass end (above 1 solar mass) of the IMF is well described by a power law,
n(m)dlog(m) ∝ m-Γdlog m
with Γ ~ 1.35. This is known as the Salpeter slope of the IMF, after its discoverer. While the value of the slope is well-measured, a theoretical understanding of its physical origin is lacking. The slope is recovered in simulations of star formation, regardless of the physical processes at work or details of the simulation, and seems to be a generic feature of hierarchical collapse.
The slope its self is puzzling. Stars form in clusters, which are observed to have a mass function of the form,
n(M)dlog(M) ∝ M-Bdlog M
with Β ~ 1.0. Since star clusters and individual stars should form from the same hierarchical fragmentation process, it is strange that the resulting mass functions are similar, but not identical. A slope of 1.0 corresponds to a uniform distribution of mass between small and large scales. The simple Γ = 1.0 also follows from simple theory, because if stars acquire mass by Bondi-Hoyle accretion, then the accretion rate, ṁ, should scale as m2. Using this scaling, and assuming that the number of stars is invariant during mass accretion, one can trivially solve the continuity equation,
(dn/dt) + (d/dm)(ṁn) = 0,
and obtain that n should scale as m-2, which implies dn/dlogM goes as m-1, as expected.
In this paper, the author proposes that the departure from the simple m-1 scaling with mass arises because of a simple fact: the natal molecular cloud must first fragment into clumps, which must in turn fragment into stars. Individual clumps cannot be arbitrarily large, and in fact may have masses comparable to stellar masses. This means that not every clump can fragment into an arbitrarily massive star, implying that once the cluster finishes forming the resulting power-law slope of the mass function should be steeper than m-1, even if individual clumps fragment into a collection of stars with a mass function that goes as m-1.
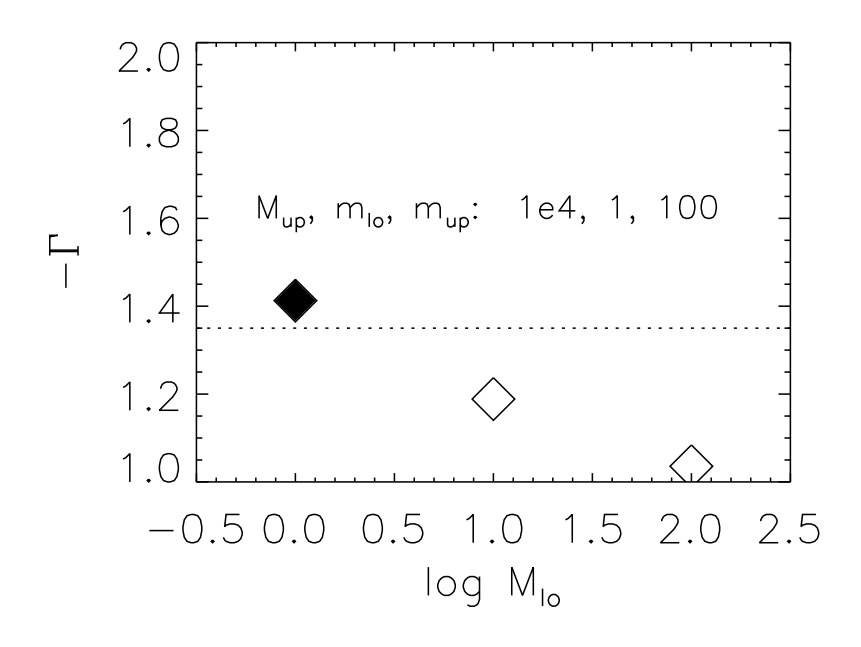
The dependence of the power-law slope of the IMF on the minimum possible mass for a star-forming clump.
To quantify this effect, the author has performed a very simple numerical experiment. She supposes that the mass function of stars and clumps should both scale as m-1, as expected from the simple argument given above. She then forms a cluster by first drawing a clump mass from a clump mass function, then using the clump mass to make a subcluster of stars by drawing from a stellar mass function. If a star is drawn that exceeds the mass of the clump, that star is rejected and new stars are drawn successively until the clump mass is exhausted. The final mass function depends on the low mass and high mass cutoff for stars and clumps.
The conclusion is presented in the figure to the right. The author plots the power-law slope of the IMF as a function of either the minimum possible clump mass Mlo. The maximum possible clump mass, minimum possible stellar mass, and maximum possible stellar mass were set to be 10,000, 1, and 100 solar masses, respectively. She finds that If the smallest possible clump mass is much bigger than a typical star, then the effect of finite clump mass is washed out, causing the resulting stellar mass function to have a power law slope of -1. However, if the lowest possible clump mass is comparable to a typical stellar mass, then sampling effects become important, steepening the mass function to a value comparable to the Salpeter slope. Since clumps are observed down to masses comparable to one solar mass, this is a viable explanation for the steep slope of the Salpeter IMF.

Trackbacks/Pingbacks