- Title: An Infrared Divergence in the Cosmological Measure Theory and the Anthropic Reasoning
- Author: A. V. Yurov, V. A. Yurov, A. V. Astashyonok
- First and Second Author’s Institution: Russian State University of I. Kant
Modern cosmology, at its most basic level, can be summed up by the Friedmann Equations. These equations, derived from Einstein’s general relativity by Alexander Friedmann in 1922, describe how an isotropic, homogeneous Universe expands from an initial singularity, depending on the relative abundances of the Universe’s constituents (e.g. baryonic matter, radiation, etc.). For example, if the Universe was made only of photons, the Friedmann Equations predict that the Universe would expand at a rate of , where
is the age of the Universe.
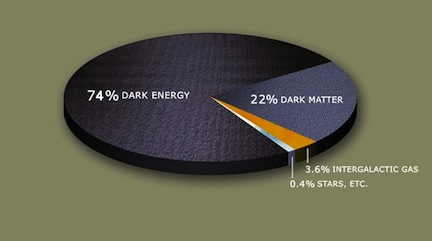
The Cosmic Pie: This figure shows modern estimates of the mass-energy ingredients in our Universe. Copied from Wikipedia.
The fact–determined relatively recently–that our Universe is not only expanding, but that its expansion is accelerating, has led most cosmologists to accept the existence of an additional cosmological ingredient: dark energy. According to mainstream cosmology, this seems to be a strange form of energy which does not dilute (If you take a box containing some dark energy, then double the size of the box, you now have double the amount of dark energy you did before). Furthermore, it takes up a significant fraction of the total mass-energy of the Universe– roughly 74% (see pie chart). Dark energy can be parametrized in the Friedmann equation through a term called the “cosmological constant” . Similar to the radiation case considered above, in a Universe dominated by dark energy, the size of the Universe grows exponentially as
.
- The Universe today seems to be dark-energy-dominated, which is why it is beginning to expand at an accelerating rate. Since the growth of a dark-energy-dominated Universe like ours depends on the factor
The Anthropic Principle
The anthropic principle is one way of answering the question posed above. It essentially argues that we see such a strange value of in our Universe because most other values of
are not conducive for life to exist at all. For example, Steven Weinberg argued that if
was much higher than the value we observe, the Universe would expand too fast for large-scale structure (and hence, life!) to form. Any sentient observer looking out and measuring the cosmological constant should only measure values that are consistent with the sentient observer existing in the first place!
If this approach seems a bit strange to you, you are in good company; the anthropic principle is one of the most hotly debated ideas in modern cosmology. Ignoring the philosophy-of-science discussion that rages over calling such a principle “scientific”, the anthropic principle clearly depends on a multiverse hypothesis, or the idea that there must be infinitely many Universes, where different Universes can have different values of (or the fine structure constant, etc.).
Calculating Probabilities
In order to mathematically formalize the anthropic principle, we need some way to determine the “probability” of an observer somewhere in the Multiverse looking out and observing a given value of . But when we consider the fact that there are infinitely many Universes, the idea of assigning probabilities becomes perilous.
A little more background: without getting into the technical details of string theory, we note that our current understanding of string theory implies that there are about different Universes that have
. On the other hand, it appears that the number of Universes with $Lambda ≤ 0$ is actually infinite. Furthermore, there’s no obvious reasons why life can’t exist in Universes with small, negative values of
.
Let us imagine we understood string theory, but that we did not know what the value of the cosmological constant was in our Universe. Furthermore, our goal is to test the multiverse hypothesis. If the multiverse hypothesis is correct, then there are infinitely many more Universes with negative than with positive
, and that both could support life, then, by the anthropic principle, we would have to conclude that we are much more likely to live in a Universe with
≤ 0. In fact, due to the fact that there are only finitely many Universes with
, the probability that we live in such a Universe is exactly 0. But we, as human beings, do live in a Universe where
. This seems to show conclusively that the multiverse hypothesis is false.
The paper shows a way to recover the multiverse hypothesis and anthropic reasoning based on two distinct results, but we will focus on the first in this astrobite. The authors argue that the fact that an event has zero probability does not mean that it is impossible. To quote the paper:
“Suppose a certain event A has a zero probability: p(A) = 0. Does it mean that A cannot happen? The answer is: not necessarily. Those events that cannot happen are called impossible. The probability of an impossible event is zero ad definition, but the opposite is simply not true. The probability to hit a direct center of a target is zero, but is not impossible. The probability to guess number 42 out of all possible real numbers is also zero, but it can happen nevertheless. And, finally, the probability to find ourselves at one particular point in infinitely large universe is also zero, yet we are here!”
In other words, we must be careful to distinguish between “explaining” and “predicting”, based on what information the observer has. Different amounts of information lead to different probability estimates (this is a basic result of Bayesian probability theory). After applying the prediction-based probabilites (as discussed above) and found the probability of to be 0, when you measured
, you would not be able to conclude that the multiverse does not exist. Rather you would need to use “explanation-based” probabilities, which are shifted from the old probabilities based on the fact that you now know the value of
! The authors show, using this method, that once you know you exist in a Universe with
, then the probability of a multiverse existing is still nonzero. Hence, the anthropic principle and the multiverse it depends on are not, in this case at least, at odds with the empirical fact that in our Universe

But the sample size of the universe is just one, so how does working out the probabilities of the universe having particular properties make any sense? The anthropic principle is just a way for us to hide our ignorance.
Good question Cathy. The authors consider this very reasonable concern and this is a brief sketch of their argument:
Let us consider a toy multiverse with just two types of Universes, type 1 and type 2. Suppose that we were to conduct an experiment with two possible outcomes A and B, so that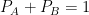 . Then the probabilites for the outcomes are proportional the amount of A and B outcomes in the entire multiverse:
. Then the probabilites for the outcomes are proportional the amount of A and B outcomes in the entire multiverse:  . Now
. Now 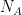 is just
is just  where
where 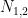 is the number of type 1 (2) Universes and
is the number of type 1 (2) Universes and  is the number of A events in type 1 (2) Universes.
is the number of A events in type 1 (2) Universes.  is calculated in a similar way. If we now solve the two equations for
is calculated in a similar way. If we now solve the two equations for  and
and  , then—in the straightforward case where none of the N’s above are infinite— then we now have a well-defined measure of the probability that an observer has to measure A or B, even if she does her measurements in just a single Universe.
, then—in the straightforward case where none of the N’s above are infinite— then we now have a well-defined measure of the probability that an observer has to measure A or B, even if she does her measurements in just a single Universe.
Perhaps your concern is related to the fact that to even know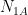 or
or 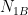 we should make scientific measurements of these numbers, but this is impossible since to measure them both we would need to be able to make measurements in both Universes. This is certainly a valid concern. The authors concede that in these arguments, they need to introduce an a priori probability distribution
we should make scientific measurements of these numbers, but this is impossible since to measure them both we would need to be able to make measurements in both Universes. This is certainly a valid concern. The authors concede that in these arguments, they need to introduce an a priori probability distribution  over the multiverse, one that exists despite our inability to directly pin it down through measurement in each Universe. This part might seem pseudo-scientific to you. On the other hand, it might be possible for physicists to eventually derive
over the multiverse, one that exists despite our inability to directly pin it down through measurement in each Universe. This part might seem pseudo-scientific to you. On the other hand, it might be possible for physicists to eventually derive  from first principles, in which case the earlier result still holds: the result that measurements in a single Universe still have well-defined probabilities which are defined over the multiverse.
from first principles, in which case the earlier result still holds: the result that measurements in a single Universe still have well-defined probabilities which are defined over the multiverse.
A wonderful post describing something bordering on a philosophical approach to our perception of the universe(s) .