- Title:Effects of Biases in Virial Mass Estimation on Cosmic Synchronization of Quasar Accretion
- Author: Charles L. Steinhardt
- First Author Institution: IPMU, University of Tokyo
Introduction
As has been discussed in a number of astrobites posts, the study of quasars (a specific type of active galactic nucleus, or AGN) is important because their evolution appears to be closely linked to the evolution of many other parts of the cosmos, from structure formation and reionization of the universe to the growth and structure of their host galaxies. In recent years, large catalogs of quasars from projects like the Sloan Digital Sky Survey as well as accurate mass estimates for these objects have led to important and sometimes puzzling findings. In this paper, the author discusses some of the results from studies of Type 1 quasar accretion that do not agree with current models. In particular, he discusses how the results of these studies change if the method of measuring the quasar masses is biased.
Type 1 Quasars and Virial Mass Estimates
As I mentioned in a previous post, quasars are most commonly classified according to their spectra, with the two largest categories consisting of broad-line or “Type 1” quasars, and narrow-line or “Type 2” quasars. An example of the differences in the two spectra can be seen in the figure below.
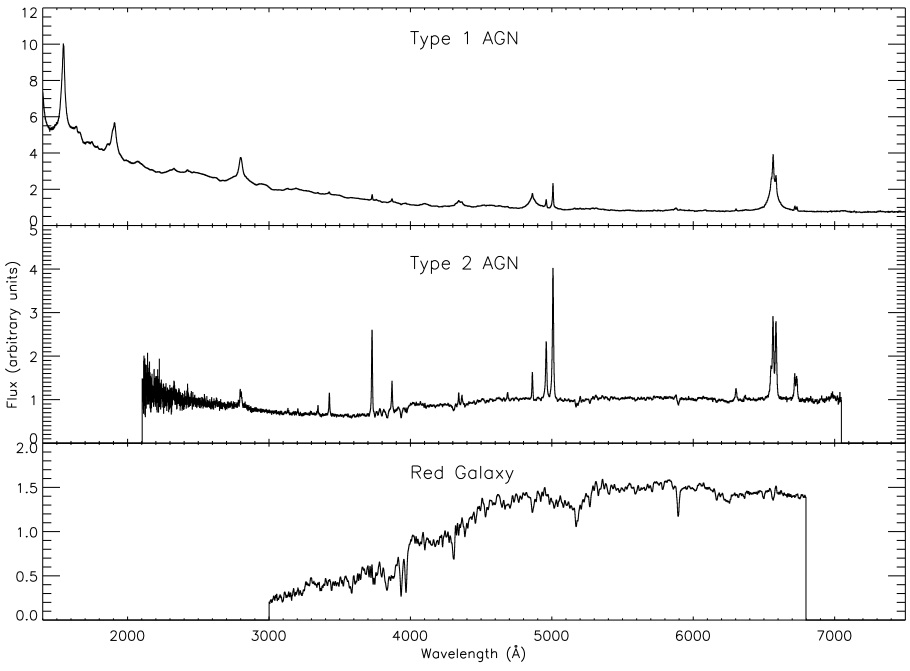
This figure (from Trump et al. 2008) shows examples of three types of spectra: a broad-line AGN, a narrow-line AGN, and a normal elliptical galaxy.
Because the broad lines in a Type 1 quasar spectrum are thought to come from rapidly moving gas in the quasar accretion disk, astronomers can use the width of the emission lines to estimate the mass of the black hole, by assuming that gas is at a certain radius and then calculating what gravitational potential could “hold on” to gas that is moving at the speed indicated by the Doppler broadening of the lines. Because these estimates rely on the Virial Theorem (which relates the kinetic energy of the gas to the gravitational potential in which it is moving), they are known as virial mass estimates. They are sometimes also called “scaling relations,” since they scale the mass of the black hole to the width of the broad emission lines.
The Mass-Luminosity Relationship
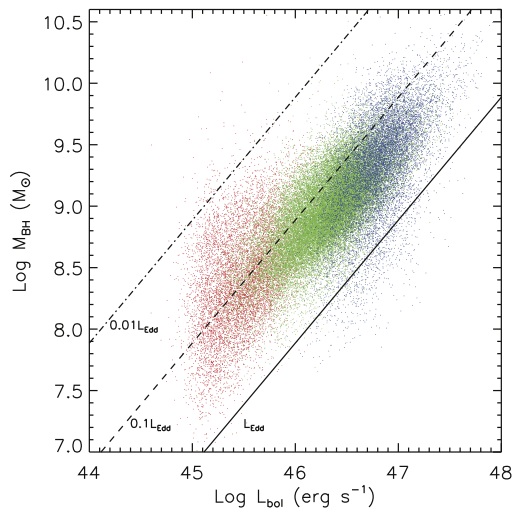
This figure (from Shen et al. 2008) shows the mass-luminosity relationship for a large sample of SDSS quasars.
One of the most fundamental relationships that one can examine in AGN science is that between quasar mass and luminosity. Just because it is fundamental does not, however, mean that it is easy to explain. Shown at right is an example of a mass-luminosity diagram created using virial mass estimates of Type 1 quasars in the SDSS quasar catalog. The different colors of quasars in the diagram represent which emission line was used to calculate their mass: red for , green for Mg II, and blue for C IV. (See this astrobite for a quick explanation of spectral line naming conventions.) The line used is based on the quasar’s distance – quasars at different redshifts will have different parts of their spectra visible in the optical bands of the SDSS, and therefore emission lines at different wavelengths become accesible. In this paper, the author examines solely those quasars in the redshift range from 0.2 < z < 2, because this is the range in which the Mg II line can be seen. Another important feature to note in the figure at right is the solid line indicating the Eddington Luminosity, a quantity which depends only on the quasar mass. As can be seen in the figure, the bolometric luminosity,
, of nearly all Type 1 quasars is between the Eddington Luminosity and 1% of the Eddington luminosity. Because
is directly related to the accretion rate of the black hole, one of the large mysteries in quasar science is the tight correlation between mass and luminosity, since there is no particular reason that Type I quasars at a given mass should have such a narrow range of accretion rates.
What are the effects of systematic biases?
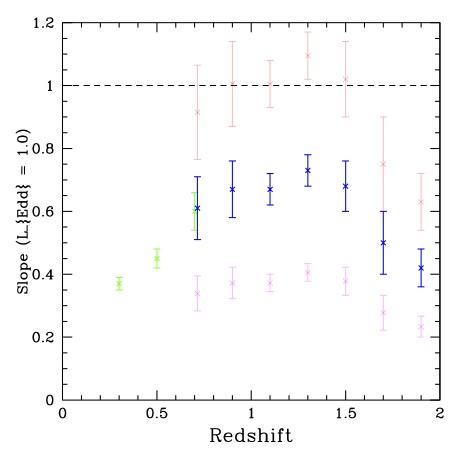
This plot shows the slope of the sub-Eddington luminosity boundary of the quasars in the sample as a function of redshift. The different colors represent four different virial mass calibrators: H_beta (green) and Mg II (blue) are essentially the "control sample" in the study, while red uses the compressive Mg II mass correction, and magenta uses the expansive Mg II mass correction.
The author of this paper investigates the resulting changes in the quasar mass-luminosity diagram if the Mg II virial mass estimates are biased in either of two ways. He first looks at a compressive correction to the mass estimates, suggested by Rafiee & Hall (2010), which would result in a narrower mass distribution of quasars at a given redshift. He then investigates an expansive correction, suggested by Risaliti, Young, & Elvis (2009), which would result in a wider distribution of quasar masses at a given redshift. Shown in the figure at left, the main difference between the three mass estimates shows up in the way the luminosity of the quasars at a given redshift depends on their mass. Using the original mass estimates, Shen et al. (2008) calculate . This dependence is currently unmatched by any physical model. Using the compressive correction, the author derives
. This linear relationship between mass and luminosity indicates that the characteristic accretion rate might be solely due to gravitational effects of the black hole. Using the expansive correction, the author derives
. This relationship could be described by a physical model which balances gravitational and non-gravitational effects, for example one by Thompson et al. (2005) in which quasar accretion and star formation compete for infalling gas, yielding
.
In addition to the luminosity dependence, the author discusses a number of other puzzling behaviors that are derived from the quasar mass-luminosity plane, which do not change regardless of any correction made to the mass estimates. These include the fact that quasars of same mass at the same redshift all have similar luminosities, and the fact that quasar luminosities are time dependent – as one moves to lower redshift, the quasar luminosities decrease across the board. The fact that these two puzzles (and a couple of others) cannot be solved even by taking account of possible biases in the mass estimates indicates, according to the author, that “we must conclude that we do not understand how SMBH [super massive black holes] are born, we do not understand how they grow, and we do not understand how they die.” Needless to say, it seems that the study of quasars will remain an interesting subject for astrophysicists for quite some time.


You mention type 1 and 2 quasars. I thought that these types were reserved for descriptions of Seyfert and that just about all Quasars were broad emission spectrum objects.