Title: BEER analysis of Kepler and CoRoT light curves: Discovery of a hot Jupiter with superrotation evidence in Kepler data
Authors: Faigler, S., Tal-Or, L., Mazeh, T., Latham, D. W., and Buchhave, L. A.
First Author’s Institution: School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel
The Background
The Kepler telescope is great at finding transiting planets by looking for small, periodic dips in stellar light curves. Unfortunately, it is also great at finding things that look like transiting planets but are actually something else. Brown dwarfs, the size of Jovian planets but tens of times as massive, can mimic a planetary transit, as can eclipsing binary stars situated behind a lone Kepler target. As we’ve discussed, the false positive rate is believed to be low: about 90 percent of planet candidates are likely true planets. While reassuring to those studying planet populations, this lingering ten percent chance is troubling to anyone interested in an individual system. To confirm individual transiting systems in the pre-Kepler era, radial velocity observations have often been collected to measure the Doppler “wobble” of the host star. However, since many of Kepler‘s planets are quite small and its stars very faint, radial velocity observations can be very difficult and time-consuming to obtain.
The Method
Recently, some groups have attempted to confirm planetary systems without additional data beyond that collected and publicly available from the Kepler mission. The most successful method so far has been the analysis of transit timing variations, when mutual gravitational interactions between planets in one system change the velocities of planets, causing their transits to occur systematically earlier or later than expected. While successful, this method requires at least two planets in orbit: a “lonely” planet would not have anything to perturb it during its orbit to induce timing variations. So-called “Hot Jupiters,” bodies with the mass of Jupiter but in few-day periods, tend to be in such lone systems, meaning transit timing can not be used to confirm these systems.
Faigler et al. apply a technique to confirm giant planet systems: instead of analyzing the individual transits of these planets, the authors study the rest of the light curve, looking at what happens when the planet is not transiting. They note three effects which can be observed as the planet orbits its host star. The first is reflected light. During an orbit, we can observe reflected starlight bouncing off the surface of the planet. Much like we observe for the Moon and inner planets, the amount of reflected light we can observe changes during the orbit as the companion moves from “new planet” at the transit to “full planet” half a period later. Since the amount of reflected light depends on the surface area of the planet, its magnitude is related to the radius of the planet.
Artist’s impression of a “contact binary,” where two stars orbit close enough that they share one envelope. This is an extreme case of ellipticity: as the stars orbit, the projected visible surface area changes, affecting the observed brightness.
The second effect is ellipsoidal modulation. A hot Jupiter, being massive and close to its star, can efficiently raise tides on the star. The planet’s strong gravity pulls on the part of the star closest to it, causing the star to lose its sphericity and become somewhat elliptical. This is often seen in close binary star systems, as shown to the right. During an orbit, the observable surface of the star changes in size, causing the observed brightness to change. The magnitude of this effect depends on a planet’s mass, as a more massive planet can induce a larger ellipticity.
The third effect is relativistic Doppler beaming. The Doppler effect, in addition to in(de)creasing the frequency of light as an object moved toward (away) from an observer, also in(de)creases the total observed flux from an object. In a given measure of time, you will encounter more photons from an object moving toward you, as some of them have a smaller distance to travel. You may have empirically observed this while listening to the sound emitted by a train or fast-moving car. Like the previous effect, Doppler beaming depends on the mass of the companion. By observing beaming, we can receive the same information as we would receive from observing the radial velocity wobble of a star, which is simply a different manifestation of the Doppler effect.
The Results
The authors of this paper have developed an analysis package to find and measure these effects. The BEaming, Ellipsoidal, and Reflection (BEER) algorithm has been successfully applied to Kepler data to detect binary stars, while similar methods have been used to find brown dwarfs. For the first time, the authors apply the BEER algorithm to a collection of stars observed by Kepler. One of these, romantically named KIC 4570949, is the subject of this paper. This star was originally misclassified as a binary star system by the Kepler Science Team. After removing the variability in the light curve caused by instrumental effects and the stellar intrinsic variability (mostly caused by starspots rotating into and out of the field of view), the authors found clear evidence for all three effects: the change in flux from the star over an orbit is shown below. As both ellipsoidal modulation and Doppler beaming depend on the planet’s mass, they try to fit each to determine the mass of the planet. Interestingly, from the ellipsoidal motions they measure a mass of 2.1 ± 0.4 Jupiter masses, while the beaming observations are best fit by a mass of 7.2 ± 1.4 Jupiter masses, a difference of 3 standard deviations. Something odd is going on!
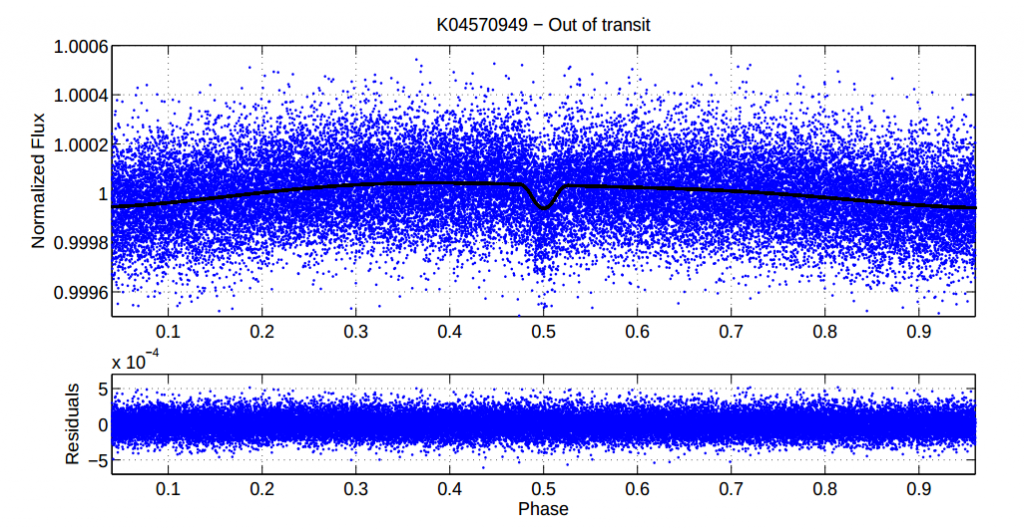
Observed flux from the star KIC 4570949 during one orbit of its planetary companion. A change in flux caused by beaming, ellipsoidal modulation, and reflection can be observed. Also observed is the “secondary eclipse” at a phase of 0.5, when the planet passes behind the star.
To settle this discrepancy, the authors collected 18 radial velocity measurements of this star. This observations are fit to a planetary orbit, and they find a best fit for the planet’s mass of 2.00 ± 0.26 Jupiter masses, consistent with the ellipsoidal observation. Thus, the Doppler beaming measurement is likely in error. To rectify this issue, the authors invoke the idea of superrotation, where a tidally locked planet has an equatorial jet stream moving very quickly and transporting the thermal radiation from a star eastward so that the hottest part of a planet is several degrees of longitude away from the region directly irradiated by the star. Since the BEER reflection signal is presumed to be in phase with the planet’s motion, superrotation will artificially reduce the observed reflected light component and enhance the beaming component. By inserting a superrotation phase shift of 10 degrees into their algorithm, the authors find a new best fit of 2.1 ± 0.4 Jupiter masses, in line with the radial velocity and ellipsoidal observations.
Since radial velocity observations are so time-consuming for faint stars like the ones Kepler observes, techniques to confirm and measure the masses of exoplanets without additional observations are extremely important. Transit timing variations have been successfully applied to multi-planet systems, but studying the out-of-transit stellar flux variations induced by planetary companions will be a very important technique to confirm and characterize hot Jupiter systems uncovered by transit searches, but present and future.



The ellipsoidal effect should go as cos(2phi), which certainly isn’t apparent in the data. It appears that almost all the variation is a straight phase effect. One wonders how many NON-transiting planets are waiting to be discovered in the kepler dataset just from the phase modulation…..
You’re absolutely correct that the ellipsoidal effect goes as cos(2\phi). It’s hard to see by eye in the data because it’s dwarfed by the other effects, but it is certainly found in the data—their model fits it as a 2 M_J planet. Small, and hard to see by eye, but certainly there.
You’re right that the phase modulation is larger for these planets, which is expected. There are several really talented people working to find these non-transiting planets! Like other techniques, this will be most effective for Hot Jupiters due to selection biases, but certainly there will be some of these planets found over the next few years.
I guess I don’t agree that the ellipsoidal (or the photometric beaming effect) are truly detected by the model. being FIT by the model is not the same thing! the cos(2phi) function is definitely NOT seen (above the false alarm probability) in their periodogram. (and of course it should be there at some level as an alias to the orbital period also.). We have it only on the authors’ word that this system would have been found without the very obvious transits (that the Kepler team simply missed, probably bc of the V shaped transit). (yeah, they are good guys, the authors of this paper, the ones I know, but that’s a poor way to do science). IMNSHO opinion this should actually have been been two separate papers, at least. Also note that nothing but the phase effect (plus the super-rotation phase shift, which is obvious to the eye, and which the authors may be mis-interpreting as the doppler beaming) is apparent in the phase binned data, which has incredible precision. Good work, but disingenuous in presentation would be my verdict.