Title: The Analytical Theory of Heat
Author: Joseph Fourier, translated by Alexander Freeman
Status: Published 1822, English translation published 1878 [open access]
Today’s recent astronomy paper is a 200-year-old, 500-page book about heat flow. This arguably stretches the bounds of what’s astrobiteable, even for our Classics section, but I say it counts because a) 200 years ago is recent compared to the age of the Universe, and b) books are printed on paper, so no one can tell me this isn’t a paper.
And if you’re looking for important developments in astronomy, it’s hard to do better than this! It’s the first major work by Joseph Fourier, who made all kinds of important contributions to math, physics, and, strangely, Egyptology. In chapter 4 of this book, he writes down an equation for heat flow that is still the first partial differential equation that most physicists ever learn to analyze. In chapter 3, he straight-up invents Fourier series, which astronomers use to study signals that change over time, from pulsating stars to black holes circling each other.

Figure 1. Mathematicians Adrien-Marie Legendre (left) and Joseph Fourier (right). Legendre, who worked on equations in spherical coordinates, was famously jealous of Fourier’s perfectly spherical head.
But I’m actually going to leave all that, and focus instead on a tiny slice of chapter 2. Four pages, presenting an idea so simple it’s hard to believe anyone had to come up with it. But it’s an idea right at the heart of physics.
“It must now be remarked that every undetermined magnitude or constant has one dimension proper to itself, and that the terms of one and the same equation could not be compared, if they had not the same exponent of dimension.” [emphasis in original]
This idea is the tether between physics and the world it’s meant to explain. Physicists try to describe the behavior of planets and clouds and electrons with pretty mathematical equations. The terms of those equations have to mean something–they have to correspond to the reality that we measure and photograph and weigh.
That means that every physical quantity, every measured thing we label with a symbol and pop into an equation, has, as Fourier says, dimension–the car travels not “100,” but “100 miles per hour;” the vault isn’t “75,” but “75 meters” underground; it contained not “50 million,” but “50 million dollars;” the security camera outage lasted not “4,” but “4 minutes”; I was not “200,” but “200 miles” away at the time, so literally why are you even asking me?
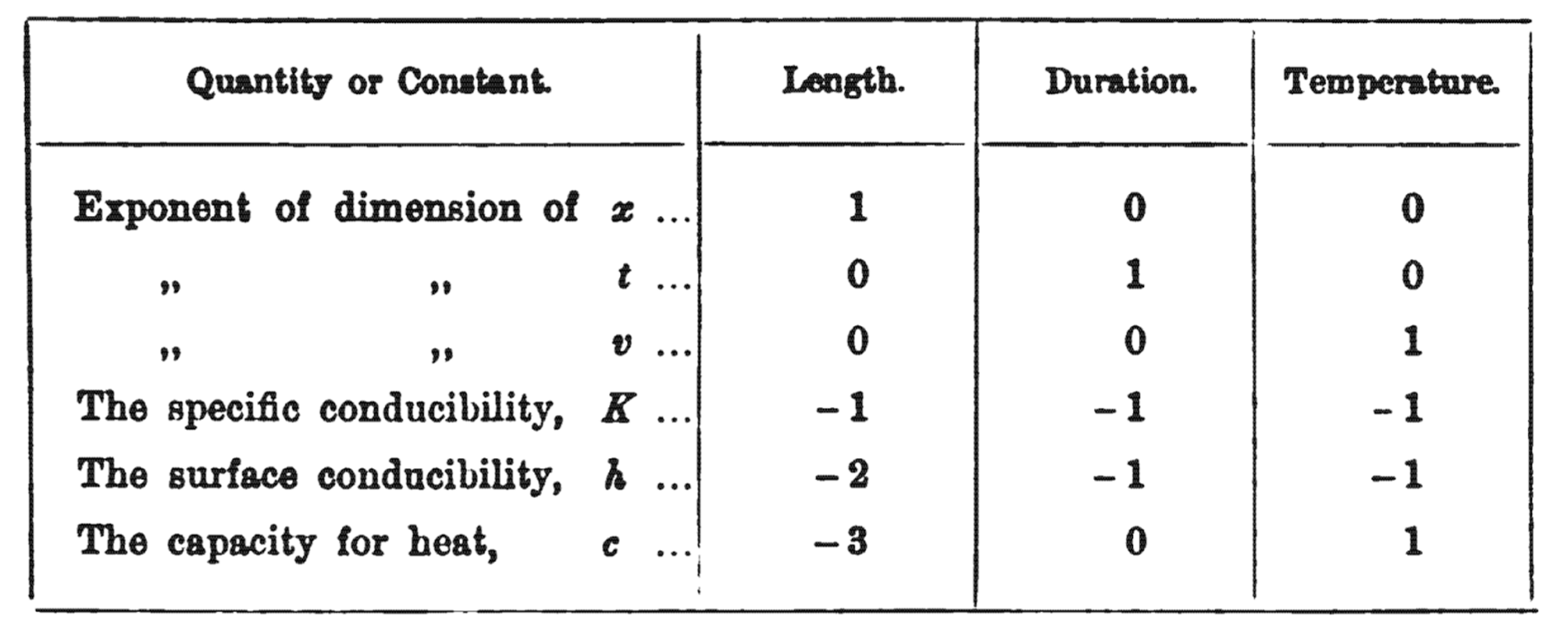
Figure 2. The dimensions of every variable appearing in Fourier’s equation of heat flow. x is a length, so it has units of length^1 × duration^0 × temperature^0. “Surface conducibility” h has units of 1/(length^2 × duration^1 × temperature^1), which makes sense because it describes the amount of heat that flows from a substance per surface area of that substance, per time the heat is flowing, per temperature of the substance.
And since every quantity has a dimension, it only makes sense to compare quantities with the same dimension. The units of the left and right sides of your equation had better match. You can compare lengths to lengths–0.62 miles equals 1 kilometer–but not lengths to times, or masses, or degrees of temperature. I might be of the personal opinion that one dog is greater than a million dollars, but to my ongoing frustration, I can’t express that as a physical law.
This idea of Fourier’s, which we now call dimensional analysis, seems really obvious, but it’s incredibly powerful for a couple of reasons. First, as any physics GRE student can tell you, it’s often possible to estimate the answer to a question by figuring out what units the answer ought to have, and working backwards. For example, say you observe the center of a galaxy varying dramatically in brightness over t seconds, but you can’t resolve it with your telescope and don’t know how big it is. You’re looking for an answer with units of length, so you take your time-scale t and multiply it by the speed of light, which has units of length per time–voila, the maximum length light could have traveled in time t, and therefore the maximum size of your mystery galaxy center. (Anything bigger, and it wouldn’t have had time to change so dramatically in such a short time!)
Second, dimensional analysis means that physical laws are true independently of how humans choose to measure things. We might use kilograms when weighing a boulder, and solar masses when weighing a galaxy, but gravity applies equally to each. The behavior of the Universe as expressed in our equations remains the same, regardless of our arbitrary choices. Good news for those of us who aren’t yet on the metric system!
Featured image by Leo Reynolds, via.



Remember even Sheldon had trouble with the metric system. Embrace the wonderful world of SI.
Many thanks Emily – great post!
And I do recommend metric. It makes life so much easier! (Britain swapped over when I was a young adult and I’m SO GLAD it did!)
I can think in kilometers and kilograms with a little effort! Degrees Celsius is still a challenge, but I’m working on it 🙂
What I found (when moving to Spain) that it’s like learning a new language – you need to begin the think in Celsius!
Have a thermometer registering in Celsius and use that for checking your ambient temperature. Don’t have Fahrenheit on it and don’t translate! After a year of this – that is, winter and summer temperatures – you’ll start to “feel” what Celsius temperatures mean in ordinary life.
It makes Kelvin SO much easier to “grok”.
It’s not units of distance and mass that give trouble, it derived units like force. SI sticks to strict dimensional analysis, which the others do not. Newton II says force =mass times acceleration, giving dimensions of ML/T2. With mass in kg and length in metres this gives the unit of force, the Newton, directly from the dimensions – which the pound foot second system (called Imperial units in Britain) does not.
Emily, an extra sentence in two regarding Why I’m looking for a units in length when looking at the galaxy that varies in brightness would be much appreciated.
You want units of length if you’re interested in estimating the size of the center of the galaxy, assuming that you can’t resolve it with your telescope!
So if I understand this correctly (as a rank amateur who’s unafraid to be in over my head), this measurement would tell me the depth of the galactic center, i.e. as if seen edge-on, as opposed to the width, i.e. in arc-seconds or equivalent fraction of the field of view, as if seen full-face.