Title: Estimating the final spin of a binary black hole coalescence
Authors: Alessandra Buonanno, Lawrence E. Kidder, and Luis Lehner
First Author’s Institution: University of Maryland
Status: Physical Review D, open access
On the fourth of January this year, another gravitational wave signal from the coalesence of two black holes (GW170104) was detected by LIGO. (Read more about the detection here.) Interestingly, the newest detection unveiled clues about the spin of the individual black holes: at least one of the spins was likely in the opposite direction to the orbital motion. The model in this paper gives us insight into the precise way the final black hole spin relates to properties of the individual black holes.
In recent years, numerical simulations have advanced our understanding of the merging of two black holes. However, numerical relativity simulations are computationally demanding and time-intensive, so a simple recipe for computing the properties of the final black hole is very useful! The authors of today’s paper have developed exactly such a recipe from first principles. They assume that the mass and angular momentum of the system are conserved in the merger and ringdown phases, but otherwise make no explicit assumptions from numerical results. The approach is simple yet quite accurate; predictions using this expression are consistent with numerical simulations. The success of this recipe reveals that the fundamental dynamics of binary black hole spacetimes can be encapsulated by quite simple descriptions.
Coalescence of a Black Hole Binary
In this paper, we are discussing Kerr (i.e. rotating) black holes. The angular momentum of each black hole about its own axis is called spin, while the angular momentum of the binary black hole orbit is the orbital angular momentum. You can think of the black holes as a pair of ice skaters that spin about their own axes individually while also circling about a central point. Eventually the two black holes spiral into one another and form a single black hole: this is called the coalescence of a black hole binary.
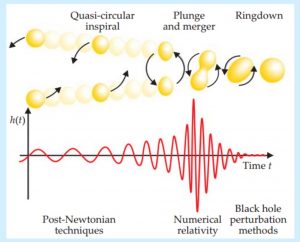
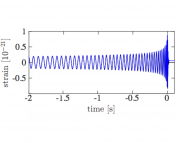
Figure 1: Gravitational wave schematic. (Top) The three phases of coalescence: inspiral, the merger, and the ringdown. (Bottom) The amplitude of the emitted gravitational waves for the coalescence. Source: Baumgarte and Shapiro, 2011.
The stages of the black hole coalescence are depicted in Figure 1. The first stage is the inspiral which consists of a gradually shrinking orbit that is close to adiabatic (i.e. the process is approximately in an equilibrium state at every step). Mainly post-Newtonian methods are used to treat this stage (i.e. Newtonian physics with some modifications to account for relativistic effects). The innermost stable circular orbit (ISCO) is the last complete orbit before the transition to the merger stage in which the two black holes combine into one. The black hole undergoes very complicated dynamics during this stage which can only be dealt with numerically. Immediately following the merger is the ringdown stage in which the now single black hole will “ring” by oscillating in shape. To treat this stage, one has to apply perturbation methods to a single black hole solution. Gravitational wave signals associated with ringdown are discussed in this astrobite.
First Principles Approach
A Kerr black hole can be completely described simply by two parameters, the mass and the spin parameter
where
is the angular momentum of the black hole, due to the no-hair theorem (see this bite). The objective here is to obtain a simple yet accurate “back-of-the-envelope” expression for the angular momentum of the final black hole in terms of the initial parameters of the binary system.
The phenomenological description presented in this paper is motivated by two natural observations about black hole binary evolution: (i) the inspiral evolution is essentially adiabatic, and (ii) the total mass and angular momentum of the system change only slightly throughout the merger and ringdown phases. More specifically, the following assumptions are made:
1. The mass of the system is approximately conserved because the total radiated energy during the merger is small.
2. The contribution to the final total angular momentum due to the individual black hole spins will be approximately determined by the initial spins because radiation falling into the black holes affects the spins by a small amount.
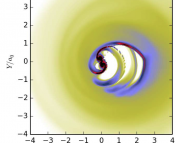
3. To a first approximation, the black hole system only radiates angular momentum during the inspiral phase before the orbit of the binary reaches the inner-most stable circular orbit (ISCO). Once this orbit is reached, the system rapidly moves into the merger phase of its evolution, during which far less orbital angular momentum is radiated. The authors designate the contribution of the orbital angular momentum to the final angular momentum of the black hole to be the orbital angular momentum of a test particle orbiting at the ISCO of a Kerr black hole with the spin parameter of the final black hole (see Figures).
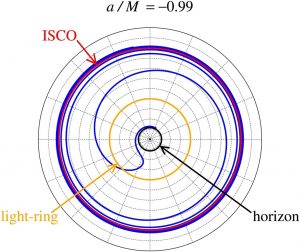
Figure 3: Trajectory of a point mass plunging into a Kerr black hole that is spinning. Source: https://www.aei.mpg.de/1783615/Source_Modeling
Similar approaches in the literature yield the same results for extreme mass-ratio cases. However, crucially, the equation presented in this paper can be used for general mass ratios, including the equal mass case, and encorporates both orbital and individual spin angular momenta in uncovering the final black hole spin. This is significant: in general relativity, solving the two body problem with extreme mass ratios isn’t too difficult (you can use the Schwarzschild solution) but when the masses of the two objects have similar masses, it is a much more difficult problem to solve (generally you need to solve it numerically).
Spin Flip
An interesting example to consider is where the individual black hole spins are not aligned with the initial orbital angular momentum – you can get a “spin flip”!
Firstly, imagine the finely-tuned case where the spin of the final black hole is zero; this scenario emerges where the residual orbital angular momentum at the ISCO is exactly offset by the individual black hole spins (see Figure 5). This critical case is the boundary between cases in which the direction of the final black hole spin is determined by the initial orbital angular momentum, or by the initial individual black hole spins.
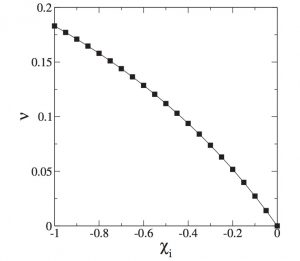
Figure 5: Spins of the black holes to achieve a final non-spinning black hole. is the mass ratio and
for black hole
. Figure 5 in paper.
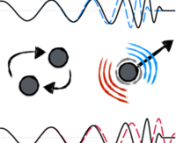
When the orbital angular momentum of the system is not aligned with the individual black hole spins, the final black hole spin can be in a completely different direction to the original individual spins; i.e. when two black holes merge, the spin “flips” (see Figure 4).
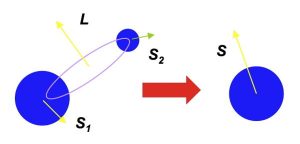
Figure 4: A spin flip. Two black holes with their spins and
in the opposite direction to the orbital angular momentum
of the system coalesce to form a black hole. The final black hole spin
is antialigned with the initial black hole spins. Source: https://briankoberlein.com/2015/04/12/spin-flip/
We can use the expression derived in this paper to uncover configurations likely to yield interesting dynamical behavior, as well as for constructing templates to be used within simulations.

Seems fine but LIGO never detected any gravitational waves in reality. I recently wrote this comment on the romors of neutron star coalescence detected by LIGO as GW; you might find interesting observation in it, coming from somebody outside the formal academic establishment. Most importantly, how did we all assume that GW traveled at c?
Anyway, here is what I wrote: “There might be some astronomical observation of gravitational waves produced by neutron stars; although, I think, this time it is quite improbable, looking at the sheer fortuitousness of the so-called detection makes it untenable — the VIRGO run was too short (just 25 days), LIGO never found any orbiting neutron stars’ gravitational waves in the last 3 years, while there are too many neutron stars nearby to have slipped LIGO’s notice. Let me add, 6 years earlier, minuscule gravitational waves of a wide frequency range (nearly zero to around 3 KHz) were first produced and detected in my lab late in 2010 and were reported in a US patent application which now is a US patent 8521029. You can find the patent detail on the USPTO site as well as on https://www.google.com/patents/US8521029 . You can check out gravitational waves and my work on Wikipedia. Let me also add, even if I am letting out a little secret, it is impossible to register any black hole mergers, because of the sheer volume of mergers — I cannot talk more on this subject. So, let me tell you, LIGO actually never detected any black hole mergers in the past too. The least I can say is that the reported mergers were a result of the intense imagination of the LIGO folks, to say the least. And now to slip in the final secret — Speed of gravity is infinite while LIGO shows it to be equal to the speed of light in its so-called observations. That is why all the gravitational wave observations by LIGO are false.”