Title: An absorption profile centered at 78 megahertz in the sky-averaged spectrum
Authors: Judd Bowman, Alan Rogers, Raul Monsalve, Thomas Mozdzen & Nivedita Mahesh
First Author’s Institution: School of Earth and Space Exploration, Arizona State University, Tempe, Arizona
Status: Published in Nature [closed access]
Today’s astrobite is about the exciting detection of the 21cm neutral hydrogen emission during the Cosmic Dawn, a topic covered many times in the past (for example here, here, here, oh and here). The 21cm emission from neutral hydrogen has the ability to open up secrets of the early universe and give us some keen insight into how the first stars and galaxies formed and how the universe became reionized. You may be familiar with the cosmic microwave background (CMB) which has provided us with evidence for some of our most important cosmological understandings due to measurements by the satellites COBE, WMAP, and Planck. In much the same way the Experiment to Detect the Global Epoch of Reionization Signature or EDGES (Figure 1) has now done the same for the period between recombination and reionization. So now let’s jump into why this detection is so amazing and how there may potentially be some new underlying physics at work.

Figure 1: The Experiment to Detect the Epoch of Reionization Signature (EDGES) single antenna radio telescope. Situated in Western Australia at the Murchison Radio Astronomy Observatory.
The Global 21cm neutral hydrogen emission
To get a good understanding of the detection, let’s break down exactly what constitutes the global 21cm neutral hydrogen signal. The 21cm (1420 MHz) emission occurs from the forbidden spin-flip transition of neutral hydrogen, which gets stretched by cosmological redshift to lengths of meters. We say ‘forbidden’ because the time-scale for the probability of a single hydrogen atom undergoing this transition is on the order of megayears. Luckily when trying to observe this emission we are doing so in bulk, (there is a lot of hydrogen in the universe) so it’s not an impossible task. Another important point is that the neutral hydrogen (and also it’s signal) is strongly coupled to the CMB, for example looking to Figure 2 (bottom), neutral hydrogen and the CMB are at the same temperature everywhere that the differential brightness temperature is zero.
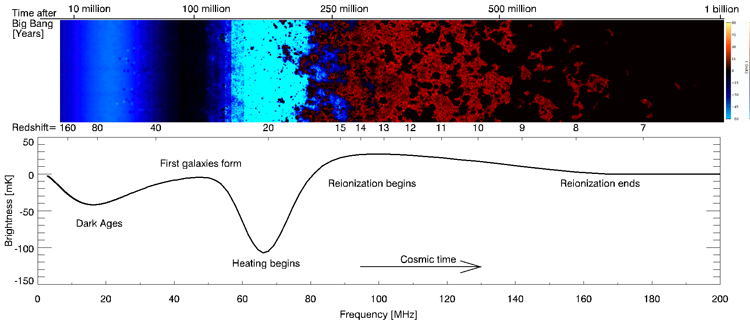
Figure 2: The global 21cm neutral hydrogen signal over redshift (and frequency) where the top image is the spatially fluctuating 21cm neutral hydrogen and the bottom is the globally averaged 21cm signal. The 21cm signal is strongly coupled to the CMB, which means it is undetectable until the temperature of the neutral hydrogen deviates from the CMB. Borrowed from http://pritchardjr.github.io/research.html.
Ok, so now we have some basics down and we know that the global 21cm signal is just the average of the 21cm signal over large scales. Now what exactly do we need to use to detect this global signal? Can we use a radio interferometer (e.g. HERA, MWA, and LOFAR)? Unfortunately not. Radio interferometers are insensitive to the globally averaged signal, and are better suited for trying to detect the spatial fluctuations (Figure 2 top). You therefore need to use a wideband single antenna radio telescope; and you want it to be wideband because the early global 21cm signature occurs over a redshift range of 13 < z < 27 which corresponds to the frequencies of 50 – 100 MHz.
The Detection
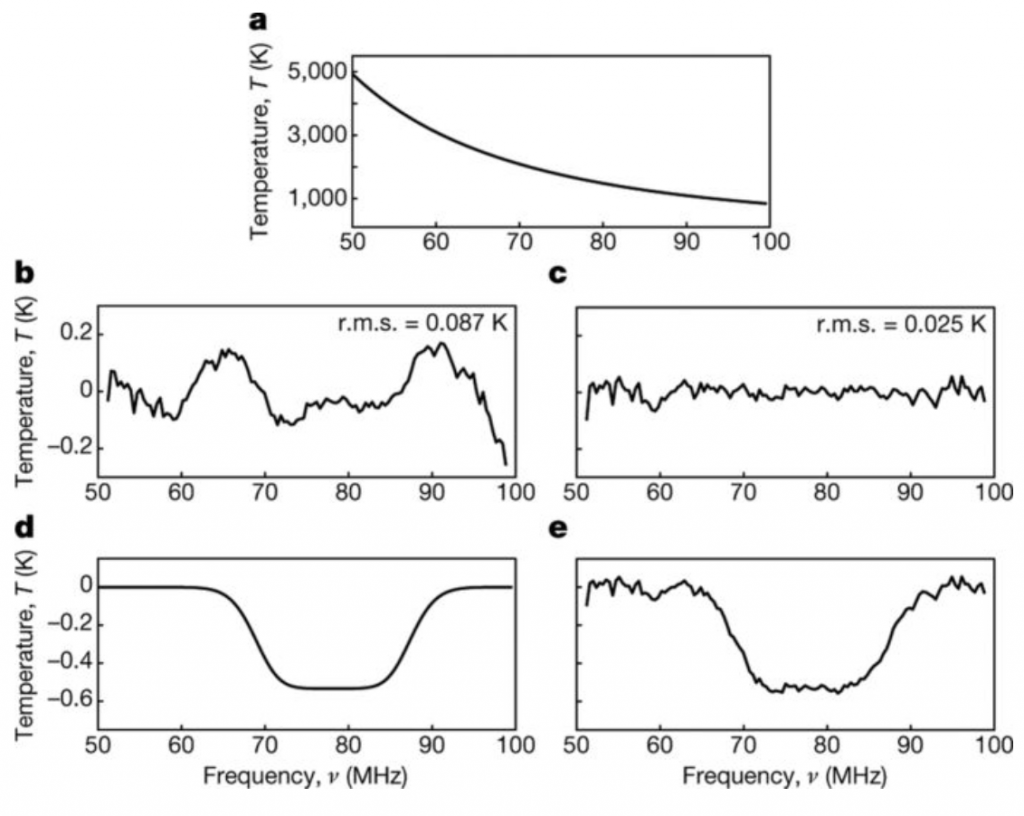
Figure 3: (a) The EDGES sky measurement in units of brightness temperature, showing the strong power-law spectrum due to galactic synchrotron emission. (b) Residuals after removing the power-law dependence. (c) Residuals after removing the power-law synchrotron emissions in addition to a model (d) of the 21cm absorption signal. (e) Residuals from (c) added to model in (d).
The two biggest issues with detecting this faint signal are to do with calibration of the instrument, and galactic synchrotron emission. To try and compensate for introducing false signals added to their measurements due to calibration of the instrument, the author’s separately apply two different calibration techniques. This ensures that a detection seen in one calibrated measurement should be also present in the other differently calibrated measurement. The other problem is due to incredibly bright synchrotron emission, which appears to be almost 4 orders of magnitude larger than the signal! To account for this the authors depend on the fact that these foreground emissions should be smooth over frequency, meaning you can fit and subtract out a low-order polynomial from this measurement and ideally there should be no loss of signal. They fit a 4th-order polynomial and the residuals look like those seen in Figure 3(b). They then simultaneously fit the 4th order polynomial with a model of an expected 21cm signal (for many realizations of a 21cm signal). Their best fit model is demonstrated in Figure 3(d), and the residuals from the combined fit (polynomial + 21cm model) in Figure 3(c). From this measurement they detect an absorption profile centered at 78 MHz (z ~ 17) over 19 MHz with an amplitude of -500 mK. This now leads us to an interesting consequence concerning the amplitude of the absorption, represented by the depth of the troughs in Figures 3(d-e), which is over a factor of 2 larger than originally expected. This is where we can begin to introduce dark matter.
Implications for Dark Matter
Our original understanding of the amplitude for this absorption profile is limited by the minimum temperature of neutral hydrogen that can be achieved by adiabatic cooling due to cosmic expansion. Based on this measurement which appears to be twice as large as expected, we are led to believe there must be an additional mechanism that is cooling the neutral hydrogen below this adiabatic limit (there is another explanation which states that the background radiation temperature could have been hotter but dark matter is more fun). So how does dark matter come into play? In general, for the neutral hydrogen to become cooler it must come into contact with something even colder. This implies that through interactions such as baryons scattering with dark matter particles it can drive down the temperature leading to the larger amplitude absorption profile. These relative scattering velocities also place constraints on important dark matter particle parameters such as the mass and cross-section (check out this primer). By looking at the minimum temperature achieved by cooling from both cosmic expansion and dark matter interactions, theorists (companion dark matter paper released same day) were able to place constraints on both these parameters which give us a cross-section, and a particle mass
, in the ~1 GeV range. Of course all of this should be taken with a healthy skepticism but the idea of using 21cm observations to constrain dark matter is truly promising.
The Future of 21cm Observations
This is most certainly an exciting detection which opens up many more questions than it answers. The next order of business is to confirm the initial detection by EDGES, either by another single antenna global 21cm experiment or by measuring the spatially fluctuating 21cm signal using an interferometer around the same redshift range as EDGES. By getting additional instruments to measure this period, the role of dark matter in cooling baryons in the early universe can either be ruled out or as it appears as of right now provide a useful probe into their detection. Either way, the Cosmic Dawn is hiding many more secrets for us to discover.





10^-21 is not even on the cross section axis of this WIMP graph. So, would that not imply that WIMPs do not exist and can be ruled out from having a role in cooling baryons in the early universe?
I believe this is model dependent as you could probably have some type of multi-component dark matter. Additionally the cross-section measurement used in the Barkana 2018 companion paper assumes a cross-section dependent on the relative velocity as v^-4. They’ve since walked back a bit on their original paper and released a followup (https://arxiv.org/pdf/1803.03091.pdf) outlining how a v^-4 dependence requires a millicharge DM particle. So I would really take the factor of 2 larger absorption profile and the companion DM paper as a proof of concept that 21cm observations can aid in constraining DM.
First starlight implies first galaxies implies galactic magnetic fields… wouldn’t those promote the singlet state and reduce the spin temperature of the HI ?