Title: On the Detection of Exomoons Transiting Isolated Planetary-Mass Objects
Author: Mary Anne Limbach, Johanna M. Vos, Joshua N. Winn, Rene Heller, Jeffrey C. Mason, Adam C. Schneider and Fei Dai
First Author’s Institution: Department of Physics and Astronomy, Texas A&M University, College Station, TX, USA
Status: Accepted to ApJ (open access on arXiv)
When faced with the sheer beauty of shimmering stars emblazoned across a night’s sky, it’s hard not to imagine that there are innumerable other worlds out there — entire planets teeming with alien life, or ruins of once-great civilisations. Until recent decades, such imagination was confined to the realm of science fiction, but in 1992 came the first detection of an exoplanet: a planet outside our solar system.
The study of exoplanets provides important insights into the physics that govern the formation and evolution of planetary systems – in addition to raising many philosophical questions – but exoplanets are notoriously difficult to detect. The primary method of detection relies on measuring the dimming of a parent star during a planetary transit. Even more difficult to detect are exomoons: moons orbiting exoplanets. They are almost impossible to image directly due to the glare of the host star and, due to their smaller size, harder to detect via transit photometry. However, exomoons are believed to be at least as common as exoplanets. The authors of today’s paper point to a source where exomoons may be more easily detected: isolated planetary-mass objects (IPMOs), also known as rogue or nomadic planets.
Sunless Skies
Rogue planets are not bound to a planetary system. Instead, they roam free throughout the galaxy, bathed in darkness and lit by no sun. This makes it much easier to detect exomoons that orbit IPMOs compared to those orbiting ordinary exoplanets. The authors estimate that for over half of all known IPMOs, the sensitivity of the upcoming James Webb Space Telescope (JWST) is enough to detect the presence of an exomoon with similar characteristics to Jupiter’s moon Ganymede. Before planning an exomoon hunt, one must first consider observational constraints. One of the most important is the probability of observing a transit in the first place. Simulations have demonstrated that the formation of moons is common – with at least one large moon forming in roughly 80% of planetary systems – and that these moons often resemble the Galilean moons with respect to their sizes and orbital configurations.
Moonlight Sonata
It is therefore sensible to model probabilities based on moons in our own solar system, such as those orbiting the gas giants. The authors first model the transit probabilities for the solar system gas giant moons – that is, they find the probabilities that a moon will cross the face of the gas giant – with respect to some randomly oriented observer located outside the solar system.
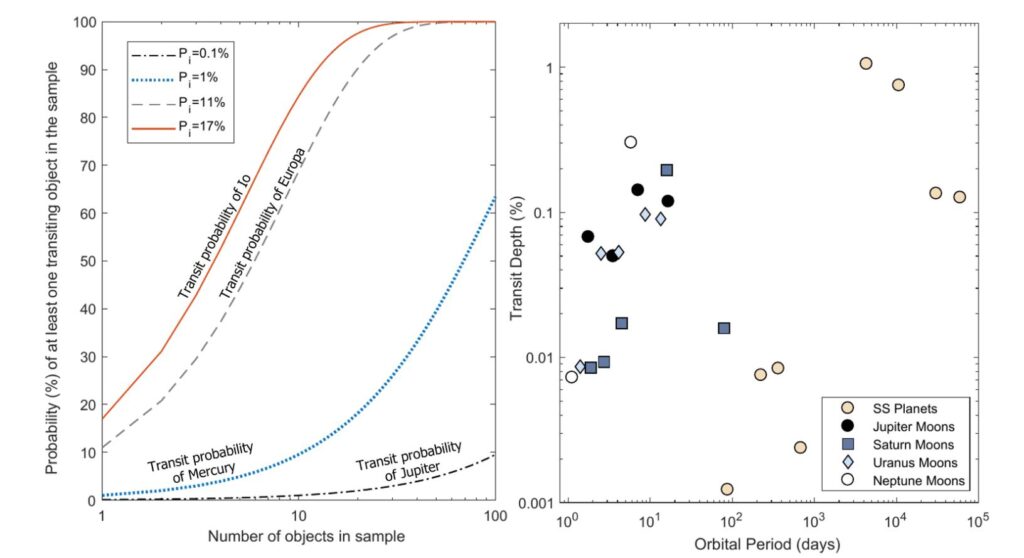
Figure 1 shows the probabilities of observing at least one transit in some system of planets, as well as the observed transit depths. In this case, the transit depth refers to the fractional dip in the light curve of a planet as it is transited by its moon. Supposing that we observed 10 planets with moons, the probability of observing a transit of an Io-like moon is about 85%. For a Europa-like moon, the transit probability drops to 70%, while transits of Mercury-like and Jupiter-like moons are much rarer, at 10% and less than 1% probability respectively.
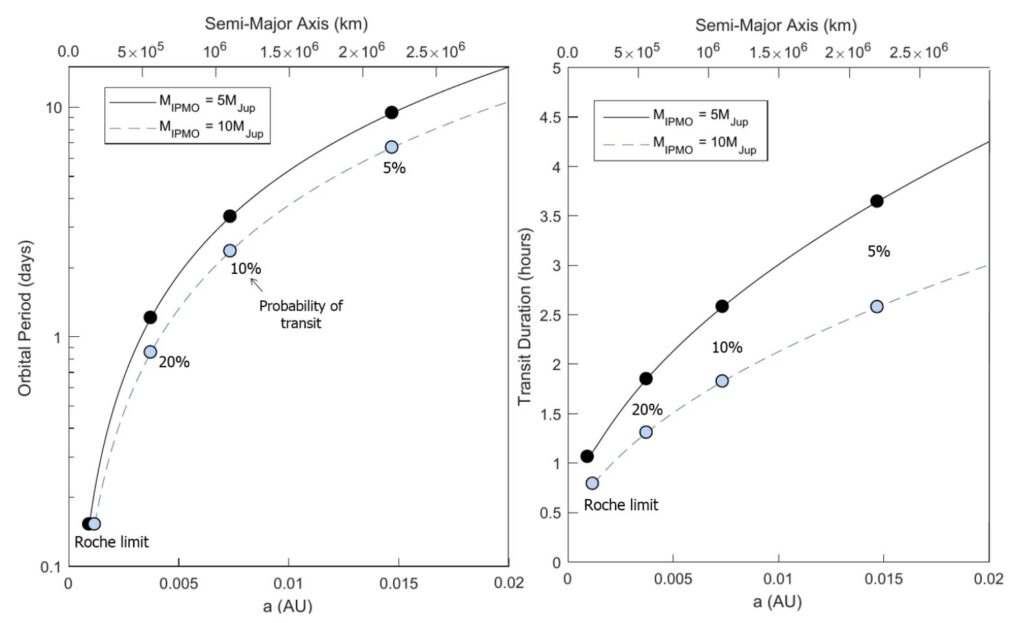
Figure 2 shows the orbital periods and durations of possible transits as functions of orbital radius. In general, the closer the exomoon is to the exoplanet, the more likely it is to observe an exomoon transit. Based on Figure 2, the authors suggest that most exomoons will have a transit probability of 10 to 20%, and that they will likely be detected within a minimum of 50 hours of observation.
Roguelike Exomoons
The main advantage of looking for moons around IPMOs is that high-contrast and high-resolution imaging is not needed; there is no interference from a nearby host star to drown out any signal. Instead, current ground telescopes can observe IPMOs with very high precision. Next-generation space-based telescopes, such as the imminent JWST, will further improve this precision by an order of magnitude.
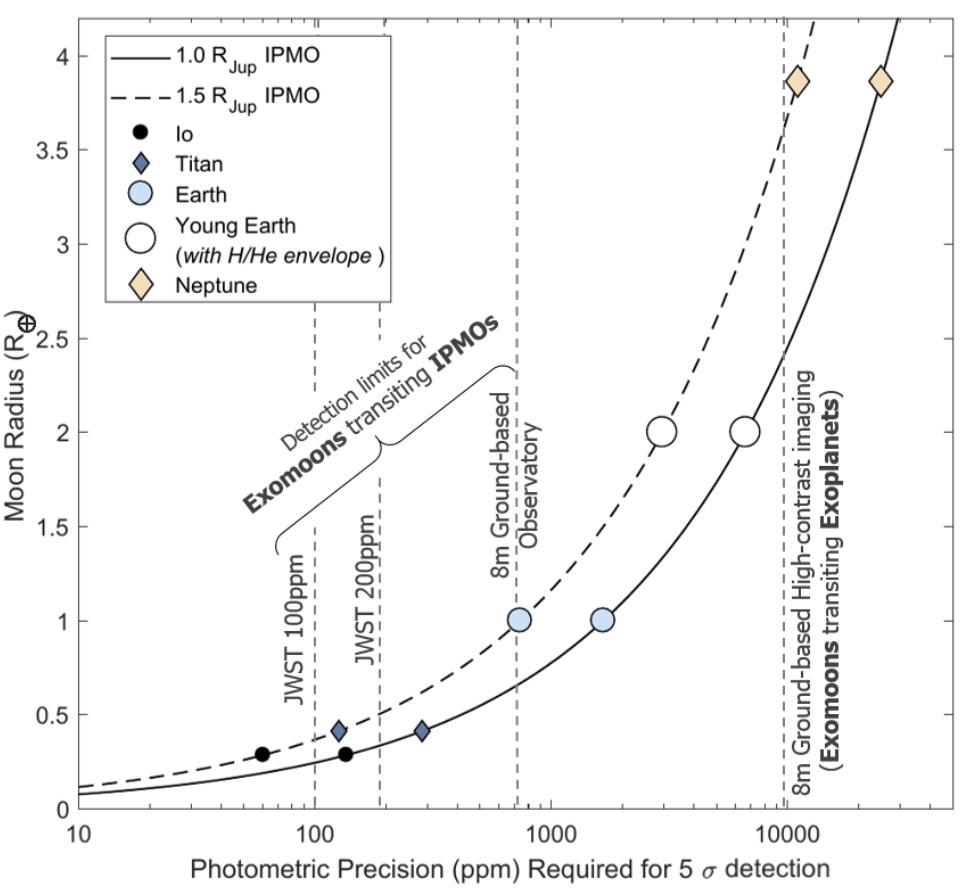
Figure 3 shows the radius of moons orbiting Jupiter-mass exoplanets versus the photometric precision required to accurately detect their transit. Current high-contrast imaging of stellar-bound exoplanets can only detect moons at least as big as Neptune. With IPMOs, ground-based imaging allows for the detection of Earth-sized moons. With the JWST, it will be possible to detect Ganymede-sized moons, and even moons down to the size of Titan or Io! The authors calculate that the JWST will be able to detect Ganymede-sized moons around over half of all known IPMOs.
Sic Mundus Creatus Est
Exomoons are believed to be just as common as exoplanets, with at least one large moon forming around approximately 80% of simulated planets. Rogue exoplanets can be observed with a higher photometric precision since there is no glare/interference from a nearby host star. Moon-planet transits are also relatively common, and more than half of all known IPMOs are bright enough to allow for the detection of a Ganymede-sized moon. However, the authors propose a minimum observing time of 50 hours, which adds up to nearly 17 weeks of combined observing time for the 57 known IPMOs. The authors note that IPMO exomoons are among the most accessible candidates for detecting habitable worlds (in this case, the moon is warmed by tidal heating rather than by a star). Potentially habitable IPMO exomoons would not only lend insight into the processes governing planet formation, but could also offer a window into the conditions of the primordial Earth, thus allowing us to place a timescale on the development of life itself.
Edited by: Ryan Golant
Featured image credit: Mary Anne Limbach