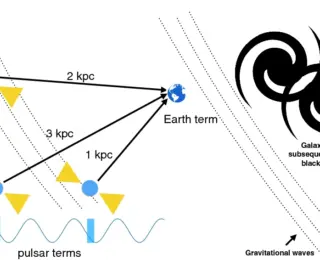
by William Lamb | Feb 26, 2024 | Daily Paper Summaries, PRJ
Pulsar timing arrays could localise individual sources of gravitational waves to host galaxies. The problem is, it’s so computationally difficult! This paper shows us a faster way.
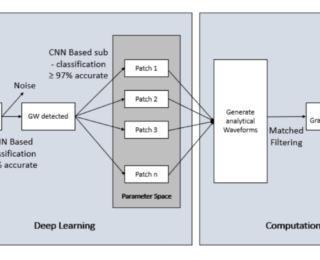
by Guest | Aug 30, 2022 | Daily Paper Summaries
Ever imagined what computers go through while analyzing gravitational wave data? Today’s post sheds light on this computing nightmare.
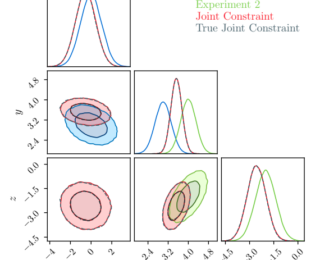
by Guest | Feb 20, 2020 | Daily Paper Summaries
Constraining physical parameters in a cosmological survey is often computationally expensive, especially when considering more than one survey at a time. The authors of this paper offer a simple method to reconstruct parameter distributions in a fraction of the time needed for most high-performance computers.

by Briley Lewis | Feb 25, 2019 | Daily Paper Summaries
Finding craters is a pesky problem – so let’s outsource it to machine learning!

by Ben Montet | Mar 8, 2013 | Daily Paper Summaries
The number of known moons of Pluto has now reached five. What are they like, and how did they get there? Kenyon and Bromley use numerical simulations to answer these questions and determine what else New Horizons may find in 2015.
by Guest | Nov 26, 2011 | Guides
This post is written by Benjamin Nelson, a graduate student in the Astronomy Department at the University of Florida. He works with Dr. Eric Ford on the characterization and dynamical evolution of extrasolar planets. He is currently developing an N-body Markov chain Monte Carlo for RV observations of exoplanet systems. Why is this important to astronomy? Inevitably in your astronomical career, you’ll attend some talk where the speaker mentions “MCMC” and “Metropolis-Hastings”, or maybe something about “priors” and “likelihood functions.” The latter terms refer back to a Bayesian framework, while the former terms are the numerical tools, both of which are rarely covered in undergraduate astronomy/physics. Although Bayes’ theorem has been around for more than 200 years, computational advances within only the past couple decades have made it actually practical to solve problems involving Bayesian techniques. Learning statistical methods is like eating your vegetables: you probably won’t enjoy it, but it’ll be good for you in the long run. It is hardly motivating for an astronomy grad student to pick up an introductory book on Bayesian statistics without some practical application in mind, but a solid knowledge of Bayesian methods is a great way to find common ground in other, unfamiliar astronomical subfields, or even other disciplines of science. The purpose of this astrobite is to familiarize the reader with conventional Bayesian jargon (sugar coated with some astronomy) and lay out the ingredients to code a Markov chain Monte Carlo from scratch. Bayes’ Theorem: In short, Bayes’ theorem allows us to update our knowledge of a model system using new sets of observations. We use this to quantify the...





