Editor: Tanmoy Laskar
Radio Astronomy lyrics
Observable from ground : Yes
Primary observational restrictions : low-frequency cutoff by ionosphere, man-made radio interference.
Observational technique: radio antennae
Contents
- The Radio Band
- Radio Diagnostics
- Effect of the Galaxy
- Radiative Processes
- Observational Techniques
- Existing Facilities
The Radio band
Frequency – 0 to about 1 GHz
Energy – 0 to about 4 μeV per photon
Wavelength – Infinity to about 30 cm
Radio diagnostics
- Galactic – magnetic fields (synchrotron), solar activity (synchrotron), H II regions (bremsstrahlung), planetary nebulae (recombination lines), pulsars (synchrotron)
- Extragalactic – neutral hydrogen content and kinematics (hyperfine transitions), magnetic fields (synchrotron), relativistic electrons (synchrotron), jets (synchrotron), AGN (synchrotron and bremsstrahlung)
Effect of the Galaxy
- Faraday RotationA linearly-polarized wave can be decomposed into a sum of left- and right-circularly polarized waves at the same frequency (with a zero phase difference corresponding to polarization along one of the Cartesian axes). These left and right circularly-polarized components travel at different speeds through a plasma rendered anisotropic due to a magnetic field. Upon exiting the plasma, the left- and right-circular polarization modes have picked up a net phase difference, which causes their sum to still be linearly-polarized, but along a different axis. Thus the plane of linear polarization of an em wave is rotated upon propagation through a magnetized plasma.This effect is frequency-dependent. Our Galaxy is full of ionized hot gas (H II), and is simultaneously permeated by a large-scale magnetic field. The Faraday effect due to this plasma is observed in the polarized signal from radio pulsars within our Galaxy, and on all extragalactic radio sources. How do we know what the original plane of polarization is? We don’t – so the effect is almost always studied as a function of frequency.
- Scintillation Just like stars twinkle due to turbulence in the Earth’s atmosphere, point sources (~ microarcseconds in size) of radio waves such as quasars and interstellar masers twinkle as their radio waves pass through the turbulent interstellar medium on the one hand, and the fluctuating Solar wind within the interplanetary medium, on the other hand. Both these effects, as well as scattering from dust grains in the ISM cause the sources to look larger than they really are. The term coined for this phenomenon in the optical is “seeing” – there is a “seeing” in the radio, too!
- Foreground contamination: synchrotron radiation from Galactic planeOur Galaxy emits bright synchrotron radiation (see below) from relativistic electrons gyrating in the Galactic magnetic field. This emission is strongest in the Galactic plane, where the electron density is the highest. Being a synchrotron spectrum, this radiation is stronger at low frequencies, and completely dominates the radio sky below 100 MHz.

A 22 MHz all-sky map. The dominant source is synchrotron radiation from our Galaxy. This is a foreground that needs to be modeled and removed for any precision radio measurement at low frequencies, such as the CMB (WMAP), and epoch of reionization (LOFAR).
Credit: Giardino et al., A&A 387, 82-97 (2002).
Radiative processes
Paradoxically, some of the most energetic phenomena in the Universe produce copious amounts of the lowest energy electromagnetic radiation – radio waves.
Sources of radio continuum
Continuum, or broad-band sources are visible across the radio spectrum. Increasing the bandwidth of the receiver systems improves the flux measurement of continuum sources. The signal-to-noise ratio for radio observations of continuum sources is proportional to one over the square root of the product of the integration time and the observing bandwidth.
Synchrotron (non-thermal)
Need: relativistic electrons, magnetic fields

Synchrotron radiation from radio galaxy Cygnus A (courtesy: Chris Carilli)
The paths of charged particles are bent by the presence of magnetic fields. As their space velocity changes, they accelerate. All accelerated charged particles radiate. In the case of relativistic particles (usually electrons) spiraling in magnetic fields, the resulting emission is called synchrotron radiation. The total power radiated by a relativistic particle of Lorentz factor, ɣ in a magnetic field, B is proportional to ɣ2B2.
The detailed shape of the spectrum of synchrotron radiation is complicated, but for a power-law distribution of electrons,
N(E) ∝ E-p, the spectrum is also a power law, P(ω) ∝ ω-(p-1)/2. Physical arguments (finite total energy) require that p>1, which means that synchrotron radiation is stronger at lower frequencies.
Suggested Reading:
1. Prof. Malcolm Longair’s Course Notes
2. NRAO Essential Radio Astronomy
Examples: supernova remnants, GRB afterglows, radio galaxies
Diagnostics for: Magnetic field magnitude and direction, relativistic electron population (Number density as a function of electron energy)
Bremsstrahlung (thermal)
Need: free electrons and ions, high density

Overlay of VLA 330 MHz radio contours on a UK Schmidt optical photograph of the Orion region. The radio emission is dominated by thermal bremsstrahlung from hot gas ionized by the central stars of the nebula.
Credit: Subrahmanyan et al., AJ, 407, 121 (2001).
The paths of charged particles are bent by the presence of other charged particles – in particular, the paths of free electrons are bent when they pass by charged ions. As their space velocity changes, they accelerate. All accelerated charged particles radiate. Thus a hot plasma, which has free electrons and ions, is able to cool by free-free- aka bremsstrahlung- (“braking”) radiation. The spectrum of the radiation is calculated by averaging over the impact parameter for all possible trajectories of the electron with respect to the ion followed by an average over the speed distributions of the electrons. The result is different for non-relativistic bremsstrahlung (aka “thermal” bremsstrahlung, with a Maxwell-Boltzmann speed distribution assumed), and bremsstrahlung from relativistic particles1 (non-thermal free-free emission)
Thus thermal bremsstrahlung is observed for any source consisting of hot plasma. The free-free emissivity scales as the square of the density, and is dominant over non-thermal (synchrotron processes) in hot, dense gas with weak magnetic fields.
Suggested Reading:
1. Prof. Malcolm Longair’s Course Notes
2. NRAO Essential Radio Astronomy
Examples: H II regions, pulsar wind nebulae
Diagnostics for: Electron temperature and density
1 Credit: Dr Martin Kohl
Sources of radio spectral lines
Radio spectral lines only appear at frequencies characteristic of the atomic transition responsible. The signal-to-noise ratio of spectral line observations is independent of the bandwidth, but is still inversely proportional to the square root of the integration time.
Recombination lines (thermal/non-thermal)
Need: partly-ionized medium
The frequency of an atomic transition from an upper level, m to a lower level, n is given by the Rydberg formula, When m = n+1, the line is designated as an nα transition, while for m = n+2, m = n+3, … we have an nβ, nγ … transition. For large n and m, these frequencies fall in the radio wavebands. An analysis of the relative intensities of observed radio recombination lines yields a direct measure of the electron temperature in the source region, as well as abundances of the emitting species (just as in the optical bands).
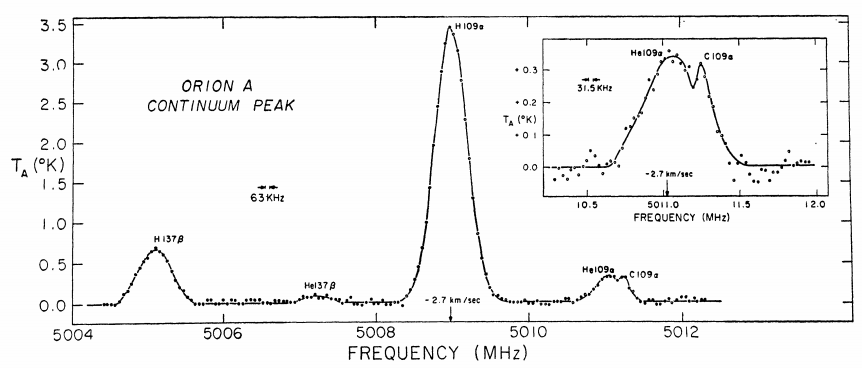
Radio (pushing microwave) recombination lines from the star-forming region, Orion A. The booming central line is H109α, i.e. a transition between a principal quantum number from 110 to 109. Recombination lines from other species, as well as other high-n transitions of Hydrogen are visible in the same spectrum.
Credit: Churchwell and Mezger., Ap. Lett., 5, 227 (1970).
Examples: H II regions, planetary nebulae, nuclei of radio galaxies, hot gas in the ISM
Diagnostics for: Ionizing photon flux, electron temperature, electron density, emission measure (integral of the square of the electron density along the line of sight)
Suggested Reading:
1. Review article by Dupree and Goldberg (1970)
2. Review article by Brown et al. (1978)
3. NRAO Essential Radio Astronomy
Hyperfine structure (thermal)
Need: neutral hydrogen *

The H I Nearby Galaxy Survey (THINGS)
In atomic hydrogen, the ground state (n = 1) state is split by coupling of the electron spin to the magnetic dipole moment of the nucleus. When the spins of the proton and electron point in the same direction, the system has a slightly higher energy (about 6 x 10-6 eV) than when the spins are anti-aligned. Transitions between the two states lead to the emission of a hyperfine line at 21 cm. The probability of any given hydrogen atom making this transition is exceedingly small (the lifetime of the upper state is 107 years), but there is so much neutral hydrogen in the universe that this transition is almost ubiquitous.
* Hyperfine transitions in other species, such as deuterium and 3He+ can also be observed.
Examples: Diffuse ISM of other galaxies, ISM of the Galaxy, neutral intergalactic medium (at z > zreionization)
Diagnostics for: Kinematics (rotation curves), total gas mass
Suggested Reading:
1. The HI Nearby Galaxy Survey (THINGS)
2. NRAO Essential Radio Astronomy
Observational techniques (Radio Antennae)
Elements of a radio telescope
1. Reflective element (e.g. parabolic dish)
The reflective element focuses parallel beams of radio waves on to the active element at the focus. It also shields the feed from radiation from the ground and surroundings. The reflective element determines the shape of the primary beam of the telescope (e.g. the beam pattern of a paraboloidal dish antenna on the sky is the Airy pattern) and sets the basic restrictions on the required pointing accuracy of the telescope.
2. Active element (aka “feed”: e.g. dipole or horn antenna)
The feed is an example of a transducer – it captures radio waves traveling through the air and transforms them into electric signals on a cable.
3. Radiometer (Receiver)
The receiver is an electronics system that records the power output of the antenna, either by squaring and averaging the signal for some integration time (total power mode) or by cross-correlating signals between multiple antenna (interferometric mode).
It is very common to cross-correlate signals from different antennae, and to use the resulting interference pattern for making high-resolution images. This technique is called “aperture synthesis” or “synthesis imaging”.
Existing facilities
Single Dish: Arecibo (Puerto Rico), GBT (West Virginia, USA), Parkes (Australia)
Interferometers: ATCA (Australia), CARMA (USA), GMRT (India), WSRT, VLA (USA), VLBA (USA)

