Title: CFHTLenS: Combined probe cosmological model comparison using 2D weak gravitational lensing
Authors: Martin Kilbinger, Liping Fu, Catherine Heymans, Fergus Simpson, Jonathan Benjamin, Thomas Erben, Joachim Harnois-D´eraps, Henk Hoekstra, Hendrik Hildebrandt, Thomas D. Kitching, Yannick Mellier, Lance Miller, Ludovic Van Waerbeke, Karim Benabed, Christopher Bonnett, Jean Coupon, Michael J. Hudson, Konrad Kuijken, Barnaby Rowe, Tim Schrabback, Elisabetta Semboloni, Sanaz Vafaei, Malin Velander
1st author’s home institution: CEA/Irfu/SAp Saclay, Laboratoire AIM, France; Excellence Cluster Universe, Boltzmannstr.; Universitats-Sternwarte Munchen; Institut d’Astrophysique de Paris
The Canada-France Hawaii Telescope weak lensing survey, CFHTLens, recently released several papers to help pinpoint the cosmological model that best describes our Universe. If you’re an avid Astrobites reader, you may have seen Chris‘s recent post about the final results from WMAP and wonder, why do we need another method to measure cosmological parameters? As you can see in that post, no one method can measure all the parameters that go into our cosmological model; instead, we must combine multiple methods that have different strengths and weaknesses.
Ultimately, weak gravitational lensing will be a powerful way to get at the nature of dark energy, the mysterious negative pressure causing the Universe to expand at a faster and faster rate. Weak gravitational lensing, which I mentioned last month in an overview of gravitational lensing, lets us map out where mass of all kinds, including dark matter, lies in the Universe. The presence of mass curves spacetime and bends the path of light as a result. Therefore, the images of distant galaxies will undergo tiny (weak) shape distortions as the travel through a network of overdense and underdense regions, such as the large scale structure shown in Figure 1, on their way to us, the observers. This “cosmic shear” stretches or shrinks images of galaxies, in distortions called E-modes (Figure 2). These are the only shape distortions we expect to see. Because background galaxies have their own intrinsic shapes, astronomers must measure the shapes of many, many galaxies with extreme precision to see the effects of weak lensing: these authors use 4.2 million of them!
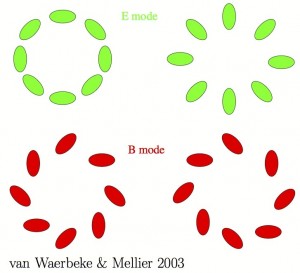
Figure 2: E- and B-mode shape distortions. The left E-mode shows the distortion from an overdensity; the right E-mode shows a distortion from an underdensity. Weak lensing will not produce B-modes.
The easiest thing to do with the CFHTLens data is to make a 2-D map of the projected mass overdensity in that region of the sky, and Elisabeth covered just that in a post a few months ago. But we want to do more than look at this map; we want to study its statistical properties to say something quantitative about how easily structures formed and why. The amount of material bound up in galaxies, galaxy clusters and even larger structures is intricately linked to the expansion rate of the Universe and thus to dark energy as well: gravity pulls matter together, while the expanding universe impedes structure formation by stretching out space itself. The authors measure the strength of the expected shape distortion (E-mode) on many length scales. As a check, they also measure the strength of the B-mode – the shape distortions not expected from lensing – and find it consistent with zero.
The authors are best able to measure a combination of two cosmological parameters: ΩM and σ8. In other words, ΩM tells us how much mass there is overall, while σ8 tells us how that mass has clumped together into cluster-sized structures. Relating overdensities at given angular separations to σ8 requires an assumption of cosmology, since the expansion rate determines the relationship between redshift, our proxy for distance, and true distance from us.
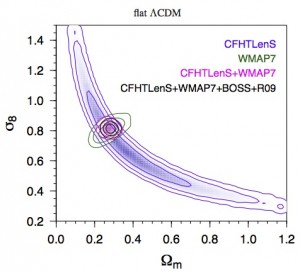
Figure 3: Allowed cosmological parameter values for a flat Universe. The blue "banana" shows the constraints from only CFHTLens data; the other colors add constraints from WMAP (the cosmic microwave background), BOSS (baryon acoustic oscillations), and Riess et al. 2009 (type 1a supernovae).
The authors start with a simple model of the Universe, then experiment with other geometries and relations between dark energy pressure and density. Combining their results with those of WMAP7, BOSS, and type 1a supernovae studies, they use Bayesian statistics to determine which of these cosmologies fits best. Bayesian statistics operate on the principle of Occam’s razor, i.e., the simplest explanation is most likely correct. Here, it means that the model which requires the least fine-tuning of unknown parameters to reproduce the data is the best one. They find that their preferred fit agrees with the standard model, a flat geometry with ΩM=0.23 and σ8=0.87 – all is well in cosmology!
This paper is only the tip of the iceberg for weak lensing cosmology, however. Ultimately, we want to measure mass overdensities on all scales, not just the length scale probed by σ8. We would also like to separate out lensed pairs by their distance from us, which would allow astronomers to create a 3-D map of the structure of the Universe, effectively tracking how it forms over time (since as we look farther away, we look farther into the past). Some companion papers start to do this at the expense of lower signal-to-noise, but ultimately, the strength of weak lensing will present itself when future surveys like Euclid and the LSST arrive.





Trackbacks/Pingbacks