- Title: Planetary System Disruption by Galactic Perturbations to Wide Binary Stars
- Authors: Nathan A. Kaib, Sean N. Raymond, Martin Duncan
- First Author’s Institution: Queen’s University, Kingston, Ontario, Canada
The Hypothesis
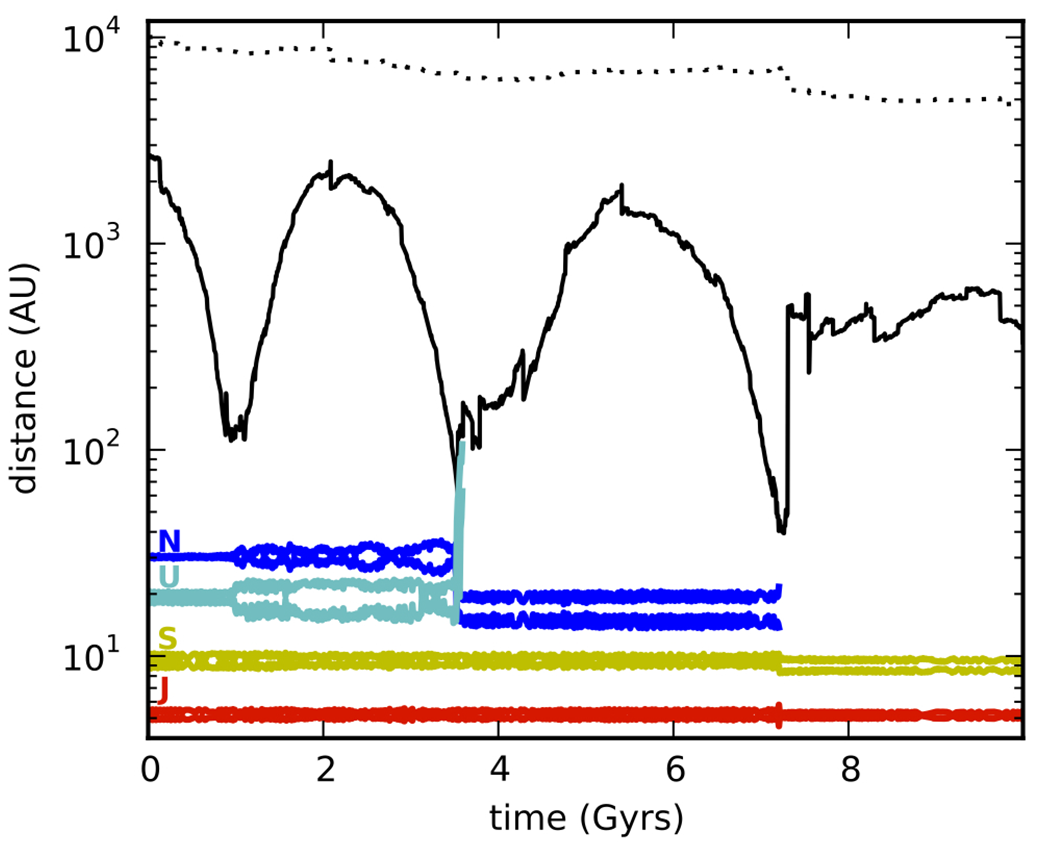
Figure 1: Results of the authors’ simulation of a wide binary companion to the solar system. The colored lines illustrate the orbits of the four giant planets over time (the two lines are the pericenter and apocenter; close-together lines mean the orbit is circular, spread apart lines mean the orbit is eccentric). The dotted black line is the semi-major axis of the companion star, and the solid black line is its pericenter. The companion makes three close approaches to the sun and planets. First, it increases the eccentricity of Uranus and Neptune’s orbits; second, it changes Neptune’s orbit and ejects Uranus completely; finally, it ejects Neptune as well. From Figure 1 of the paper.
Many stars are found in pairs called binary systems, in which the stars are gravitationally bound and orbiting their common center of mass. These systems come in a range of sizes; the stars may be so close together that matter flows between them, or thousands of AU apart. (1 AU is the distance between the Earth and Sun.)
How do planets fare in such stellar systems? Many planets have already been discovered in binary systems, most orbiting only one of the stars, but some circumbinary planets have been found as well. In many binary systems, the combined gravity from both stars allows for stable planetary orbits only in certain regions of the system.
One might think that planets in a very wide binary system would be unaffected by their star’s far away companion. But because the two stars are only loosely gravitationally bound, the companion star will be more easily perturbed by forces outside the system – other nearby stars or even the tide of the galaxy. This could put the companion star on an eccentric orbit, occasionally sending it much closer to the primary star (and to the planetary system) similar to how long-period comets approach the sun from the Oort cloud. How likely is this to occur, and what effect would it have on planets? That is what the authors of this paper seek to explore.
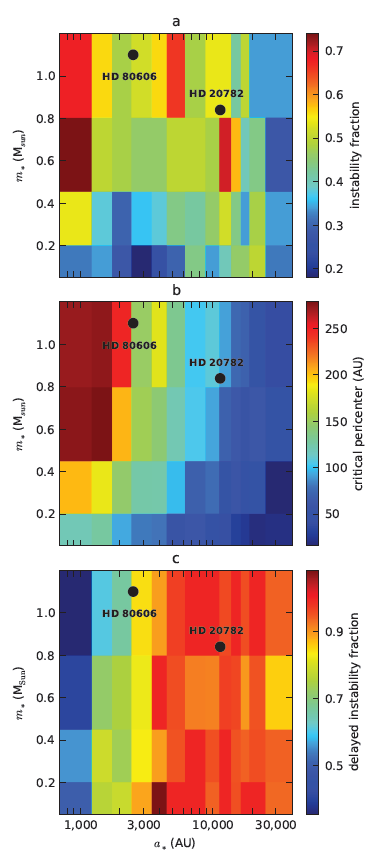
Figure 2: Each panel represents the phase space of initial conditions for the ensemble of simulations. The x-axis is the binary semi-major axis, and the y-axis is the binary star mass. Each panel is colored according to the results of the simulations, with the meaning of the colors varying between the three panels. The black points correspond to two observed binary systems known to have planets. The color in the top panel denotes the fraction of simulations in which at least one planet was ejected. The color in the middle panel represents how near the companion needs to get to the sun to disrupt the planetary system. The color in the bottom panel shows the fraction of simulations in which the instability in the planetary system occurred after at least 100 Myr had passed. From Figure 2 of the paper.
A Test Simulation
The authors test their hypothesis with computer simulations that model the sun and the solar system’s four giant planets, but also add a companion star on a wide orbit. They model the gravitational effects between these objects and mimic the influences of the galactic tide and nearby stars on the companion star. (The title of this post would be more accurate to reference “pulling” instead of “pushing”, as gravity is a purely attractive force.)
The results of one of their simulations are shown in Figure 1, illustrating how the orbits of the planets and companion star change with time. The dotted line is the companion star’s semi-major axis, representing the overall size of its orbit. While this decreases somewhat over time, the companion remains a very wide binary throughout the simulation. The solid black line is the companion’s pericenter (the closest it gets to the sun during its orbit). Initially, the pericenter is 3,000 AU, far enough away to leave the sun and planets in peace, but the pericenter dips three times throughout the simulation, bringing the companion within 100 AU of the sun.
The orbit of each planet is illustrated by two lines of the same color, representing its pericenter and apocenter (the farthest the planet gets from the sun). The farther the two lines are apart, the more eccentric is the orbit. The planets all start on very circular orbits, but during the companion’s first close approach at 1 Gyr into the simulation, Uranus and Neptune are perturbed into more eccentric orbits. At 3.7 Gyr, the companion’s second close approach ejects Uranus from the solar system, and scatters Neptune onto a smaller orbit. Then, on its last close approach at 7.2 Gyrs, the companion also ejects Neptune. Clearly, the wide binary had a significant effect on the planets, although it does not eject a planet until nearly 4 Gyr into the simulation (the age of the solar system is less than 5 Gyr).
An Ensemble of Simulations
Next, the authors run this simulation with a range of initial conditions to test how commonly planets are ejected by a wide binary. The results are presented in Figure 2. Each panel in this figure represents the phase space of initial conditions. The x-axis is the binary semi-major axis, and the y-axis is the companion star’s mass. Each panel is colored according to the results of the simulations, with the meaning of the colors varying between the three panels. The black points correspond to two observed binary systems known to have planets.
The color in the top panel denotes the fraction of simulations in which at least one planet was ejected. Apparently, planet ejection by wide binaries is fairly common, occurring in 30 to 60% of the simulations, and more massive companions are more disruptive to planetary systems. But the size of the binary orbit does not strongly determine the lethality of the companion, because, as the authors explain, while wider binaries are more easily thrown to small pericenters by outside influences, closer binaries orbit much faster, achieving their pericenter distance much more often. These two effects roughly balance.
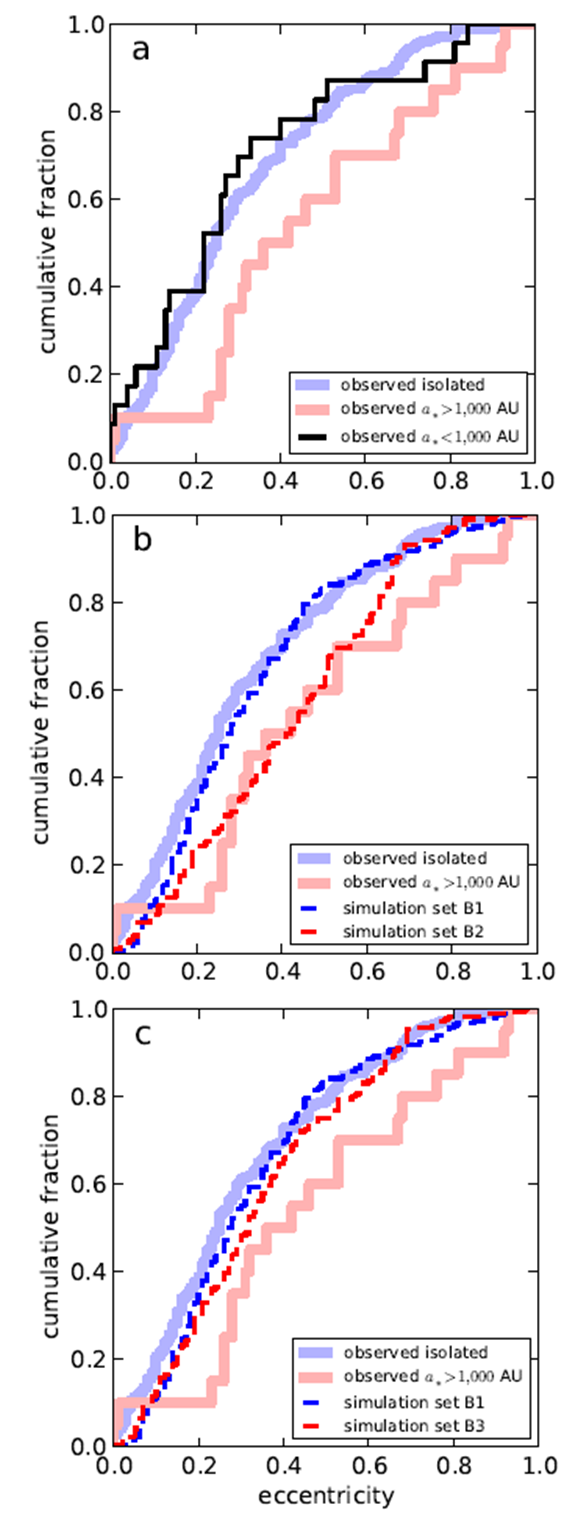
Figure 3: The cumulative distribution of observed and simulated exoplanet eccentricities. The first panel compares observed exoplanets in wide binary (red), close binary (black), and isolated stellar systems (blue). The second panel adds the results from simulated exoplanets in isolated (dashed blue) and wide-binary (dashed red) systems. The third panel is identical to the second, except that the wide binary simulation does not include external forces from nearby stars or galactic tides. From Figure 3 of the paper.
In the middle panel, the color represents how near the companion needs to get to the sun to disrupt the planetary system. The results further emphasize the conclusion that wider binaries need to reach a smaller pericenter than closer binaries to disrupt the planets because closer binaries achieve their pericenter distance more often. (Note that the “closer” binaries tested in these simulations would still be considered wide binaries in the grander scheme). Also, as one would expect, more massive companions can influence planets from a greater distance.
In the bottom panel, the color shows the fraction of simulations in which the instability in the planetary system occurs after at least 100 Myr has passed. In agreement with the test case illustrated in Figure 1, this process is, in general, very delayed, often leaving the planets untouched for hundreds of millions of years (planets form in less than 10 Myr). Only for binaries with semi-major axes less than 2,000 AU are a significant fraction of planetary systems disrupted early.
Comparing with Observations
From Figure 1, we see that wide binaries can leave planets on eccentric orbits (planets are thought to form on circular orbits). The authors examine the eccentricities of discovered gas-giant exoplanets, both in binary and isolated stellar systems, and plot their cumulative distributions in Figure 3. The first panel shows that planets in wide binary systems (red line) are generally more eccentric than planets around isolated stars (blue line) or close binary systems (black line), suggesting that wide-orbit binaries play a special role in exciting planets to eccentric orbits.
The second panel in Figure 3 again shows the eccentricities of discovered planets around isolated stars and stars in wide-binaries, but also the distribution of eccentricities of planets from two ensembles of simulations that were identical except that one had a wide binary companion (red dashed line) and the other did not (blue dashed line). There is a good match between observations and simulations, suggesting that this phenomenon does, in fact, contribute to the eccentricity of planets in wide-binary systems. The eccentricity of planets around isolated stars is due to interactions among the planets themselves.
Finally, the authors rerun the same sets of simulations, but turn off the external influences on the wide binaries. The new results are shown as the red dashed line in the third panel in Figure 3, which more closely matches the eccentricities of planets around isolated stars. This confirms that the presence of a wide binary companion is not enough to match the data, but that external influences from nearby stars and the galactic tide are also required.
Conclusions
The authors of this paper take a second look at a commonly held assumption: wide stellar binaries probably don’t affect planetary systems. They expand the scope of the problem to consider the influences from outside the stellar system, and find, via detailed simulations, that wide binaries can perturb planetary systems, perhaps even more so than closer binaries. They show that this previously-unconsidered mechanism can explain the observed eccentricities of planets in wide binary systems.




Trackbacks/Pingbacks