TITLE: Triple-Star Candidates Among the Kepler Binaries
AUTHORS: Saul Rappaport, Katherine Deck, Alan Levine, Tamas Borkovits, Josh Carter, I. El Mellah, Roberto Sanchis Ojeda, & Belinda Kalomeni.
FIRST AUTHOR’S INSTITUTION: Massachusetts Institute of Technology

An schematic of a tertiary star system. An observer located along the pictured line of sight would observe the binary pair to eclipse during their orbit, while the third star orbited the center of mass of the system, interacting with the eclipsing pair. Credit: Karen Teramura (UH Institute for Astronomy) with background photograph by Wei-Hao Wang.
Binary star systems, in addition to being awesome, are an astrophysically important class of object. Binaries are one of the only ways we can recover dynamical masses of stars and are the baseline to which stellar models are calibrated. We’ve given them a lot of press lately, specifically with respect to planetary systems. However, as much as binaries have taught us about stellar structure and evolution, there’s a lot we still don’t understand about these systems. Many binaries are in extremely compact orbits: some have orbital periods of only hours. How these ultracompact systems form is a bit of an open question. Astronomers know these stars could not have formed in such a tight configuration. Young stars contract from very large gas clouds; during the “protostar” phase, as these stars are heating up and contracting, protostars in a binary system would have been larger than the current orbits of the stars! Therefore, they must have started in wider orbits which became more compact in time. We also know very little about the occurrence rate of triple (and higher multiple) systems in the galaxy. Triple stars in systems may be responsible for driving a pair of bodies into a compact pair. Significantly, triple system occurrence has not been systematically explored by searching for additional companions over a large sample of binary stars.
Kepler, a telescope you may have heard some things about, has been on the case for almost four years. The Kepler science team has developed a catalog of more than 2,000 eclipsing binaries in the Kepler field, and these systems have been observed every half-hour nearly continuously since March 2009. An eclipsing binary that is not a part of a triple system will have an orbital period that does not change in time; the eclipses will occur once per period, at extremely regular intervals. However, if the binary star is being orbited by a more distant companion, two effects will cause the period of observed eclipses to change in time. First, as the tertiary companion completes its orbit, the observed eclipsing binary orbits the changing center of mass of the system, slowly increasing and decreasing its distance from us. The observed eclipses then occur later and earlier (respectively) as the light travel time to the system changes during the orbit. Additionally, small gravitational interactions between eclipsing pair and the tertiary companion can create a small “forced eccentricity” (an eccentricity caused by interactions between bodies) in the eclipsing system, causing the period of the orbit (and the times of the eclipse) to modulate slightly over the period of the outer companion. Thus, by looking for eclipse timing variations (ETVs), one can infer the presence of nontransiting companions. This is very similar to studying planet transit timing variations to look for nontransiting planetary companions.
The authors of this paper attempt to look for these two effects in a search for ETVs in binary stars: for each eclipsing binary star, they fit a model to each individual transit to attempt to find the time of each transit. They then look for departures from an exact periodicity in the observed stellar orbits and try to fit these deviations to the two effects described in the previous paragraph to learn about the parameters of the tertiary companion. This group found a total of 39 likely triple systems through ETVs. A plot showing a few examples of this is shown below.
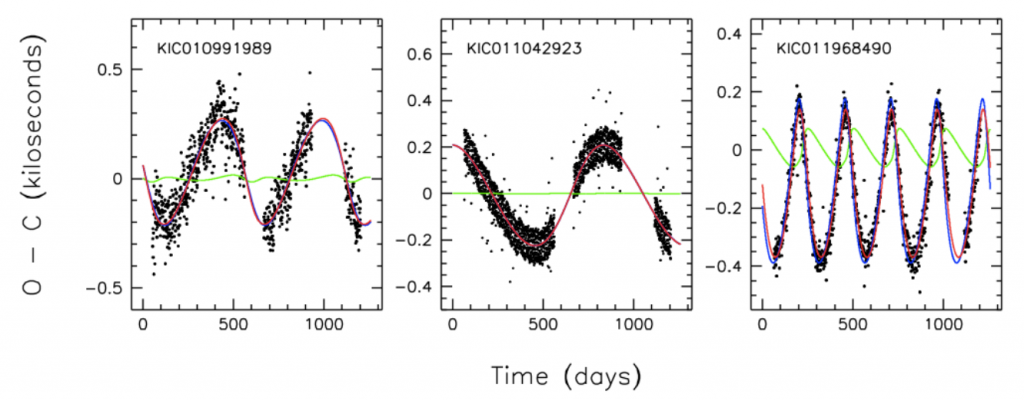
Observed deviations from a calculated linear eclipse timing model (the difference between the observed eclipse times and what would be expected from an exact periodicity) for several eclipsing binaries in the Kepler field. The red curve is the modeled total expected delay. In blue is the expected effect from the light travel time, and the green is the physical delay from multi-body interactions. The period of the signal is equal to the period of the outer companion; the amplitude depends on the mass of the third body. (Figure 5 from Rappaport et al.)
The 39 observed systems each have a candidate third companion, so the authors attempt some statistical analyses of this population. They find that the period distribution for tertiaries is approximately flat in log space (meaning there are equal numbers of tertiary companions with periods between 100 and 200 days as between 200 and 400 days and 400 and 800 days). Moreover, they attempt a crude estimate of the total occurrence rate of tertiary systems. They estimate that they are sensitive to potential tertiary companions around approximately 50 percent of all stars in their sample. With 39 detections around 1000 stars, they thus estimate that 4 percent of binaries have a tertiary companion within a 900-day orbit. At periods longer than this, the authors would not observe a full cycle of ETVs (which have a period equal to that of the third body’s orbit), making the system much harder to characterize. The amplitude of the signal depends on the mass of the third body; the authors suggest they would be able to detect essentially all stellar mass companions in this period range. Nevertheless, the authors claim tentative detections of an additional 40 objects, with only part of the ETV cycle observed. To observe some of this cycle, the authors note the third companion would have to have a period less than 2500 days; they then estimate a tertiary occurrence rate of approximately 8 percent for systems with periods less than 7 years.
To fully complete this study, Rappaport et al. note they would like follow up Doppler spectroscopy of these systems. This will allow for measurements of the masses of each body in the system, as well as better constraints on the orbital parameters of the discovered systems. Once these measurements are collected, this group will be able to perform a careful statistical study of triple systems as a class of objects, paving the way for extensive studies of the formation and evolution of multiple-star systems, both observationally and theoretically. These future studies are of great interest! They will teach us about interactions in multi-body systems and improve our understanding of the formation of compact binaries, which are responsible for much of our understanding about the masses and structure of stars.


typo: you say “stellar mass planets” where I suspect you meant “stellar mass stars”.
Of course! I actually meant stellar mass companions—they’re sensitive to basically all stars (and in special cases should be sensitive to brown dwarfs, although that’s not addressed in the paper). Good eye!