- Title: Formation of Giant Planets by Disk Instability on Wide Orbits Around Protostars with Varied Masses
- Author: Alan Boss
- Author’s Institution: Carnegie Institution of Washington
The modern understanding of planetary formation starts with a gaseous disk swirling around a new protostar. This disk is formed as a way to conserve the angular momentum of the initial collapsing gas cloud that gave rise to the star-disk system. Planets are then thought to form out of the disk and, in the process, clear out much of the initial disk material.
Broadly speaking, there are two main ways that protoplanets are thought to form. The first involves core accretion, where an initial core formed through a hierarchical process of smaller bodies colliding and sticking together (this process is reasonably well understood at the sub-centimeter level, but it is not yet clear how this precisely works when talking about, for example, kilometer-size objects). This core then reaches some critical mass after which it begins to accrete gas from the disk. Eventually the core opens a “gap” in the disk, which slows the growth of the protoplanet.
The main alternative to the core-accretion model is the hypothesis that planets might form through global gravitational instabilities in the disk. The basic idea is that when a disk is massive enough to experience significant self-gravity, the disk might become unstable to collapse and gravitationally-bound fragments will form. These fragments would then go on and develop to become planets.
Today’s astrobite focuses on this second route of gravitational disk fragmentation. Let’s take a brief diversion into a few parameters that help us analyze disk stability:
Disk Stability Parameters
One commonly used parameter when analyzing protoplanetary disk stability is the Toomre Q-parameter. This is given by 
is the sound speed in the disk (For astrophysical gases, the sound speed
where P and
are the pressure and density of the gas, respectively)
is the epicyclic frequency (this is roughly equal to the Keplerian frequency in protoplanetary disks. The Keplerian frequency
is the frequency at which an object at a given radius from the central star would orbit– for example the Keplerian frequency of our solar system at 1 A.U. is 1 orbit per year, since the Earth is at 1 A.U. from the Sun)
- G is the gravitational constant
is the 2-D surface density of the disk
Toomre showed in his seminal 1964 paper that for an infinitesimally thin disk to fragment, this dimensionless Q parameter must be less than about 1. Real disks are obviously not infinitesimally thin, but there is strong evidence that they can be quite thin (the thickness of the disk being sometimes of order 1/100 the radius of the disk), which gives us confidence in the Toomre analysis.
Another important scale is our old friend, the Jeans mass (or equivalently, the Jeans length), which we have talked about in previous astrobites. This is the scale at which gravity overcomes thermal pressure in a gas cloud. There are other parameters which are often used, such as the critical cooling time 
It is interesting to note here that many of the parameters and techniques used to study protoplanetary disks are also used to study accretion disks around compact objects, as well as the stability of disk galaxies!
Discussion of the paper’s Results
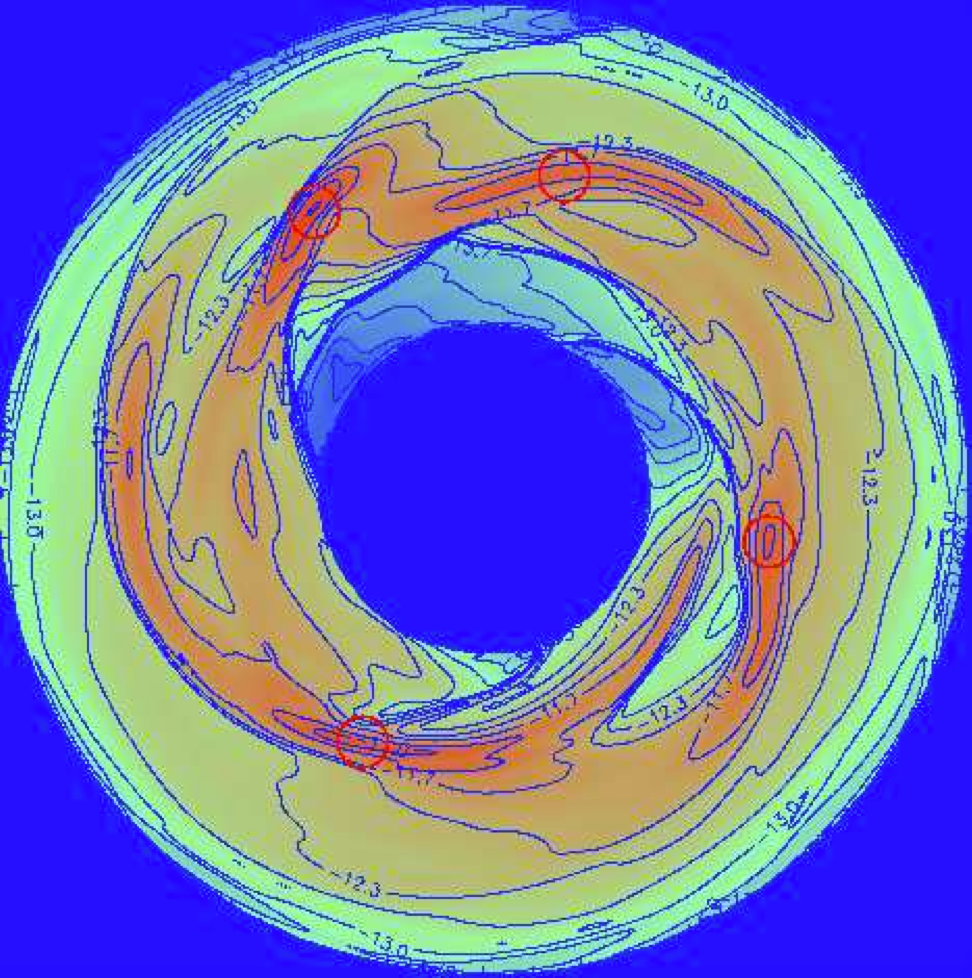
From Fig 5. of the paper. This plot shows the density contours of disk around a 1-solar-mass star after 547 years. Notice the strong spiral structure that is forming, within which the high density leads to gravitational fragmentation.
As in many astrophysical situations, the non-linear interplay between gravity and gas dynamics makes numerical simulations a crucial tool. In today’s paper, Boss carries out numerical grid-based simulations to determine whether gravitational instability can explain planet formation at orbital distances of about 30-70 A.U. (please see figure) It has been argued in past literature that core-accretion cannot explain planet formation at these distances, yet observations of such exoplanetary systems as the directly imaged HR 8799 indicate that large planets can exist at these radii. Note that these kinds of planets could exist in further-away systems as well. However most of these systems are far enough that they cannot be directly imaged, and the planets–if they exist– are far enough from their star that it is extremely difficult to detect them at current sensitivity with the traditional exoplanet transit/star-wobble methods.
The simulations generate clumps that, due to the fixed grid, cannot continue to become more dense like a real fragment would. But Boss argues that, since clumps keep spontaneously forming, the disk can be understood as fragmenting, even if each individual clump cannot be well-resolved for very long.
Boss finds that disk instability is indeed capable of forming giant planets on these relatively wide orbits. Furthermore, he finds that the number of protoplanets that are formed in the disk increases as the mass of central star and surrounding disk are increased. Boss concludes that HR 8799 is likely not an oddball system, and that future observations are likely to find more giant planets on wide orbits in other planetary systems.
Trackbacks/Pingbacks