- Three-dimensional Hydrodynamic Core-Collapse Supernova Simulations for a 11.2 M⊙ Star with Spectral Neutrino Transport
- Tomoya Takiwaki, Kei Kotake, Yudai Suwa
- First author’s institution: Center for Computational Astrophysics, National Astronomical Observatory of Japan
Core-collapse supernovae are some of the most energetic explosions in the universe and astronomers have devoted an incredible amount of both brain power and computational power to unraveling this astrophysical phenomenon. Despite this fact, the problem is far from solved.
The ‘standard model’ for these explosions begins when a star with an initial mass greater than ~8 solar masses has progressed through a series of nuclear fusion processes in its core, culminating in the burning of silicon into iron-56. At this stage, fusion can proceed no further and the outward pressure supplied by the energy produced during nuclear burning ceases. If the overlying star is massive enough, the core will be unable to support itself and begins to collapse. In this high energy environment photodisintegration (effectively the reverse of nuclear fusion) and electron capture convert the iron core into free neutrons. When the core reaches approximately nuclear density, pressure exerted by the strong nuclear force and neutron degeneracy cause the collapse to halt. The remaining infalling matter then “bounces” off the proto-neutron star, causing an outward propagating shock wave.
Ok, now hang with me. This is where it starts to get complicated… Simulations indicate that this initial shock is NOT what causes the supernova explosions we observe. Rather, additional photodisintegration and neutrino release cause the wave to lose energy and halt after less than a second. This produces a “standing shock” approximately 150 km from the proto-neutron star. In order for the system to explode, additional energy must somehow be pumped into the shock, causing further expansion. One of the current leading theories is that the proto-neutron star releases a portion of its binding energy as neutrinos, some of which are absorbed by the intervening material. This absorption process then drives convection, which acts to transport energy to the shock itself. This all seems well and good, but there is a slight problem: the initial set of simulations based on this physics consistently failed to actually explode the star.
I am now going to digress for a moment to discuss an important characteristic of many computational models: dimensionality. Despite the fact that we live in an age of supercomputers, computing time and power are still very much at a premium. Simulations of complex astronomical systems can easily take days, or even months, to run. One way theoreticians often reduce the amount of computing power required is by taking advantage natural symmetries present in the problem to reduce their system of equations from 3D down to 2D or 1D. For instance, the initial models of core-collapse supernova (the ones which failed to explode) assumed spherical symmetry. By doing so, they were able to simply solve the equations of radiative hydrodynamics along a radial axis. At first glance this seems like a reasonable assumption (after all, stars are roughly spherical), but a wealth of new observational evidence, such as the asymmetric shape of many supernova remnants or the connection between certain core-collapse supernova and gamma-ray bursts, indicate that asymmetry may, in fact, play an important role.
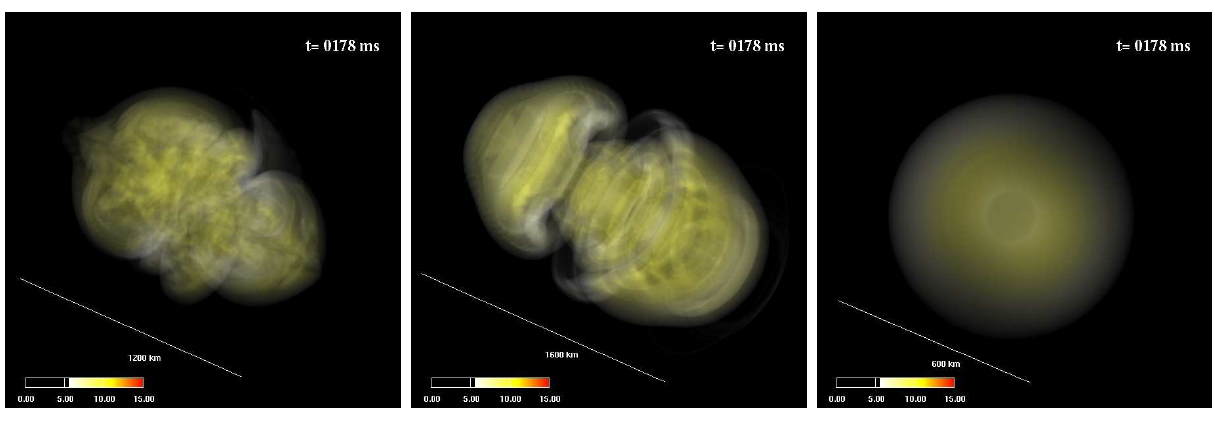
Volume rendering of entropy (energy) of the explosion for the 3D (left), 2D (middle), and 1D (right) simulation.
Indeed, when the models were expanded into 2D it was discovered that random perturbations caused acoustic modes (much like you would find inside an organ pipe) to form within the standing shock. This, in turn, caused a non-symmetric instability, the Standing-Accretion-Shock-Instability (SASI), to form and the shock wave was re-accelerated, causing the star to explode. The explosions produced by these models tend to be very weak, however, falling several orders of magnitude short of the 10^51 ergs observed in most supernovae. It is unclear at this point whether additional means of energy transport are required or if the sub-luminous explosions are simply an artifact of limiting the simulation to 2D (note that this imposes a preferred axis of symmetry which doesn’t exist in the physical system).
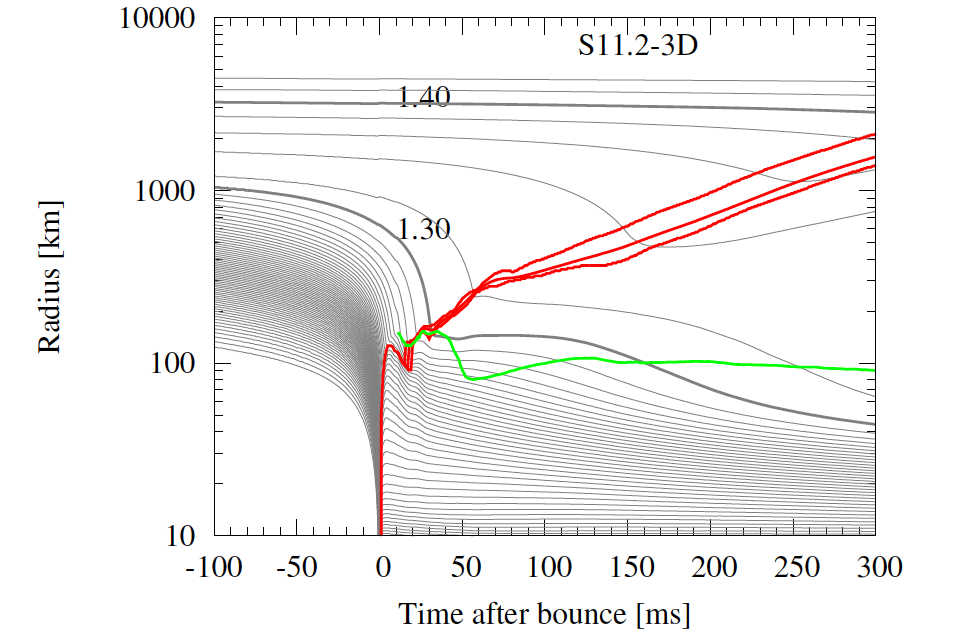
Time evolution of the shock wave. The red lines indicate the location of the shock wave for the 3D model. For comparison, the green line represents a 1D model, which does not explode.
It is this question that the current paper attempts to answer. The authors carry out both 2D and 3D simulations of the explosion of an 11.2 solar mass star with the same code (which models the supernova assuming reheating is triggered by neutrinos), and compare the results. They discover the following differences:
(1) The same acoustic modes dominate in both the 2D and 3D models.
(2) The convection driven is more vigorous in the 3D model.
(3) Non-axisymmetric motions cause particles to take longer to fall onto the proto-neutron star in the 3D model. This implies the particles are exposed to neutrino heating for longer.
(4) The neutrino luminosity is larger in the 3D model.
(5) The neutrino energy is smaller in the 3D model.
However, despite showing that quantitative differences between the 2D and 3D models exist, the authors caution that higher resolution simulations (i.e. more computing power) are necessary to assess whether any additional physics is necessary to reproduce the explosions we observe.



I’ve discovered a similar problem modeling magnetised shocks. Some of the features seen in 3d sims are not at all present in the 2d however, the amount of memory required to run the 3d sims makes them pretty unfeasible to study them well at this point. Thanks for the well written article!