• Title: Buoyant Magnetic Loops in a Global Dynamo Simulation of a Young Sun
• Authors: Nicholas J. Nelson, Benjamin P. Brown, Allan Sacha Brun, Mark S. Miesch, Juri Toomre
• First Author’s Institution: JILA and Dept. Astrophysical & Planetary Sciences, University of Colorado Boulder
Introduction
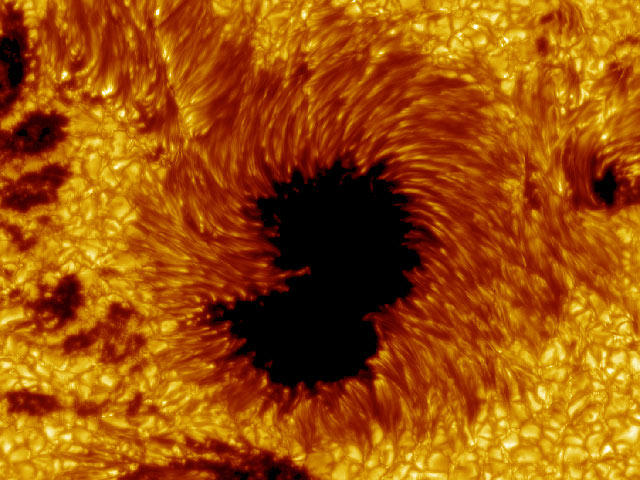
What is our current understanding of how sunspots are formed? We think that toroidal magnetic structures that exist deep in the Sun’s interior can become buoyantly unstable. As these magnetic loops become less dense than their surroundings, the buoyant force on them causes them to rise through the Sun’s interior. When they reach the photosphere, we observe the resulting flow of gas around them as sunspots.
These magnetic structures are ultimately due to dynamo action within the Sun: convection leads to differential rotation, which in turn amplifies toroidal magnetic fluxes that can buoyantly destabilize and rise. But this mechanism is not fully understood — and for this reason, solar researches have long sought to model the convective zone of the Sun. Their goal is to track the evolution of magnetic structures and, hopefully, reproduce the magnetic field configurations that we observe when sunspots occur.
That said, modeling the Sun is extremely difficult: activity within stars occurs over a huge range of length scales. In order to resolve everything in a 3D numerical simulation of magnetism, from the deep solar interior through to the upper atmosphere, we would need much greater computing power than currently exists. Three tricks that help us to tackle solar modeling are:
- Focus on one specific layer of the Sun at a time. In this case, the relevant layer is the convective zone.
- Model a star with a rotation rate that is greater than that of the Sun. This speeds up the process without losing any of the important physics, and since the Sun rotated at a greater rate when it was younger anyway, it’s not an unreasonable adjustment.
- Introduce diffusion, which smooths out motions on small length scales. This is a very important assumption for making modeling possible, since not needing to resolve the small scales significantly cuts back required computational time.
This last trick, however, can have some undesired physical effects. Previous studies examining magnetohydrodynamic (MHD) behavior in the Sun have run global convective MHD models that span the convective region. These studies have captured the formation of magnetic structures and cycles, differential rotation, dynamo action, and large-scale magnetic fields — but they’ve never captured buoyant magnetic loops which rise through the convective zone. The reason for this is precisely the diffusion introduced to make the simulation feasible: the buoyant loops diffuse before they’re able to rise to the surface.
Setup
In this simulation, the authors employ some clever mathematical modeling to mimic the effects of the unresolved small-scale features, reducing the magnetic diffusion by a significant factor without prohibitively increasing computational time. They model a region which spans most of the convective zone (from 0.72 R☉ to 0.97 R☉), and they use a rotation rate of 3 Ω☉.
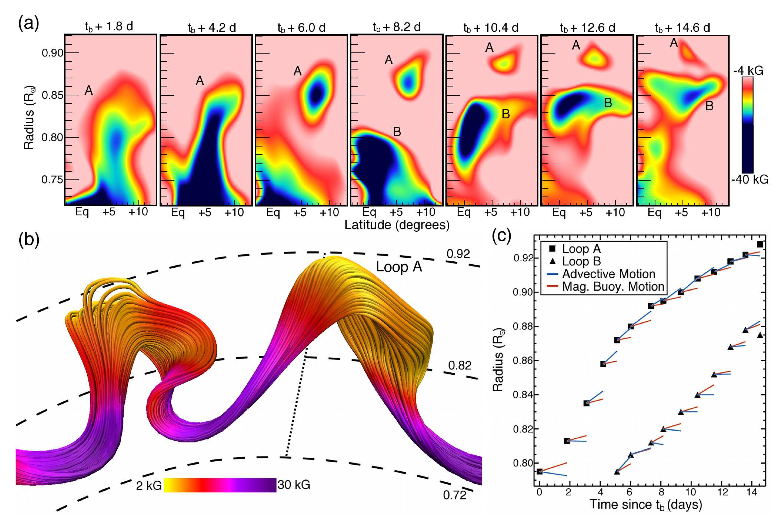
Figure 2: (click to enlarge) Analyzing a rising loop. (a) 2-D cuts in longitude at successive times. The rising magnetic loop A is seen in cross-section. Proto-loop B is also seen rising starting at 8.6 days, but the top of loop B never rises above 0.88R☉. (b) 3-D visualization of magnetic field lines in the core of a wreath which produces four loops (two shown here, one of which is loop A) at tb + 14.6 days. (c) Radial location of loop A and proto-loop B as a function of time. Fig 3 in the paper.
Results
As a result of this approach, the authors achieve the first 3D global MHD simulation that not only exhibits differential rotation, dynamo action, and global-scale magnetic structures — but also buoyant magnetic loops. In this simulation, the buoyant loops are generated by a convection/stratification/rotation-driven dynamo and rise as coherent structures to the top of the convective zone.
An example of their data is shown in Figure 2. The authors demonstrate that not all proto-loops successfully become buoyant and rise all the way to the surface (in the figure loop A reaches the surface, but proto-loop B does not); a threshold magnetic field must be exceeded in the region of the loop, and the loop has to interact favorably with convective flows to reach the surface. In Figure 2, proto-loop B encountered a convective downflow at 0.88 R☉ which interrupted its upwards motion and pushed it back down into the solar interior.
Conclusion
The authors warn that caution must be used in interpreting the results at the solar surface. Their work only extends to 0.97 R☉ due to the smaller-scale convection that happens at surface (granulation and supergranulation), which their simulation isn’t able to resolve.
Even so, extrapolating the loop’s expansion over the remainder of the trip to the solar surface, the authors obtain a loop size which is roughly that of a large sunspot. This suggests that this simulation depicts field configuration consistent with observed phenomena, and indicates that this work represents a significant step forward in numerical modeling of solar magnetic fields.