• Title: Shocking Results Without Shocks: Subsonic Turbulence in Smoothed Particle Hydrodynamics and Moving-Mesh Simulations
• Authors: Andreas Bauer, Volker Springel
• First Author’s Institutions: Heidelberg Institute for Theoretical Studies
Smoothed Particle Hydrodynamics (SPH) is one of the most commonly used techniques for simulating astrophysical fluids. Previous astrobites have discussed the the theoretical basis for SPH, how to set up and run an SPH simulation using the Gadget-2 code, and some recent research results based on SPH calculations, so I won’t go into too much background detail here. Briefly, an SPH code uses particles to represent a fluid. By applying a sampling kernel, the code can estimate the gas density at any position based on the locations of nearby particles in 3D space, and using that estimate, predict particle accelerations due to gas pressure forces and self-gravity. SPH is very straightforward, versatile, and robust. Unfortunately, as pointed out by this paper and several other recent studies, SPH has serious shortcomings.
This particular paper focuses on a regime of gas dynamics that is often neglected in astronomy: subsonic turbulence. Just as the air in the upper atmosphere exhibits random motions that can buffet an airplane cabin, the gas in interstellar space also exhibits random, turbulent motions. In the atmosphere, the turbulence is subsonic, i.e. the typical velocity of the air is much less than the speed of sound. In this regime, the density of the gas does not change much, since pressure forces have time to move the fluid out of the way if an overdensity develops. On the other hand, when a fluid is supersonically turbulent, generally it is characterized by volume-filling networks of shock waves marked by overdense filaments. While subsonic turbulence occurs quite often in our everyday experience, supersonic turbulence is ubiquitous in interstellar space. For this reason, most studies of astrophysical turbulence have focused on the supersonic regime. SPH has historically compared very well to other methods when simulating supersonic turbulence. It’s therefore not so surprising that no one has tested the capabilities of SPH in the subsonic regime, since only astronomers tend to use SPH codes.

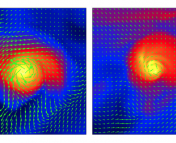
A comparison of a subsonically turbulent fluid simulated in Arepo code using a moving mesh (left), in fixed-grid mode (center), and the SPH code Gadget-3 (right). SPH does not resolve small-scale motions that are well-resolved by AREPO.
Unfortunately, SPH fares very poorly in the subsonic regime. Above, I’ve reproduced a comparison of gas velocities, densities, and enstrophies (a measure of the swirlyness of the motion of the fluid) for a driven subsonic turbulence test problem in a fixed grid code, a moving mesh code, and an SPH code. In all three cases the fluid is stirred up in precisely the same way. Ideally, all three codes would produce the exact same answer. While the grid codes do agree to a high degree of precision, the SPH code seems to be quite different. While the grid codes exhibit rich structure at large and small spatial scales, the SPH code seems to not have any power at small scales and is quite noisy, particularly in the enstrophy map.

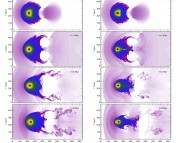
The power spectra, kE(k), for subsonic turbulence when simulated by AREPO in moving mesh mode (A3), fixed mesh mode (F3), and when simulated by the Gadget-3 SPH code (S3). The dotted line marks where the codes are nyquist sampled, indicating where both codes must break down due to finite resolution.
Subsonic turbulence is advantageous to study in that there is a relatively simple analytic theory by Kolmogorov that describes the properties of a subsonically turbulent fluid. An important prediction of Kolmogorov theory is that energy is deposited into the fluid at large scales, driving motions in the fluid, which in turn drive motions at increasingly smaller scales, until eventually the kinetic energy in the fluid motion is damped by viscosity and converted into heat at molecular scales. This information is encoded in the power spectrum, E(k), the energy at a given wavenumber, k = 2π/λ. A specific prediction of Kolmogorov theory is that E(k) should be proportional to k-5/3. The analytic prediction is plotted at right, along with the measured power spectra for the grid codes and for SPH. The intuitive conclusion one draws by inspecting the images of the simulations are confirmed boldly: SPH does a terrible job of resolving small-scale motions and predicts a power spectrum that is far too steep. The grid codes do better, although predict an excess of power at small scales due to the bottleneck effect. This is a damning result. One should only use SPH to model subsonic turbulence with extreme caution and skepticism.


For an opposing view, see: http://arxiv.org/abs/1111.1255v1
Hey Nathan,
For the supersonic regime, is SPH always a feasible method? If not what kind of situations would make it fail? I’m interested in knowing some criterion for when to use a mesh based method or Spectral or SPH. Thanks.
Hi Brian,
I suggest you read Price and Federrath (2010). The short answer is that it really depends on what you’re interested in. You also have to be careful that you fully understand the properties of your simulation.