- Title: Measuring NIR Atmospheric Extinction Using a Global Positioning System Receiver
- First Author: Cullen H. Blake et al.
- First Author Institution: Princeton University Department of Astrophysical Sciences
Attenuation of light by the Earth’s atmosphere is one of the biggest challenges facing observational astronomers. Line absorption, Rayleigh scattering, and aerosol scattering can all affect observations in the optical and infrared. Water vapor in particular has many absorption features between 900 and 2500 nm, and often has large and rapid variations in optical depth. This paper presents a method to derive the Precipitable Water Vapor (PWV) using a Gobal Positioning System (GPS) device at the observing site. Using these GPS estimates, the authors calculate theoretical transmission spectra that are an excellent fit to real spectra in the range of 900 to 1000 nm.
Measuring PWV
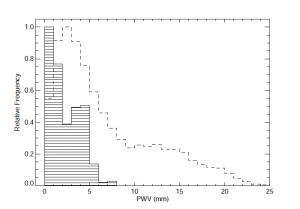
Precipitable Water Vapor is the height that a column of water vapor would take if condensed, and is proportional to the optical depth due to absorption by water. Optical depth in turn determines how much incoming light is absorbed. Although normally measured with balloon-borne radiosondes or mid-IR radiometers, GPS systems can also measure PWV: their microwave signals are delayed by both the ionosphere and the neutral atmosphere, so by measuring the total delay and the ionospheric delay, we can estimate the delay due to water vapor. The ionospheric delay component is calculated using two different signal frequencies. The total delay (TD) of the dry atmosphere component is made up of the Zenith Hydrostatic Delay (ZHD), due to dry air, and the Zenith Wet Delay (ZWD), due to water vapor. A barometer accurately calibrates the ZHD, and the difference ZWD = TD – ZHD, proportional to the water vapor, is easily found. The authors determine a linear relation between the optical depth and the calculated PWV measured in millimeters. In the figure below, we see a histogram of PWV measurements at Apache Point Observatory (APO), located in the Sacramento Mountains of New Mexico. Although most of the time the PWV is quite low, the absorption due to water can occasionally increase quite dramatically on short timescales — and this effect is what the paper aims to correct.
Creating an Atmospheric Model
In order to model atmospheric absorption, the authors created theoretical transmission spectra that take into account the optical depths of all the components of the Earth’s atmosphere. Specifically, they used previously-calculated line widths, strengths, and centers for water transitions from 600 to 11000 nm for 80 km of atmosphere. The majority of atmospheric components are taken from the NASA-MSFC Earth Global Reference Atmospheric Model, but the highly time-variable water vapor components are taken from their GPS measurements.
Fitting to A Stars
To test the transmission spectra, the authors observed 74 standard A stars using the ARCES spectrograph on the 3.5 m telescope at APO. They focused on the range of 970 to 986 nm, in which A stars lack spectral features and water has numerous lines. The atmospheric model, which is a function of the calculated PWV at the time of observation, is convolved with the ARCES line spread function and normalized by a stellar continuum function to obtain the final model spectrum. The model spectra are a very good fit to the actual data, as seen in the next figure.
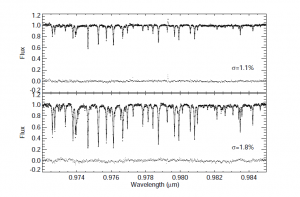
Two fits to A star spectra. Observations are points and solid lines are theoretical spectra. The absorption lines due to water in the atmosphere are well-predicted by the GPS-measured PWV.
Extensions to SDSS
The Sloan Digital Sky Survey (SDSS), also located at APO, includes photometry of over 260 million stars in five bands. The SDSS z band is a red filter centered at 913 nm, and is the closest to the wavelength range considered in the paper. Although the data have already been calibrated for atmospheric extinction, the authors believe that the complexity and timescale of atmospheric components in the z band will lead to large residuals for objects with complex spectral energy distributions, such as M Dwarfs. By using the leverage of GPS water vapor measurements at the specific observation times, it should be possible to better calibrate photometry in this region, where water absorption is important.
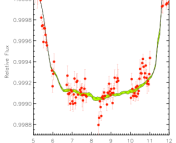
The authors first selected 7300 M Dwarfs and estimated the PWV at the time of each observation. Since there was no GPS-based PWV monitor at APO during SDSS’s observing run, a similar monitor at White Sands, 50 km away, was used instead. Measuring the correlation of water vapor between White Sands and APO shows that they are highly correlated. The authors are thus justified in using White Sands PWV measurements taken during the SDSS run as a proxy for water vapor at APO. The authors plotted the M Dwarfs and measured the difference between the measured colors of the stars and the stellar locus, and found that they could correct for the color difference as a linear function of the PPV at the time of observation.
Next, a sample of 3000 G and F stars and 2500 M stars was taken. The average z-band magnitude over time was calculated for each object, and compared to the average magnitude only for those times when the PPV was less than 4 mm. For G and F stars, the effect of water vapor was small, but for M stars the authors obtained a magnitude correction that is consistent with that of the first sample. This result confirms the authors’ hypothesis that the complexity of objects in the z band makes their photometry more difficult, and that the effect can be mitigated using the GPS method.
Conclusions: Why does this matter?
Using contemporaneous GPS-based PWV measurements can help to correct for many of the effects of water absorption in red and near infrared wavelengths, leading to higher precision in photometric measurements. Specifically, it can take into account the relatively large effect of water vapor changes on short timescales, which is lacking in many observing facilities. This method can also be used to historically correct for PWV changes if a GPS receiver was present during the observation. This improvement in precision is important for several current astrophysical problems, including that of finding transiting planets around M stars. GPS measurements of PWV may be used as a part of the calibration strategy for large surveys such as LSST, or as a strategy for characterizing an instrument’s spectral response.
Also, be sure to check out these two (unrelated) links!
1. Chembite on Mars surface chemistry:
http://chembites.wordpress.
2. Bob Kirshner’s op-ed in the NYT on the Nobel Prize:
http://www.nytimes.com/2011/



Hi Kirit, nice review.
Astrobites readers may be interested in NOAA’s GPS Meteorology network accessible through this website:
http://gpsmet.noaa.gov/test/cgi-bin/gnuplots/rti.cgi
Which provides near real time IPW measurements along with temperature and pressure for many locations across the US. Some observatories have partnered with NOAA and have such a system installed nearby.
Thanks for the link, Brian. This looks very useful!