- Title: Missing black holes unveil the supernova explosion mechanism
- Authors: Krzysztof Belczynski, Grzegorz Wiktorowicz, Chris L. Fryer, Daniel E. Holz and Vassiliki Kalogera
- First Author’s Institution: Astronomical Observatory, Warsaw University, Poland
Today’s Astrobite was contributed by Warrick Ball, a graduate student at the Institute of Astronomy at Cambridge. If you would like to contribute to Astrobites, please contact us!
Though we’re still trying to understand why, it’s quite clear that stars are born with masses drawn from a fairly continuous distribution, the initial mass function. When they die, many leave compact remnants: white dwarfs, neutron stars or black holes. You might think that stars with an approximately continuous distribution of masses would lead to remnants with an approximately continuous distribution masses. But you’d be wrong.
It turns out that there’s a “mass gap” between the heaviest neutron stars and the lightest black holes. The former weigh in at about 2 M☉; the latter about 5 M☉. It’s possible that the gap appears because of something about the way we look at black holes but if the gap is real then there must be something about the way these remnants are created. This is what the authors of today’s paper try to work out. What does the mass gap tell us about the way supernovae form compact remnants?
First, let me review core-collapse supernovae. These supernovae occur when the iron core of a massive star (more than 8ish M☉) becomes unable to support itself against gravity and starts to collapse. Everything falls inwards until the core reaches densities like that of an atomic nucleus. Suddenly, the core becomes so stiff that the material falling onto it bounces right off. A shockwave travels through what was the stellar envelope, pushing it back out.
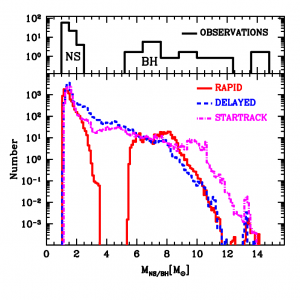
Figure 1: The number distribution of black hole and neutron star masses from observations (top) and the authors' models. "STARTRACK" is a typical population synthesis code, which might need to be reconsidered. Note that only the "rapid" model reproduces the gap seen in the observations.
It turns out the bounce isn’t enough to remove the envelope. It stalls as it travels outwards. Something else has to give some extra juice to restore the stalling shock. The gravitational potential of the collapsing core implies that there are hundreds of supernovae-worth of energy available but it isn’t clear how it couples to the envelope to cause an explosion. A good option is that the gas absorbs some fraction of the neutrinos released when core turns its protons into neutrons. (These neutrinos were detected when supernova SN1987A happened and are being cited as evidence against neutrinos being able to travel faster than light.)
The authors consider two options for how this energy is captured. In their “rapid” model, neutrinos heat and rarefy the material just outside the core. This means hot, sparse material sits underneath cold, denser gas so Rayleigh-Taylor instabilities kick in, causing convection to begin. Broadly speaking, convection means blobs of gas near the core heat up, become buoyant, float upwards and disperse heat into their surroundings. Blobs of cold gas near the shock do the opposite and the net result is outward energy transport. It’s a bit like a lava lamp, albeit an incredibly hot and violently turbulent lava lamp. Simulations suggest it takes less than a few hundred milliseconds to get enough heat out to drive an explosion. Any slower and the mechanism fizzles out, leaving the envelope to fall back onto the collapsing core.
The second model the authors consider is the “delayed” model. In this case, the original bounce pushes an outward shock which is struck by the material that is still falling inwards. The impact of the free-falling gas kicks up a range of instabilities that send pressure waves through the hot gas around the core. When these waves interact, they impart energy into the turbulent plasma that can drive the explosion. This process is probably much slower than the rapid model. Strong instabilities have been found to take more than half a second to develop.
The final piece of the theoretical puzzle is the density of the layers around the core. Beyond the innermost iron there are layers of everything that was burned to get there. Most important are the silicon and oxygen layers. The authors liken the moments before the supernova to a pressure cooker: the heat in the pot depends on the models described above and the weight of the lid depends on the layers of material around the core. The weight of these layers depends on whether the core was convective when those elements were made. These burning phases are convective for stars more massive than about 20 M☉, so they have heavier “lids” than you’d expect by extrapolating from smaller stars.
I’ll try to summarize. The iron core collapses and the envelope bounces off once it reaches nuclear densities. The bounce needs a boost, which it gets either from Rayleigh-Taylor instabilities around the core (“rapid”) or from pressure waves initiated by a standing shock (“delayed”). The explosion then depends on whether enough energy is deposited under the stalled shock to blast off the weight of the silicon and oxygen layers, which in turn depend on whether they were created in a convective core. So what do the authors find?
In short, everything points towards the rapid model. For stars between 8 M☉ and 14 M☉, the neutrinos alone seem to be enough to heat the gas and give the cooker enough pressure. Up to 20 M☉, the lid can hold the gas in a bit longer so, in the rapid model, convection starts up and adds to the pressure in the pot until the supernova happens, leaving neutron stars up to about 2 M☉. Beyond 20 M☉, the rapid model can’t get enough energy into the gas to stop it pretty much all falling back under the weighty outer layers. The jump from nearly no fallback to nearly complete fallback makes the mass gap. Remnants are black holes of at least 5 M☉. In the delayed model, the extra time allows more fallback in stars just lighter than 20 M☉ and weaker shock instabilities in stars that are just heavier. These collude to smear the black hole mass range across the gap.
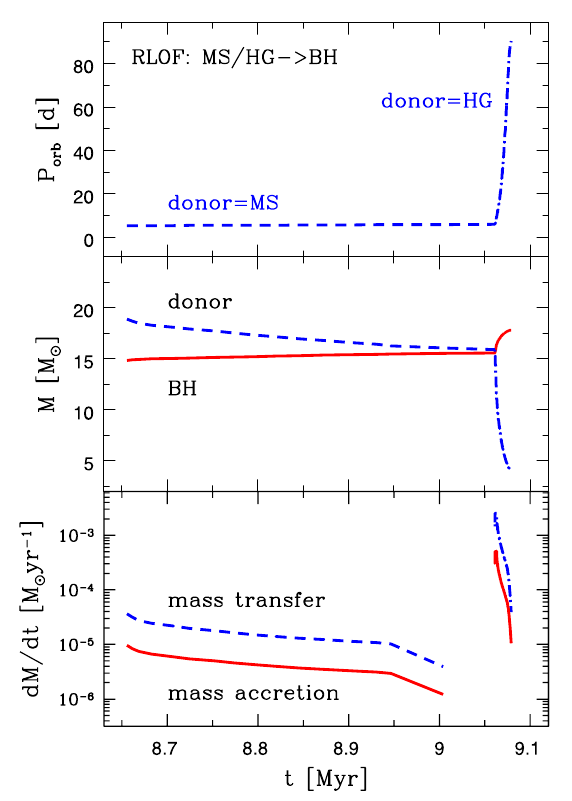
The authors finish off by considering how much their result could be affected by accretion of material in a binary system. The short answer is “hardly”. In low-mass x-ray binaries, the donor star isn’t big enough to make a dent in the distribution. For high-mass x-ray binaries, the mass ratio between the black hole and donor is so big that most of the accreted gas is probably ejected from the system, so the growth of the black hole remains small. Although there probably are 3 M☉ black holes out there, our current observations show that there must be very few. The authors of today’s paper have used this experimental fact to constrain the very complicated theory about how they form in supernovas. And constraining theory with evidence is what science is all about.