- Title: Was the Sun Born in a Massive Cluster?
- Authors: Donald Dukes and Mark R. Krumholz
- First Author’s Institution: University of California, Santa Cruz
It is observational and theoretical consensus that most stars form in clusters. A cool, dense cloud collapses via gravitational instability and then fragments into individual protostars. The majority of the gas in the cloud is not converted into stars, and this gas is blown out of the cluster by the strong winds of massive young stars. Without this gas, the cluster becomes unbound and the stars in it disperse.
Aside from its role as the source of all known life in the universe, our Sun is quite unremarkable. Two lines of observational evidence suggest that the Sun formed in a cluster like most stars. First, evidence of short-lived radio-isotopes in meteorites strongly suggest the presence of at least one polluting supernova (M > 25 solar masses) in the vicinity of the solar nebula. A lower limit on the natal cluster size of 1000 stars can be estimated by finding a cluster mass that will form at least one 25 solar mass star. However, the lifetime of a 25 solar mass star is much longer than the lifetime of a cluster. The cluster lifetime requires a shorter-lived star so that the solar nebula may be polluted by the time the cluster disperses, placing a modified lower limit of 75 solar mass on the supernova progenitor mass. A new lower limit on the total cluster size of 10,000 stars is thus invoked so that at least one 75solar mass star is produced from a Salpeter IMF.
On the other hand, we observe a Solar System with 8 planets in circular orbit and a mildly truncated Kuiper Belt of small-sized primordial objects. Previous simulations that imposed the constraint of low-eccentricity planetary orbits find that this places a strong upper limit on the cluster size of 2000 stars. According to the old paradigm, increased cluster size yields an increased number of dynamical interactions and therefore decreased likelihood that the solar system would remain unperturbed today. There is one massive Kuiper Belt Object object with high eccentricity, Sedna, so a good model of cluster mass would ideally perturb the orbit of a few percent of Kuiper Belt Objects while leaving the Jovian planets unperturbed.
A theoretical picture of the solar system’s natal cluster must be able to explain the seemingly conflicting geochemical and dynamical constraints that the observations impose. This paper provides new insight into the problem by modeling the probability of solar system disruption as a function of natal cluster mass and surface density and including updated observations of cluster lifetimes. The previous studies of solar system stability used a cluster lifetime of 100 dynamical times, producing a solar system that is highly subject to collision over the course of the time it spends in its natal cluster. More recent studies show that a more appropriate cluster lifetime is 1-4 dynamical times.
This study examines the probability that a Jovian planet will experience a disruptive event during its stay in the natal cluster. They first determine the impact parameter for such an event for each Jovian planet as a function of incoming stellar velocity (Fig. 1). Notice that the impact parameter decreases with collision velocity.
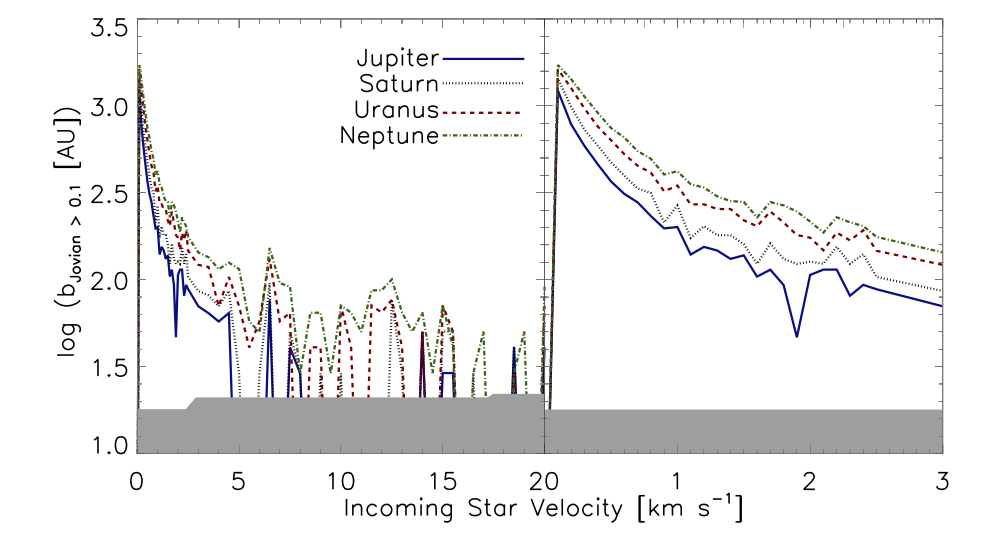
Given the velocity dependent impact parameter, they simulate 2.1 million collisions of our solar system with other cluster stars. Included in our solar system is the sun, the four Jovian planets, 350 Kuiper Belt Objects, and Tyche. The collision parameters are sampled from a Chabrier distribution of stellar masses, a Maxwellian distribution of collision velocities, and randomized impact directions. They assign stellar companions to the incoming star according to the mass dependent companion fraction, and the orientation of the binary system’s orbital plane with respect to the ecliptic is randomized. The probability that a planet is significantly perturbed is the number of perturbing collisions divided by the total number of collisions. The results of the simulation are shown below (Fig. 2). Note that the probability of a perturbing collision decreases with cluster mass. Although at first counter-intuitive, this is explained by realizing that cross section decreases with velocity dispersion and therefore cluster mass, while the number of collisions stays constant with cluster mass for a given surface density. As the probability of disruptive interaction scales with the number of collisions and cross section, the total probability decreases with increased cluster mass. The probability of perturbation is low for all values of cluster mass and surface density, placing no upper limit on cluster mass by this diagnostic. The probability of Kuiper Belt orbit disruption is also very low for all simulated cluster densities and masses.
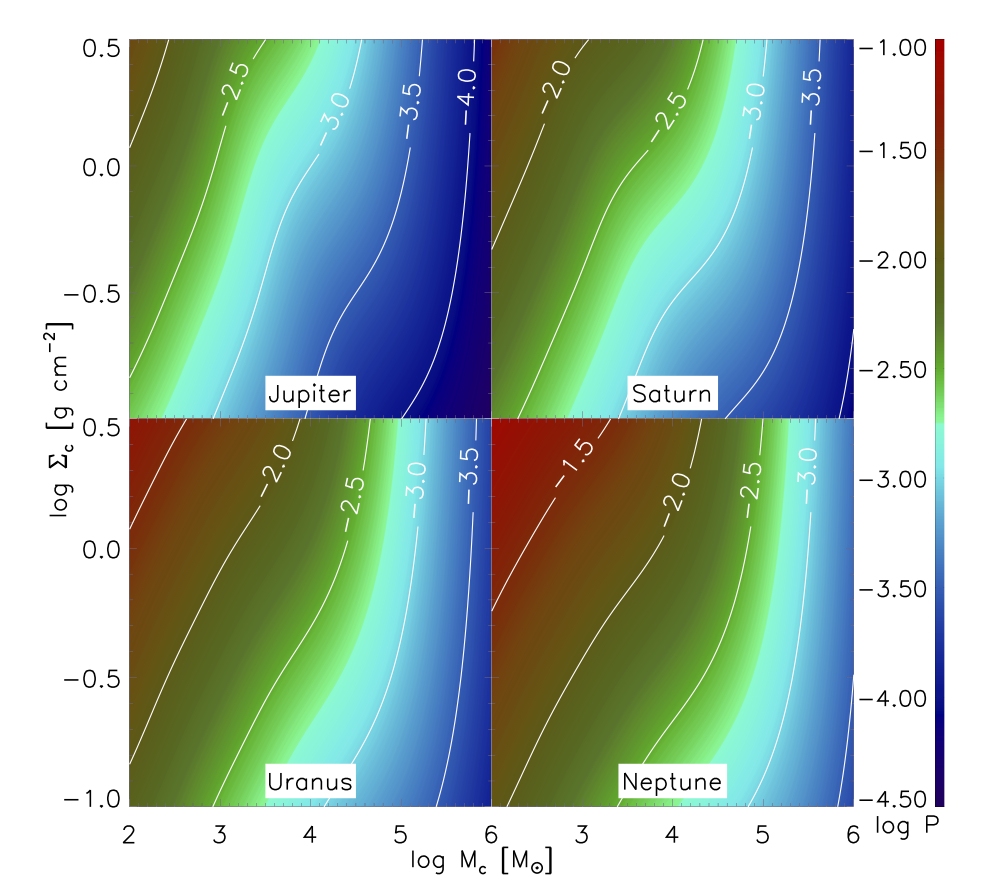
The take-home message: Improved estimates of cluster lifetimes lift the previously derived upper limit on the mass of the sun’s natal cluster, allowing for a reconciliation between the dynamical and geochemical constraints on the initial mass of the cluster.

Trackbacks/Pingbacks