Title: A catalogue of rotation and activity in early-M stars
Authors: Ansgar Reiners, Nandan Joshi, Bertrand Goldman
First Author’s Institution: Institute for Astrophysics, Göttingen
In December, I was sitting in the summer sun in Chile after an observing run, reading a paper about M dwarfs by Reid et al. (2002). I came across this choice quote: “Even if [M dwarfs] are now a shade passé . . . .” Since I had just spent three nights on a very large telescope observing M dwarfs, I found this highly amusing. Regular Astrobites readers will be aware that M dwarfs are decidedly not passé, having received a burst in popularity due to the relative ease of finding their orbiting Earth-sized planets. They are of course interesting in their own right – that quote finishes up: “analyses of enlarged samples can probe such fundamental parameters as the stellar mass function, Ψ(M), kinematics and the origin and range of magnetic activity close to the hydrogen-burning limit.”
Introduction
This paper delves into some of the physical properties of early M dwarfs (M0-M4.5), focusing on chromospheric/magnetic activity and rotation. Courtney presented a paper on a similar subject in a previous astrobite, although the work by McLean & others (2011) focuses on late M and L dwarfs, which are smaller, cooler and fully convective. As Courtney discusses, there is thought to be a change in the mechanism that produces a star’s magnetic field as it crosses the boundary from partially convective to fully convective.
Methods
To measure activity, Reiners & others use the emission of H-alpha photons, known to trace magnetic activity in the outer layers of M dwarfs. They measure the strength of the H-alpha emission, which is called the “equivalent width.” The equivalent width is essentially the amount of flux in excess of the background level within this emission line. If H-alpha emission is detected, a star is considered to be magnetically active.
The authors use rotational broadening to measure projected rotation velocity: due to the Doppler effect, the spectral features of a spinning star are broader than they are naturally.* The process used to determine projected rotation velocity (cross-correlation with a template spectrum) can also identify binary stars; the authors find 20 definite binaries and 13 other possible binaries.
Results
Reiners & others combine their high resolution spectra with results from the literature for a final sample of 334 M dwarfs, which includes 157 new measurements of projected rotation. This sample does not represent an unbiased sample. Earlier M dwarfs are brighter than later types and can therefore be seen out to farther distances (with their magnitude limits, 19pc for the earlier types versus 12pc for the later types); therefore, a disproportionate number of early stars are included.
The authors find that both magnetic activity and rotation have a strong dependence on spectral type, which can be seen in the two figures below: 5% of stars in the “early” subset of stars (M0-M2.5) are magnetically active, while 41% of the “mid” subset (M3-M4.5) are active, with rotation showing a very similar trend. The strong correlation seen between activity and rotation is expected, and means that later M dwarfs are capable of sustaining fast rotation periods and magnetic fields longer than earlier M dwarfs. The 5 rapidly rotating early stars are also among the 7 active ones; these can be explained by their young age or by virtue of being in a binary, which can preserve rapid rotation and activity beyond the expected lifetime. Finally, there does not seem to be a break in behavior as the stars cross the fully convective boundary, implying that the magnetic dynamo continues to be driven by rotation (even if the mechanism behind the dynamo changes).

The fraction of active M dwarfs in each spectral type bin, showing a strong increase as we move to later spectral types. There is also a strong correlation between activity and rotation. Figure 5 from the paper.
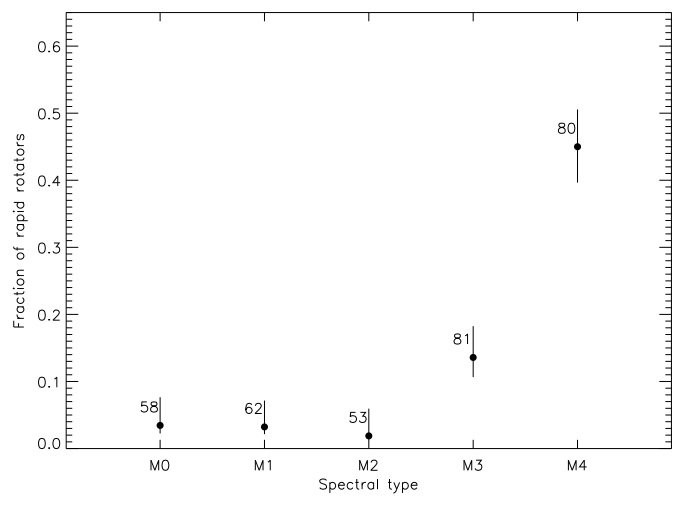
The fraction of rapidly rotating M dwarfs in each spectral type bin, showing a strong increase as we move to later spectral types. There is also a strong correlation between activity and rotation. Figure 8 from the paper.
* When a star is spinning, the light we receive from the receding side is redshifted and that from the approaching edge is blueshifted. The magnitude of these shifts (caused by the Doppler effect) depends on the velocity with which the outer layers of the star are rotating. However, only projected rotation, called v sini, can be measured. It’s called v sini because it is the true rotation velocity multiplied by the sine of the inclination: if viewing a star from the pole (i=0), you will measure v sini = 0 no matter how fast it’s rotating because no parts of the star are moving toward or away from you.


Trackbacks/Pingbacks