TITLE: Scaling relations for galaxy clusters in the Millennium-XXL simulation
AUTHORS: R. E. Angulo, V. Springel, S. D. M. White, A. Jenkins, C. M. Baugh, C. S. Frenk
FIRST AUTHOR’S INSTITUTION: Max-Planck-Institute for Astrophysics, Garching, Germany
In a perfect world, there would be one observable quantity (or even better, two or three) of galaxy clusters that would correlate simply and robustly with the total mass of the cluster. This would allow astronomers to easily determine the masses of potentially thousands of clusters. Then, armed with these precise masses, we could greatly advance our understanding of cosmology, since the distribution of cluster masses is sensitive to the fundamental parameters of the universe. Unfortunately, cluster scaling relations in reality have proven to be surprisingly complicated, and recent studies have found puzzling discrepancies between observed results and our expectations (check out this paper as one recent example).
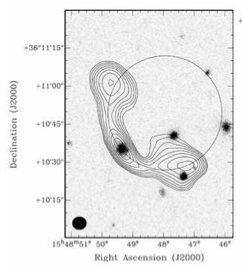
Figure 1: The four clusters with the largest tSZ signal, X-ray luminosity, weak lensing mass, and optical richness count. Note the differences in structure between these massive clusters. (Fig. 1 of Angulo et al.)
The authors of this analysis use the largest, high-resolution cosmological N-body simulation to date, the Millennium-XXL (MXXL), to investigate sources of scatter in cluster scaling relations. The MXXL follows the non-linear growth of 303 billion dark matter particles within a cubic region of 4.11 Gpc on a side. This simulated volume is equivalent to that of the observable universe out to a redshift of z = 0.72. The goal of the work is to ‘measure’ various cluster properties from the simulation while replicating the techniques of typical observational surveys. Then, the authors compute the relations between these observables and cluster mass to determine if the results match our theoretical expectations.
The four cluster observables that the authors examine are the ‘optical richness’ 
These observed properties of clusters depend not only on the dark matter in a halo, but also on the hot gas in the cluster, which the MXXL does not model. Instead, the authors construct simple proxies for each of the observables, based solely on the dark matter structure, which nicely avoids any uncertainties in modeling the interplay between the dark matter and gas.
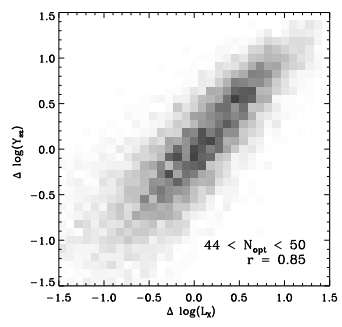
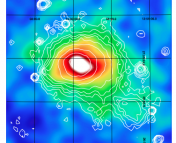
Figure 2: The correlation between deviations in the tSZ signal (y-axis) and X-ray luminosity (x-axis) of a cluster at fixed optical richness. (Fig. 7 of Angulo et al.)
Each of the four cluster observables has intrinsic selection effects, as illustrated by Figure 1. This figure shows the four clusters with the largest tSZ signal, X-ray luminosity, weak lensing mass, and optical richness count in the MXXL. The structure of these clusters varies immensely, and the cluster with the largest mass is, in fact, the one with the largest optical richness. The authors argue that selection effects such as these must be carefully considered before drawing cosmological conclusions from a sample of clusters.
First, the authors determine the intrinsic scatter between cluster observables and find that there is a positive correlation between the deviations in pairs of observables. This means that a cluster with a higher than average signal in one observable will likely have a larger signal for each of the three other measured observables as well. The largest correlation is found to be between the scatters in tSZ signal and X-ray luminosity, at fixed optical richness (see Figure 2). The authors argue that these correlations result from the fact that each observable is sensitive to the same set of properties of the cluster population, including internal structure, orientation and environment, and line-of-sight projection of matter not associated with the cluster.
Furthermore, the authors investigate the discrepancies introduced by the particular strategies of an observational survey. As an interesting case study, they address the recent inconsistencies between the mean tSZ signal for optically and X-ray selected clusters found by the Planck collaboration. The stacked mean tSZ signal for a set of clusters at fixed optical richness was found to be significantly lower for optically selected clusters than for X-ray selected clusters. But why?
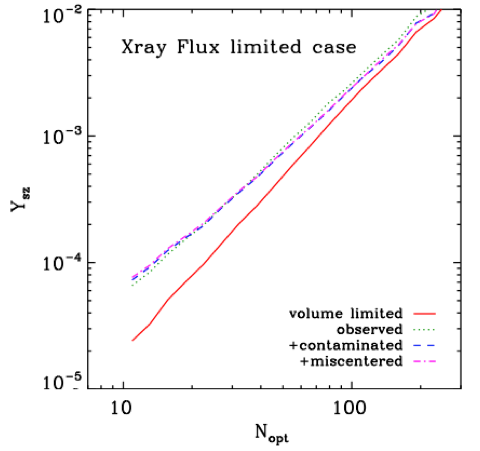
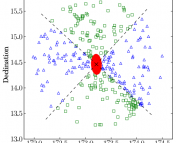
Figure 3: The mean tSZ signal as a function of optical richness for a X-ray flux limited sample from the MXXL. The result using a volume limited sample from the MXXL is shown in red, significantly below the X-ray flux limited results. (Fig. 9 of Angulo et al.)
The authors of this work argue that this discrepancy is likely the result of a phenomenon known as Malmquist bias. This effect causes some surveys to preferentially select intrinsically brighter objects. In the Planck team’s analysis, the optically selected catalog is roughly volume limited (i.e., they select all clusters within the survey volume), while the X-ray catalog is approximately flux limited (i.e., they select all clusters above a given X-ray luminosity). Thus, the X-ray selected catalog preferentially includes more clusters of higher than average X-ray luminosity. The authors then argue that the intrinsic correlation between the scatters in
The authors’ analysis of scaling relations for clusters in the MXXL indicates that a wide range of effects and biases must be properly considered before making cosmological inferences from a galaxy cluster survey. These biases depend both upon the inherent properties of the cluster population being considered and on the survey-specific techniques used to estimate each observable from the data. This work represents an important step forward in understanding how these biases affect the most commonly used cluster scaling relations in cosmology.
