Title: Sensitivity of Stacked Imaging Detectors to Hard X-ray Polarization
Authors: Fabio Muleri and Riccardo Campana
First Author’s Institution: Istituto Nazionale di Astrofisica, Rome, Italy
Several new experiments are in the works to observe the X-ray sky at energies greater than 10 keV, such as Astro-H and NuSTAR. While these and previous X-ray telescopes have provided imaging capabilities, only a few polarization measurements have been made in this energy band. Since polarization provides another important window into astrophysical phenomena, it would be very useful if X-ray imagers could also back out the radiation’s polarization state. In this paper, the authors perform simulations to determine the sensitivity of a generic multi-layer X-ray optical design to incident polarization.
Compton Scattering
The key to understanding X-ray polarization measurements is Compton scattering. In this process, high energy photons scatter inelastically off electrons in matter, losing kinetic energy (the more familiar Thomson scattering is just the low-energy limit of this effect). As a result of the collision, the photon’s energy changes as a function of the scattering angle (Figure 1).
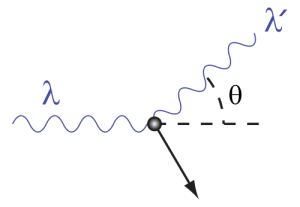
Figure 1: Compton Scattering Geometry. A photon is incident on an electron and scatters off. The photon's wavelength changes depending on the scattering angle.
A Stacked Imaging Polarimeter
Many broad-band X-ray imagers consist of two stacked detector planes, each dedicated to absorbing photons of different energies. The first is commonly made of Silicon which responds to photons in the 1-15 keV range, while the second is made of CdTe or CZT crystals absorbing in the 100 keV range (Figure 2).
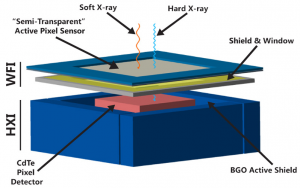
Figure 2: The Wide Field Imager on the proposed International X-ray Observatory. Notice the two layers absorbing X-rays of different energies.
These detectors are inherently sensitive to polarization. Though the vast majority of high energy photons pass through the first plane without interaction, the Silicon will absorb or scatter a small fraction. If a scattered photon is then absorbed by the second detection plane, the two detections can be correlated to find the direction of scattering. The polarization state of the incident photon can then be recovered using the scattering angle and photon energy.
Distinguishing Double Events
Correlating an absorption in the second plane to a scattering in the first can be a challenge. First, the scattering event must deposit energy above the Silicon detection threshold. Next, the timing must be right. The signals from the planes occur essentially at the same time, but one must be careful to minimize the probability of accidental coincidences due to background pileup. Finally, knowing the energy released in the first detector, one can determine the maximum scattering angle and thus draw a hollow cone in which a coincidence event can occur (Figure 3). If a photon absorbed in the second plane corresponds to a scattering in the first plane both in time and space, its polarization can be found.
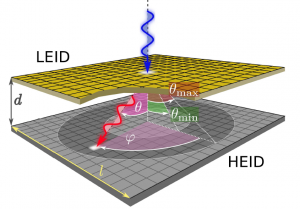
Figure 3: Geometry of Double Events. The photon scattering off the Low Energy Imaging Detector (LEID) can only be absorbed in a hollow cone projected on the High Energy Imaging Detector (HEID).
Simulation Results
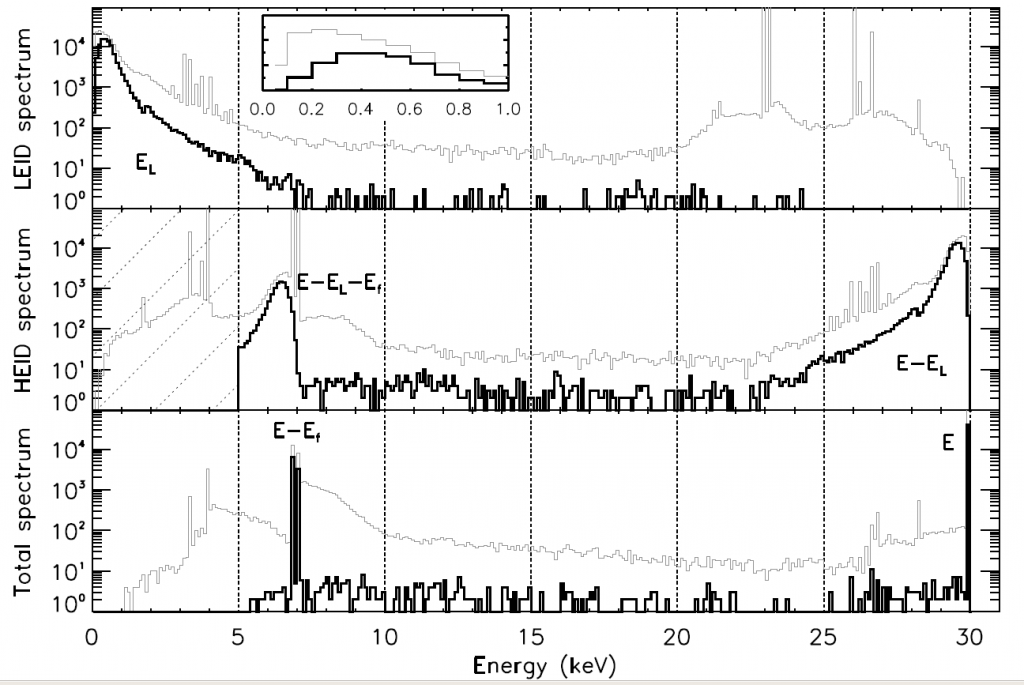
The simulation setup consisted of a Silicon Low Energy Imaging Detector (LEID) with a thickness of 450 microns, separated by 2 cm from a Cadmium Telluride High Energy Imaging Detector (HEID) of thickness 2 mm. photons of energies from 20-100 keV were incident on the detector, repeated for several different polarization angles. Figure 4 shows an example of spectra for incident E = 30 keV photons, with several important peaks. The
peak in the LEID spectrum corresponds to the scattering event, and the
peak in the HEID spectrum is the absorption event in the second detector. Finally, there is another peak at
which is caused by a Cadmium fluorescence photon escape from the detector; this occurs when a photon ionizes the Cadmium and electrons in higher orbitals fill in the hole left behind, radiating with lower energy than the incident radiation.
If polarized radiation is incident on the detector, Compton scattering predicts a square-cosine modulation of the signal as a function of azimuthal angle. Figure 5 shows azimuthal histograms of scattered photons, from which the polarization angle of the incident light is easily found. When the light is unpolarized, no such angular dependence exists.
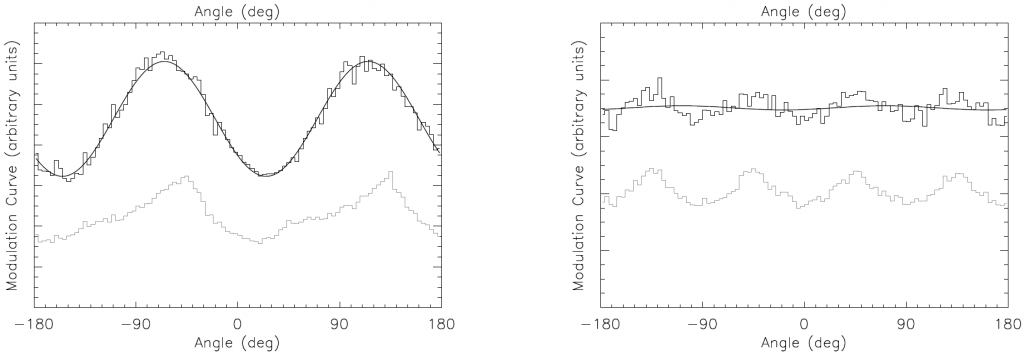
Figure 5: Modulation curves for polarized light of 25 degrees (left) and unpolarized light (right). Notice that the minimum occurs at 25 degrees as expected for polarized light.
From these simulations, the authors were able to determine the sensitivity of a generic X-ray polarimeter to various polarization angles. They found a peak in the quality factor (a measure of the sensitivity) as a function of the maximum scattering angle, which appears to be characteristic of this instrument design. Unfortunately, however, the main result is that the stacked imager design is not intrinsically very sensitive to polarization due to the low probability of scattering by the first detection plane, and that the fundamental sensitivity of this design could only be improved by factors of a few.



Dear Kirit,
thank you for the highlight of our work!
I would like just to add to your review that, although stacked polarimeters have a low sensitivity, instruments dedicated to measure polarization with good sensitivity do exist. If you are interested, a nice review of the different techniques and designs is in the “X-ray Polarimetry: A New Window in Astrophysics” book edited by Cambridge University Press.
Cheers,
Fabio