• Title: An upper limit to the velocity dispersion of relaxed stellar systems without massive black holes
• Authors: M. Coleman Miller & Melvyn B. Davies
• First Author’s Institution: University of Maryland, College Park
It is well accepted that massive black holes exist at the centers of most, and probably all, large galaxies. To take it even one step further, the masses of these central black holes correlate with galaxy properties. At the most basic level, this means more massive galaxies have more massive central black holes. You may have noticed that I said all large galaxies have central black holes, but how exactly do we define large? This is actually a pretty tough question, and is complicated by the fact that less massive black holes are tougher to find observationally. Do stellar systems, including small galaxies and globular clusters, cease to have central black holes at a certain mass? Or do these small systems have black holes whose masses do not correlate with system properties in the same manner as they do for more massive galaxies?
Miller & Davies investigate whether low mass stellar systems may harbor central black holes using analytic arguments and simple simulations. Instead of phrasing the question in terms of the mass of the system, however, Miller & Davies investigate these possibilities in terms of the velocity dispersion of the system. The velocity dispersion is a measure of variation in velocities of stars on randomly distributed orbits, and thus a proxy for the kinetic energy of all the stars. The kinetic energy is in turn related to the mass of the system by the virial theorem.
Ready, set, core collapse
Gravitationally bound stellar systems are dense, dense enough that stars can interact and exchange energy and angular momentum with each other. This process is called two-body relaxation and is described in further detail in this post. Because of these two-body interactions, the system tends towards an equilibrium state over a period of time, known as the relaxation time. The relaxation time of a star of mass m in a system is

An image of the globular cluster M15, which has undergone core collapse and thus has a very high density core. Image credit: ESA, Hubble, NASA, APOD
In practice, systems with σ > 100 km/s have relaxation times longer than the age of the Universe, so Miller & Davies focus on systems with velocity dispersions less than 100 km/s. For a gravitationally bound stellar system, the relaxed state consists of a high density core and a lower density halo. When this relaxation state occurs, the core is at such high densities that it essentially evolves independently of the halo surrounding it and ultimately undergoes “core collapse” (e.g. Lynden-Bell, 1975). This core collapse process is observed in some globular clusters, such as M15 (shown to the left).
However, this core collapse scenario has been argued using a system of single stars, whereas many stars are formed in binary (or higher order) systems. So why is this a problem? For a binary system, the energy of the system is not only described by its bulk motion (as for a single star), but also by the gravitational binding energy of the system (remember that binding energy is negative!). This extra energy consideration can change the outcome of two-body relaxations. Consider an encounter between two single stars — all of the energy and angular momentum exchanged must affect the bulk motion of the stars. In contrast, if a binary system is involved in the encounter, the binary can harden, which means the two stars can become closer and thus have a higher (negative) binding energy, and thus inject extra energy into the system. This extra energy contribution can actually prevent core collapse. When accounting for binarity in the initial stellar population of low-mass systems, Miller & Davies find that cluster core collapse is not possible for systems with velocity dispersions lower than approximately 40 km/s.
Core collapse, now what?
In addition to arguing that systems with velocity dispersions between 40-100 km/s will undergo core collapse, Miller & Davies also investigate whether core collapse leads to the formation of a central black hole. They discuss three potential outcomes of core collapse which may lead to a central black hole on short timescales. Each scenario relies on the outcome of a process called mass segregation. Because of this process, more massive stars are more likely to tend towards the center of the cluster, which means that a large number of stellar mass black holes (5-10 times the mass of the Sun), which are the evolutionary end states of the most massive stars, will lie at the center of the cluster. Miller & Davies first consider whether these black holes could undergo a runaway merger, forming a much larger black hole; however, the authors rule this scenario out since a collision between two black holes would likely eject the remnant out of the system due to gravitational radiation.
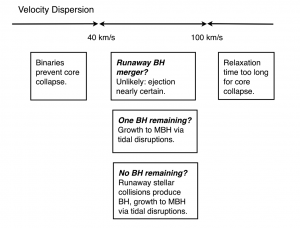
Miller & Davies figure 1. The figure summarized the paths that may (or may not) lead to massive black hole formation based upon velocity dispersion in a low mass stellar system.
Since the collisional timescale of stellar mass black holes in the core is short, all, or almost all of the black holes in the core will be ejected from the system. The authors argue that these ejections lead to the other two possible scenarios: (1) a core with no stellar mass black holes remaining or (2) a core with one stellar mass black hole left. According to the authors, this outcome is based upon whether the original number of black holes was odd or even since, as discussed in the previous paragraph, black holes collide in pairs, and are then ejected from the system. In the case that there is one black hole remaining, the authors argue the this black hole will grow on short timescales by tidally disrupting nearby stars. In the case where no stellar mass black holes remain, Miller & Davies argue that a series of stellar collisions will lead to the runaway growth of a massive star which in turn becomes a massive black hole.
In other words, Miller & Davies suggest that massive central black holes will form at the centers of small galaxies and globular clusters no matter what if these systems undergo core collapse. The potential pathways to central black hole formation are summarized in the figure to the right. It is important to note, however, that central black holes formed via these processes may not follow the same system-black hole scaling relations as the black holes found in higher mass systems. Furthermore, Miller & Davies point out that their findings do not rule out massive black holes in lower velocity dispersion systems.




