• Title: Detection of Gravitational Redshift on the Solar Disk by Using Iodine-Cell Technique
• Authors: Yoichi Takeda and Saturo Ueno
• First Author’s Institution: National Astronomical Observatory of Japan, Tokeyo, Japan.
In 1916, Albert Einstein published his final version of the theory of General Relativity and revolutionized our current understanding of physics. One prediction of general relativity (GR) is that because of the way that gravity affects time, the frequency of electromagnetic radiation (light) emitted at the solar surface should decrease as it escapes the Sun’s gravitational potential well, i.e., the solar spectrum should appear gravitationally redshifted. Surprisingly, although this was one of the first predictions made by Einstein, it had yet to be definitively tested until now according to this recent paper by Takeda and Ueno. Why not? The predicted degree of redshift is tiny – roughly 600 m/s – and thus it has been difficult to disentangle the GR effect from other mechanisms that affect the shape and centroid (the mean wavelength of the distribution of photons) of spectral lines. For example, the surface of the Sun is constantly in motion – it is bubbling with convective granules as seen in Figure 1. It is also differentially rotating – because the Sun isn’t solid, its layers don’t move all together. In an idealized world, a spectral line would only be detectable at one particular wavelength, making its position trivial to determine. Allow for some realistic physics, and the line becomes broadened by the random thermal motions of the emitting particles, redshifting some photons and blueshifting others by the Doppler effect, but keeping a nice, well-defined gaussian shape. Now add in all of the convective motion, along with the complication that we can see photons coming from many different depths and therefore moving at different speeds, and the shape of the line becomes more complex, making it harder to infer what its centroid would be in the absence of these extra factors. The authors undertake the most vigorous search for this phenomenon to date, empirically demonstrating that the solar spectrum is indeed gravitationally redshifted by about 600 m/s as predicted by General Relativity.
Are you saying there was no good evidence for gravitational redshift until now?
While the search for a gravitational redshift in the Sun has been delayed by technical challenges, other experiments have also gone after precision measurements of gravitational redshifts. The first successful laboratory test was the Pound-Rebka experiment in 1959. Pound, a physics professor at Harvard, and Rebka, his PhD student, devised a way to measure gravitational redshift (or blueshift, in this case) by balancing it against a known Doppler shift. GR predicts that photons will be redshifted moving away from a gravitational potential well, i.e. the gravitational field created by a massive object like the Sun or the Earth, and blueshifted in the reverse process of falling into a potential well. In their setup, Pound and Rebka essentially moved an emitting source upwards as it sent photons downwards to a receiver. The upward motion would introduce a Doppler redshift, while, according to general relativity, the photons would become blueshifted, gaining energy as they traveled deeper into the Earth’s gravitational potential well. The trick was that only one wavelength of light was emitted, and thanks to quantum mechanics, the receiving block of material could only absorb photons of that same initial wavelength. When photons were absorbed, Pound and Rebka knew that they had introduced just the right Doppler shift to perfectly balance the gravitational blueshift, and hence could show that Einstein’s claim was correct.
The Pound-Rebka experiment was followed by other close-to-home tests. In 1976, Gravity Probe A demonstrated that atomic clocks run faster in space than on Earth, a testament to gravitational time dilation. Gravitational time dilation is closely related to the phenomenon of gravitational redshift. Think again about a photon climbing out of the Earth’s potential well, i.e. traveling into space. As mentioned above, it will become redshifted, which means it will have a lower frequency, or, thinking of light as a wave, peak in intensity less often. However, nothing has really happened to the photon – it’s the same light – so time itself must be passing more quickly, otherwise we would measure the same (larger) number of peaks per second as we did on the ground. GPS satellites account for this effect, too – if they didn’t, they wouldn’t be able to accurately communicate with your GPS!
There is also compelling evidence for gravitational redshift in other stars, most notably Sirius B. Sirius B is a white dwarf, a stellar remnant with density almost one million times higher than the Sun’s. Imagine cramming the entire mass of the Sun into an object about the size of the Earth. These extreme conditions make GR effects much more pronounced than they are on the Sun, and therefore easier to detect. Numerous groups have measured gravitational redshift for Sirius B, including Popper et al. in the 1950’s and Greenstein et al. in the 1970’s. Nonetheless, these observations are no cakewalk – spectral lines of white dwarfs can be quite broad and faint, making it hard to measure line centroids accurately for comparison with those of known spectral lines.
Uncovering gravitational redshift in the solar spectrum
Although general relativity has these many victories, some astronomers were still bothered by the lack of convincing data to support Einstein’s early prediction for the Sun. Takeda and Uedo tackle this problem with careful consideration of the spectral line shape and good statistics. Using the Domeless Solar Telescope at the Hida Observatory of Kyoto University, they obtained spectra of 3,000 different positions on the solar disk. To avoid even small instrumental uncertainties, they placed an iodine-cell (a tube of iodine gas) in front of the detector while collecting their observations. Iodine gas has a unique spectral signature (like all molecules) and a plethora of thin spectral lines; thus, it can be used for high-precision calibration and then easily subtracted from the real data.
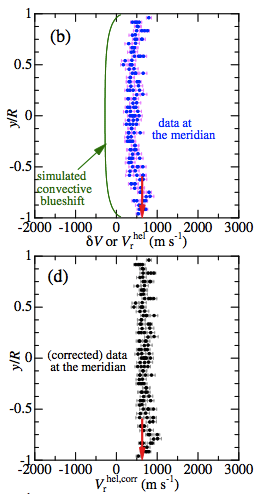
Figure 3: Average velocity shifts of the solar spectrum as a function of position north/south along the meridian. The bottom panel shows the data after the convective correction (in green on the top panel) has been applied. The red arrow shows the gravitational redshift predicted by GR (633 m/s), which is in good agreement with the mean redshift of 698+/-100 m/s from the data.
As mentioned earlier, various effects like convection of solar granules (Figure 2) can change the shapes of the observed spectral lines, masking the GR signature; thus, it is necessary to characterize and remove these effects. Photons emitted as the hot plasma moves upward into a granulum are blueshifted, and those emitted as the plasma cools and falls back down between granules are conversely redshifted. Because the bright, upward-moving granules dominate the spectrum, the net result is a blueshifted spectral line. The magnitude of this effect depends on the depth at which the majority of the photons are emitted; since the convective flow is faster at the bottom of the cell and slows near the surface, photons coming from deeper inside the photosphere will be more blueshifted. In addition, other studies indicate that this blueshift weakens going towards the projected edge or limb of the Sun. While the exact explanation for this solar limb effect is not well understood, it is thought to relate to horizontal motions of the solar surface and the fact that we can’t see as far into the interior of the Sun when looking near its edge. (The second piece is closely tied to limb darkening.) The authors use theoretical model atmospheres to calculate the blueshift from convection for each observed position, then add in empirical corrections to account for the solar limb effect.
While the authors obtained spectra from positions all across the Sun’s disk, they chose to focus on the points near the meridian where there is no additional Doppler shift from the solar rotation. These velocities, corrected for the Doppler shift introduced by the Earth’s rotation about its axis, are shown in Figure 3. The modifications discussed above are shown by the green line in the top panel, and removed in the bottom panel. The red arrows indicate the expected gravitational redshift, and clearly agree with the observations. The authors quote a mean redshift of 698 m/s with an uncertainty of up to 100 m/s, while general relativity predicts a gravitational redshift of 633 m/s. The full dataset suggests similar, consistent results, although it is complicated by a additional Doppler shifts from the Sun’s rotation. This is the first definitive demonstration of this prediction of GR using our nearest star, one that Einstein made nearly 100 years ago. Once again, GR continues to stand the test of time as the best theory of how gravity works in the Universe.