• Title: Second Season QUIET Observations: Measurements of the CMB Polarization Power Spectrum at 95 GHz
• Authors: The QUIET Collaboration
• First Author’s Institution: Kavli Institute for Cosmological Physics, The University of Chicago
Since its discovery in 1965, the Cosmic Microwave Background (CMB) has been a treasure trove of information about the universe. The CMB is snapshot of the universe at 380,000 years of age. Its measurement essentially confirmed the Big Bang theory, and since then has told us the values of many parameters that describe our universe, including its curvature. This paper describes an experiment designed to confirm or refute the leading theory about what happened in the instant of time after the Big Bang.
Inflation and the CMB
The theory of inflation is absolutely critical to our understanding of modern cosmology. The idea is that in the very beginning of the universe, around 10^-36 seconds after the Big Bang, the universe experienced a violent exponential expansion in which its volume increased by a factor of about 10^78. While it sounds farfetched, inflation solves many cosmological problems: it explains why we don’t see magnetic monopoles, why the CMB is so uniform, and why the universe has a flat geometry. Since it was proposed over 30 years ago, almost all of inflation’s predictions have been detected. The last, unobserved prediction is that quantum fluctuations generated a gravitational wave background in the early universe. If detected, it would be a “smoking gun” for inflation, and could even tell us how powerful the expansion was. But how could we detect these inflationary gravitational waves?
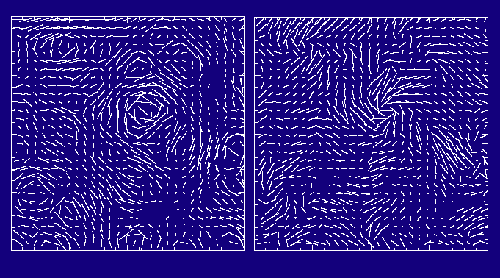
It turns out that the CMB is polarized due to Thomson scattering, most of which is due to density fluctuations in the early universe. A much smaller amount of polarization should be caused by gravitational waves — and luckily, these two sources give rise to different polarization patterns. In analogy to electromagnetism, a polarization map can be decomposed into two orthogonal bases, or modes: an “E-mode” which looks like a gradient, and a “B-mode” which looks like a curl (see Figure 1). E-modes, which were detected 10 years ago, can be generated by both density fluctuations and gravitational waves. B-modes, which remain unseen, can only be generated by gravitational waves. So if we make a map of the CMB polarization, decompose it into E and B, and see nonzero B-modes, we have detected the gravitational wave background and have thus confirmed the existence of inflation!
The QUIET Instrument
The Q/U Imaging ExperimenT (QUIET) was built with the purpose of detecting B-modes. Located on the Chajnantor plateau in Chile’s Atacama desert, a site known for excellent radio and microwave seeing, it observed from 2008 to 2010 at 43 GHz and 95 GHz. This paper covers the second season of observations with the 95 GHz data (the 43 GHz data were released in a previous paper). The telescope is a 1.4 meter Dragonian reflector (Figure 2) which illuminates a focal plane populated by polarization-sensitive radiometers.

Figure 2: The QUIET reflector and cryostat featuring a side-fed Dragonian design. The focal plane is inside the cryostat.
Unlike many other CMB experiments, QUIET uses coherent detectors which preserve the wave nature of light (most experiments employ bolometers, devices which which are only sensitive to intensity and not phase). This allows the detectors to simultaneously measure both components of the linear polarization of light, unlike polarization sensitive bolometers. The QUIET detector modules are Monolithic Microwave Integrated Circuits (MMICs), which are essentially “detectors on a chip.” This technology allows a large number of radiometers, each the size of a postage stamp, to be packaged into a focal plane at low cost (see Figure 3). Since more detectors equals more sensitivity, this is a great innovation!

Figure 3: QUIET MMICs. Left: The first 90 GHz module. Top right: The exterior of a 90 GHz module. Bottom right: The interior of a 40 GHz module. This new "detector on a chip" technology makes it cost-effective to deploy large numbers of radiometers in detector arrays.
Power Spectra and Limits on Inflation
After observing for the CMB for 5337 hours at 95 GHz, QUIET made polarization maps of four regions on the sky. These maps were then decomposed into E and B maps, and then into angular power spectra: plots showing how much the sky signal varies as a function of angular distance. The top panel of Figure 4 shows the E spectrum. As expected, nonzero E-modes are clearly seen (and the first three acoustic peaks match well with standard cosmological theory).
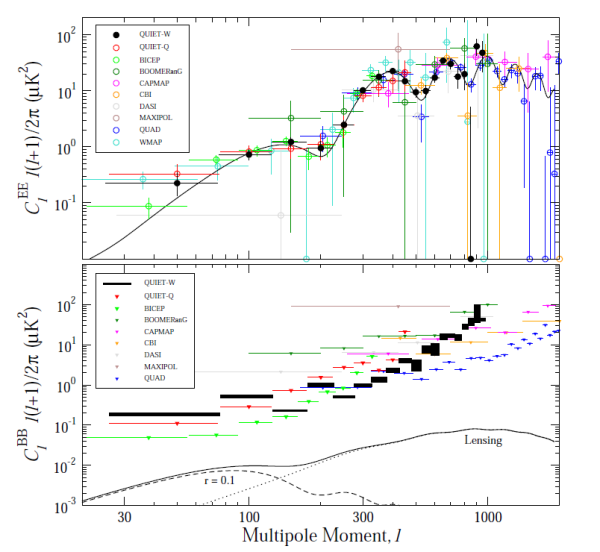
Figure 4: QUIET E-modes and B upper limits. The QUIET data points are in black. The x-axis denotes angular scale; low values of l correspond to large angles on the sky. In the B mode plot, the dashed line shows the theoretical power spectrum for B modes at r = 0.1 (it could be much lower). The dotted line shows the secondary effect of gravitational lensing, which turns E-modes into B-modes at small angular scales. The solid line is the sum of the two.
B-modes were not seen in the data. The standard measure of inflation is the tensor-to-scalar ratio, r, the ratio of the amplitudes of the gravitational waves to density perturbations in the early universe. A large value of r means that gravitational waves in the early universe was large, and thus that inflation was strong. Since the B spectrum is consistent with zero, it is not possible to give a confidence interval for r; instead, CMB experiments quote upper limits on the strength of inflation. QUIET’s data reduction returns two upper limits: r < 2.7 or r < 2.8, depending on the pipeline used. As seen on the bottom panel of Figure 4, many experiments are now pushing down the limits on B-modes. If r is in the range of 0.01, as is predicted by some inflationary theories, the next generation of experiments which feature many more detectors should be able to find it!



Dear Kirit:
I am astounded to learn of QUIET, as I’d been led to believe that Only the Planck sat was capable of detecting the B-modes. My understanding is that Planck will make an announcement soon. What value of r will it take to invalidate inflation ? As you probably know, the cyclic model predix no significant B-modes.
Thanx,
Jimbo
Hi Jimbo – it turns out that Planck is not optimized for large angular scale B-modes, which is where the inflationary signal should peak. It is instead optimized for high-resolution temperature and E-mode detection, and lacks the sensitivity needed for low r limits. In fact there are many ground-based B-mode experiments: QUIET, EBEX, ABS, BICEP2/Keck (on which I work), to name a few. As far as I know there is no lower limit to the amplitude of inflationary gravitational waves — but the simplest inflationary models suggest a value of r that should be detectable with current-generation experiments.
Thanx for that info. Guess I’m a bit stunned. How could the Planck sat possibly be inadequately designed to detect B-modes ? They have been touting this B-mode measmt. capability for 4 yrs now. & I understand it’s critical to measuring the mass of the Inflaton and discriminating between Inflationary v. Cyclic Universes. That would be like the LHC being built unable to detect the Higgs !
I can see it not being optimized for B-m, but not so swamped by noise that it has no chance.
Indeed, the answer may already have been found. Wiki sez an announcement from Planck sat org of `Cosmo.Significance’ is due early this year.