Title: Iterated Prisoner’s Dilemma contains strategies that dominate any evolutionary opponent
Authors: Bill Press, Freeman Dyson
First Author’s Institution: Department of Computer Science and School of Biological Sciences, University of Texas at Austin
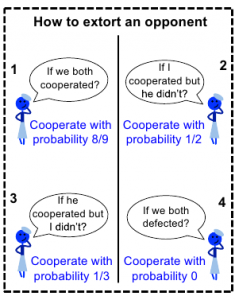
A schematic diagram of one of the newly discovered extortionist strategies for winning the Prisoner's Dilemma. This strategy ensures the player twice the score of his opponent above a threshold. From Stewart & Plotkin (2012), Figure 1.
The worst has happened: you’ve been caught! So has your conspirator. The police tell you you’re facing a year in prison, but you know they don’t have enough evidence to hold you, so you and your friend should just get a slap on the wrist. The only problem is that your friend might rat you out. If he does, you’ll get the full sentence and he’ll go free. You could decide to rat him out, but if you both confess you’ll each get a moderate sentence. If only you knew what he was thinking…
So what should you do? Of course, if you could communicate, you should definitely choose to both stay silent. But given that you’re kept apart, the best way to guarantee a short sentence for yourself (not worrying about your partner) is actually to confess.
Now what if you get caught again? Can you choose a better strategy knowing what your opponent did the previous time? What if you’re caught N times?
These are the questions Robert Axelrod posed in 1979, when he organized a famous tournament to determine the best strategy for facing this so called Prisoner’s Dilemma. The results were groundbreaking in the field of game theory and had implications throughout science, from evolutionary biology to economics. His fundamental conclusion, encouragingly, is that it pays to be nice: depending on your opponents strategy, you’ll probably do best by never ratting him out unless he ratted you out in the previous round (this is known as Tit-for-Tat). You can listen to an excellent discussion of Axelrod’s findings on Radiolab.
But new work published in May turned this 30-year-old and long-accepted result on its head. Press & Dyson (2012) show that there exist a family of “zero-determinant” strategies that trounce Tit-for-Tat. Perhaps even more surprisingly, these strategies allow you to dictate to your opponent what his score will be no matter what strategy he implements. And that’s not all — they also show that it doesn’t pay to have a long memory, as you can always achieve the same outcome by looking only at your opponent’s single previous move. The game can therefore be described as a Markov chain.
Press & Dyson’s paper is highly mathematical, while Stewart & Plotkin have written a more accessible summary of their work. They explain the strategy using the diagram above: after seeing his opponent’s move, the player chooses his next move according to fixed probabilities for each of the four possible scenarios. You can play the Prisoner’s Dilemma against the new strategies online to see them in action.
How is it possible that this new family of solutions went unnoticed in the ~60 years since the Dilemma was first posed at RAND in 1950? Press and Dyson discuss this at the Edge website. Press says he only discovered the solution when he wrote a computer simulation that had a seemingly-sound, but critically flawed, assumption: that each player’s score will depend on the strategy he uses. When the simulation encountered one of the new family of solutions, which enforce scores regardless of the opponent’s strategy, his computer crashed. It took the mind of Freeman Dyson, Press says, to elegantly generalize the solution he discovered.
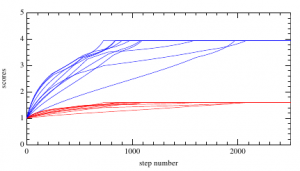
Simulated results of a Prisoner's Dilemma game between an extortionate player (blue) and a traditional, evolutionary player (red). Blue's superior strategy enforces the same score to be reached regardless of the adaptations by red. From Press and Dyson (2012), Figure 3.
While it seems that overturning Tit-for-Tat implies that it no longer pays to be nice, Press wrote on Edge that it actually suggests “a world in which diplomacy trumps conflict.” If both players have the power to enforce scores on the other, they in fact have the ability to guarantee the maximum possible outcome for both of them. In contrast, when both players use the Tit-for-Tat strategy, the score they achieve is not necessarily mutually beneficial.
As an Astrobites reader, you might wonder what all of this has to do with astronomy. First, it’s worth noting that Press and Dyson each have a long list of accomplishments in the field (you might recognize their names from the Press-Schechter formalism and Dyson spheres, for example). But more importantly, this new discovery should encourage astronomers — and all other scientists — to re-examine long “solved” problems in their discipline.
What if Type Ia supernovae don’t come from white dwarfs? And what if the first stars weren’t actually zero metallicity? These scenarios seem frankly implausible given the evidence to the contrary. But this was the essence of the situation 15 years ago, when two groups revolutionized cosmology by discovering that the expansion of the universe is accelerating. What can we learn from challenging basic, well supported assumptions?
In a recent essay, Avi Loeb has suggested that society can nurture such discoveries by giving individual scientists the freedom to include risky research in their academic portfolios. But it’s one thing to devote your time to widely debated, if not widely accepted, ideas such as MOND or gravitational wave detection. It’s quite another to look back at a seemingly solved problem and, somehow, arrive at a remarkably fresh perspective. Press & Dyson remind us that the latter tactic is possible.
