Observational Signatures of Accretion Induced Collapse of White Dwarfs

This relationship occurs for an object that is in hydrostatic equilibrium and supported by non-relativistic electron degeneracy pressure. Once the WD reaches the Chandrasekhar mass of ~1.4 solar masses, the electrons become relativistic and the WD is unstable. This causes a substantial amount of matter in the WD to undergo runaway nuclear reactions, producing enough energy to unbind the WD and result in a supernova explosion. The second possibility, which likely occurs for the more massive and therefore denser Oxygen/Neon/Magnesium (O/Ne/Mg) WDs, is accretion-induced collapse. As the O/Ne/Mg WD accretes matter, electron capture can remove the pressure support due to degenerate electrons and  results in neutronization via the reaction:

Once the WD Chandrasekhar mass limit is reached it will collapse to form a neutron star (NS). Furthermore, the resulting NS  may be highly magnetized because the magnetic field is compressed as the star shrinks and it will also be a fast rotator due to the addition of angular momentum from accretion and collapse. This formation mechanism may be able to explain millisecond pulsars (rapidly rotating NS), magnetars (highly magnetized NS), and other types of exotic objects.

After the Collapse…

The implosion of the WD into a NS will unbind material and the remnant disk will also lose mass due to heating from neutrinos (i.e., the disk is so optically thick that photons can’t escape but neutrinos can), turbulent viscous heating, and the recombination of helium from free nucleons. The result is a subluminous supernova. The optical signature of such an event is quite short, lasting for about a day – this makes such an event difficult to detect.

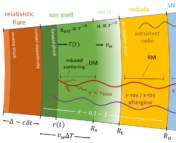
About a tenth of a solar mass or less of material will be ejected from the newly formed NS during the implosion, and the ejected material will be moving quite fast, typically at a speed of ~0.1 c. At this speed, the ejecta will have a kinetic energy on the order of  ~10­_­⁵⁰ erg.  The ejecta will expand freely until it sweeps up a mass comparable to its own, which for the numbers just discussed and an ISM density of 1 proton per cubic cm is ~16 yrs. Therefore, the authors assume that the ejecta will be in a free-expansion phase (i.e., moving at a constant velocity) throughout the period of interest.

The magnetar will lose energy as it spins down and thus inject energy into its surroundings via magnetic fields and the particles from its winds that are accelerated to relativistic speeds. This energy loss will power a pulsar wind nebula (PWN). Within the PWN, the electrons from the wind will be accelerated to relativistic speeds at the location where the ram pressure of the pulsar wind is balanced by the pressure of the PWN. This location is much smaller than the actual size of the PWN and so the PWN is mostly filled with relativistic electrons which are accelerated radially by the magnetic fields. This leads to synchrotron emission. Not only will these electrons emit photons and cool but they can also absorb them too – this is known as synchrotron self-absorption.

Detecting Such an Event…

Okay, so detecting such an event with an optical telescope may be quite difficult, but luckily for astronomers synchrotron radiation is at radio wavelengths and typically lasts for a while as the remnant expands.

The rate of synchrotron self-absorption depends on the frequency, so the flux will peak at the frequency where the medium becomes optically thin due to synchrotron self-absorption. This peak frequency depends on both the magnetic field strength and will shift to lower frequencies as the magnetic field strength decreases due to the expansion of the PWN causing the peak to shift to lower frequencies as time increases. The authors find that synchrotron cooling will dominate and thus be detectable ~months after the collapse as shown in the figure below.

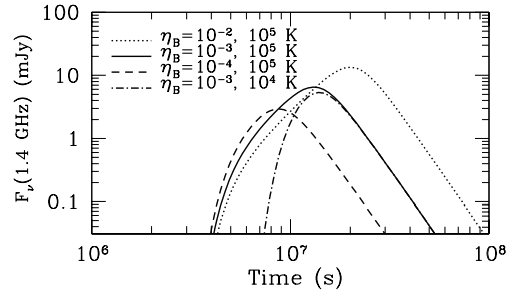
This figure shows the time dependent flux due to synchrotron cooling of the relativistic electrons for ν=1.4 GHz, assuming the object is at a distance of 100 Mpc. Here describes η­B the fraction of the magnetar luminosity that goes into magnetic fields. A lower η­B corresponds to a smaller magnetic field strength and thus the peak of the curve is shifted to later times.

The peak of the emission is strongly dependent on the initial spin rate and magnetic field strength of the magnetar since its energy loss, and thus PWN properties, depend on these factors. The figure below shows that the peak flux can vary by several orders of magnitude for a wide range of magnetic field strengths and spin rates typical of rapidly rotating magnetars. The authors expect that if the emission is above ~1 mJy and has a duration of about 3 months, then there should be at most 4 observable events per year within a volume of 100 Mpc.

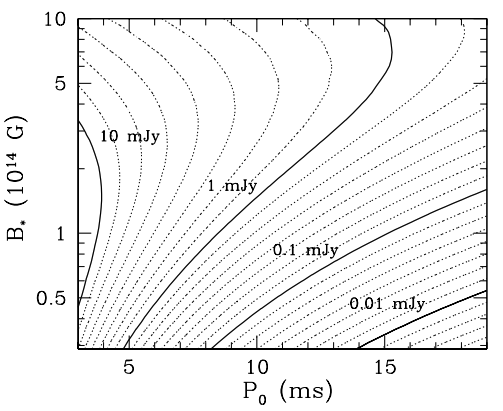
This figure shows the peak flux at 1.4 GHz at 100 Mpc as a function of the initial spin period and magnetic field strength of the newly formed magnetar.

• About the Author

About Anna Rosen

I am a graduate student at the University of California, Santa Cruz in astronomy and astrophysics. I obtained my Bachelor’s degree in physics and astrophysics at the University of California, Berkeley. My research interests are in theoretical stellar astrophysics with an emphasis on the formation of massive star clusters and massive stars.