Authors: Sean T. McWilliams, Jeremiah P. Ostriker, Frans Pretorious
First Author’s Institution: Princeton University Dept. of Physics
The Era of Gravitational Wave Astronomy
The detection of gravitational waves is one of the next major frontiers in physics. Predicted by Einstein’s general theory of relativity but not yet directly confirmed experimentally, many cutting-edge facilities have been and are being built with the singular goal of discovering their existence. It is possible, however, that an Earth-based experiment will not be the first to confirm gravitational waves. Instead, astrophysicists using pulsar timing arrays – Galaxy-wide networks of spinning neutron stars – may be on the verge of this groundbreaking discovery. In today’s paper, the authors argue that new calculations for the number of supermassive black hole mergers – a prime source of gravitational waves – imply a signal that may be measurable by pulsar timing arrays with current data.
What are Gravitational Waves?
According to general relativity (GR), the presence of matter causes the fabric of spacetime to curve, and the motion of massive objects causes this curvature to change with time. GR predicts that an accelerating object should radiate gravitational waves (GWs), just like how an accelerating charge radiates electromagnetic waves. Gravitational waves are essentially “disturbances” in the fabric of spacetime; the effect of a passing GW on a circle of stationary test masses is to cause them to oscillate orthogonally, with the particles along one axis and then the other being displaced alternately inward; see this animation for a nice visualization of the effect. Since gravity is much, much weaker than the other fundamental forces of nature, gravitational waves have incredibly small amplitudes. Even from the strongest sources of GWs, the effect on test masses is expected to be so small as to be almost unmeasurable. (For a much more comprehensive description of GWs, see this excellent website).
Gravitational Wave Detectors
To have even a faint hope of detecting the weak gravitational wave signal, some of the most ingenious and sensitive experiments ever designed are now in operation. One is the Laser Interferometer Gravity Observatory (LIGO), which consists of two 4 km long arms along each of which a laser is reflected back and forth to measure the position of test masses to an accuracy of one part in 1020. No gravitational waves have yet been discovered, but an upgrade to Advanced LIGO will increase the sensitivity by another factor of 10 (and thus the accessible volume by a factor of 1000) by the end of the decade – theoretically enough to detect a few sources of gravitational radiation per year. But, argue the authors of the paper discussed here, another “experiment” may beat LIGO to that elusive first detection: pulsar timing arrays (see Figure 1).
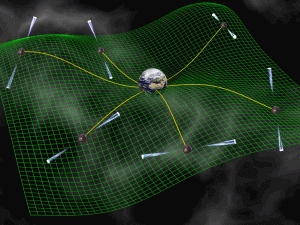
Figure 1: Artist’s conception of a pulsar timing array. The gravitational wave background, depicted as a warping of the grid in this image, induces correlated timing variations in pulsars distributed throughout space. Image credit: David J. Champion
Using pulsars as precise astrophysical clocks
Pulsars are a subclass of neutron stars, the extremely dense, degenerate, compact remnants of very massive stars. Pulsars have extremely strong magnetic fields and rotate very rapidly, and their emission is beamed along the magnetic axis. Since the rotational and magnetic poles are typically not perfectly aligned, this beam sweeps across the sky like a lighthouse, and pulsars are detected at radio (and sometimes x-ray or gamma ray) wavelengths as regular pulses each time the beam sweeps by our line of sight. For an more complete review of the general properties of pulsars, see this Astrobite.
It also turns out that pulsars are incredibly accurate and stable clocks, particularly the highly rapidly rotating subclass known as millisecond pulsars. The rotational frequency of a pulsar decreases over time as it loses energy, but millisecond pulsars are in binary systems and are spun back up via transfer of angular momentum from their companion. Perhaps stable is not a strong enough word: as an example, the measured period of the millisecond pulsar PSR B1937+21 is 1.5578064688197945 +/- 0.0000000000000004 milliseconds. Yes, that’s correct, the measurement is accurate to 10-18 seconds! Knowing the period so exquisitely translates into the ability to predict the arrival time of each pulse to the same level of accuracy – and thus, to be able to detect minute deviations in this arrival time. If gravitational waves pass along the line of sight, the effective path length of each pulse will be slightly altered by these waves, and thus the arrival times will fluctuate in a characteristic fashion based on the gravitational wave amplitude and frequency.
It is expected that due to the combined effects of supermassive black hole (SMBH) mergers across the Universe, there should be a “background” of low-frequency gravitational waves pervading all space, and thus all lines of sight will include some GW interaction. One can measure the overall variation in arrival times (called the “timing residuals”) for a single pulsar and thereby place an upper limit on the GW background. However, since this background is expected to be homogenous and isotropic, there should also be correlations in the variations of timing residuals between multiple pulsars with known positions. This is where the concept of an “array” comes in: if the arrival times of light from many pulsars spaced across the Galaxy can be accurately compiled over a long period of time, these correlations – and thus gravitational waves – can be detected. Several groups, including NANOGrav and the European Pulsar Timing Array have been taking regular measurements of millisecond pulsars for the past several years and have already begun to place upper limits on the gravitational wave background, but have not yet achieved a definitive detection.
So, why are pulsar timing arrays going to win?
McWilliams et al. argue that the predicted gravitational wave signal detectable by pulsar timing arrays has been underestimated in previous work. Why? Well, the estimated level of the GW background discussed above relies on many uncertain factors: the space density of SMBH mergers, the number of SMBHs of various masses, and the timescale for such mergers to occur. Since there has been very little star formation since a redshift of z=1 and yet significant galaxy growth, galaxy mergers must have played an important role in this growth. Previous efforts generally relied on dark matter-only simulations to predict merger rates and timescales. In this paper, the authors add a stellar component to satellite galaxy halos, and this greatly decreases the time it takes for the satellite to fall completely to the center of the host galaxy due to dynamical friction. Galaxy mergers lead to mergers of their SMBHs, and thus the decreased infall time for satellites implies that SMBH merger rates may be underestimated in dark matter-only simulations. The authors express the merger rate as a probability distribution, then perform Monte Carlo simulations to estimate the GW signal hc. Their results are shown in Figure 2.
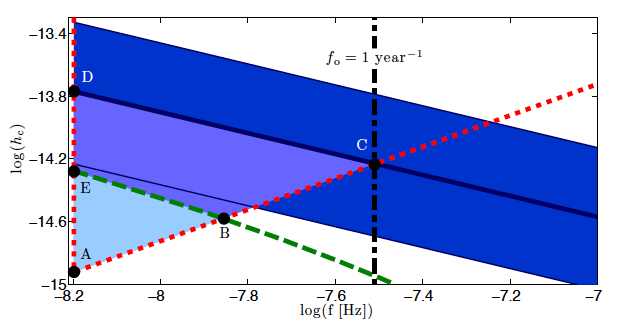
Figure 2: Predicted gravitational wave signal (or “strain”, hc) as a function of GW frequency. The dark blue band represents the authors’ predicted background signal from SMBH mergers, and the medium blue triangle with vertices ACD shows the region of the plot in which GWs could be detected with current pulsar timing array data – suggesting that GWs may already be detectable!
The bottom line, argue McWilliams et al., is a predicted gravitational wave signal that is greatly increased from previous estimates, and thus a higher signal-to-noise ratio for pulsar timing arrays – enough to perhaps detect gravitational waves in current data! Since signal-to-noise also increases with observation time, the authors predict that, given their calculations, timing arrays should detect gravitational waves by 2016 at the latest. A confirmed detection would be no less than revolutionary, confirming one of the final untested predictions of GR and ushering in the era of gravitational wave astronomy. And it may be just around the corner!




Trackbacks/Pingbacks