- Title: Visualizing Spacetime Curvature via Frame-Drag Vortexes and Tidal Tendexes
- Authors: David A. Nichols, et al.
- First Author’s Institution: Caltech
Quick, draw the magnetic field generated by this solenoid:
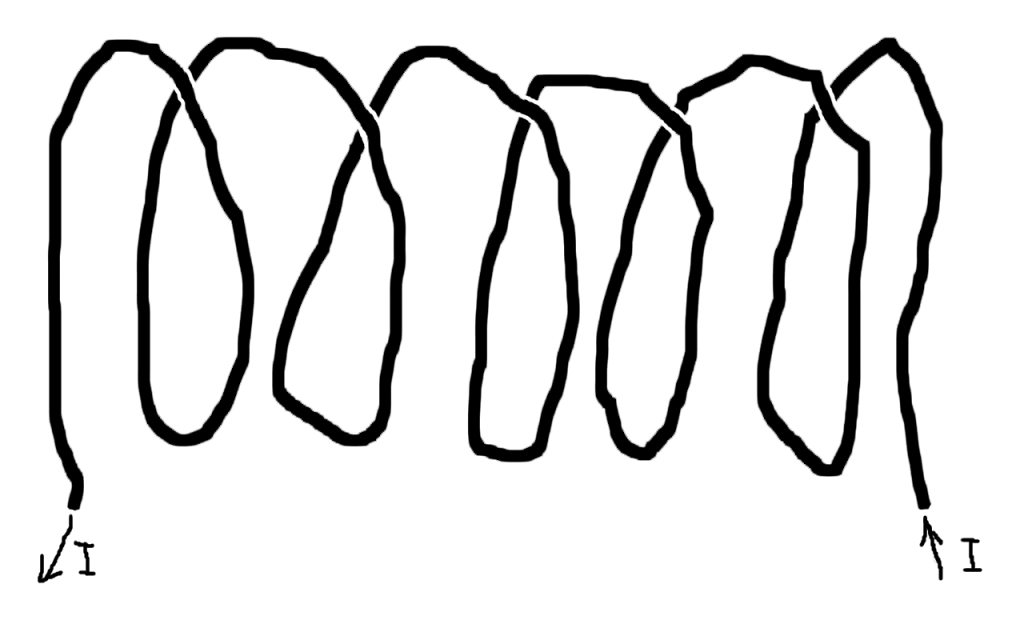
Figure 1: Solenoid: a tightly wound spiral of wire carrying an electric current. (Click on the image to see the B-field.)
Times up! Now raise your hand if you actually solved Maxwell’s equations for this. Okay put your hand down; that’s impressive, but seriously…
Perhaps you solved this canonical magnetostatics problem by remembering a diagram from your introductory electromagnetism course. If you didn’t remember, maybe you solved it in a sequence of pictures, starting with the B-field lines near a straight wire (obeying the right-hand rule), then in your imagination, bending the wire into a loop, and stacking loops as in the figure. The B-fields for each wire superpose to make a quiver of field lines flowing from right to left through the interior of the solenoid. Either way, by remembering or deriving, you used visual thinking.
Field lines are a powerful tool for building intuition for a complex geometric object such as a 3-dimensional vector field. Magnetic field lines are paths tangent to the magnetic field vectors. The direction of the field line tells me how a magnet tends to align at that location. And the density of the field lines corresponds to the strength of the B-field.
We use field lines to visualize electromagnetism. But how do we visualize gravity? This is a problem faced by numerical relativists who simulate dynamical spacetimes around wobbling and colliding black holes. You can do a reasonable job with an embedding diagram: a 2-dimensional projection that looks like a rubber sheet. But these diagrams ignore one spatial dimension, and they only depict the attractive component of gravity. In addition to the attraction and tidal stretching and squeezing described by Newtonian gravity, Einsteinian gravity also admits twists. How do you draw all of that?
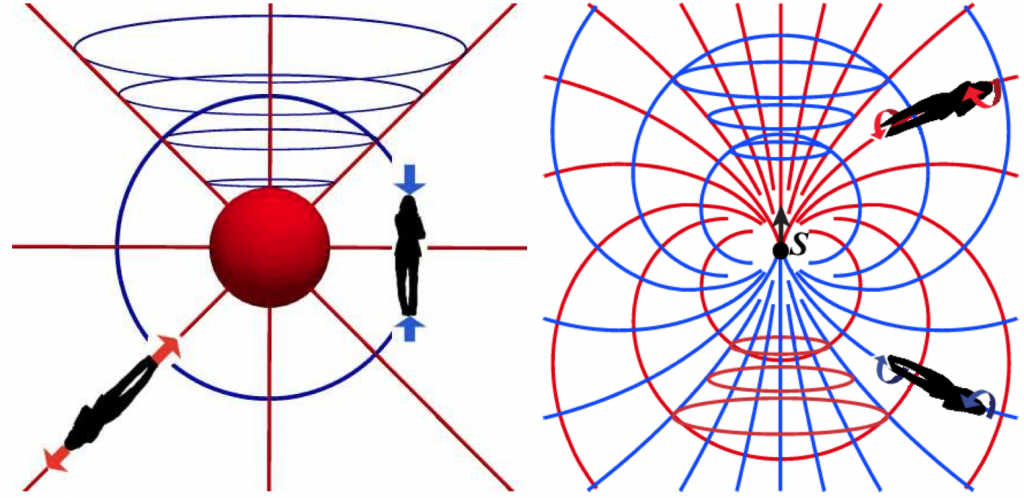
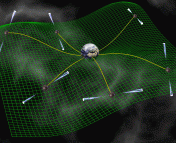
Figure 2: Simple tendex and vortex examples. Left panel: tendex lines outside a stationary spherical mass. Bodies are stretched along red lines and compressed along blue lines. Right panel: vortex lines outside a spinning point mass, with spin angular momentum oriented in the direction of the black arrow. Bodies experience a left-handed twist along red lines and a right-handed twist along blue lines.
Within the framework of Einstein’s theory, gravity manifests the curvature of spacetime. In an analogy with electromagnetism, the authors of today’s paper introduce two new tools for visualizing curved spacetime. They use the “electric” (or stretching/squeezing) part of gravity, which they call tendicity, and the “magnetic” (or twisting) part of gravity, which they call vorticity.
(A mathematical note: tendex and vortex fields are 2nd-rank tensors, similar to vectors, except they describe stress or flux information, rather than direction information. Tendex and vortex tensors are actually components of a more fundamental object, the Weyl tensor. In the same way E and B, the electric and magnetic vector fields in electromagnetism, are actually components of a more fundamental object, the Faraday tensor.)
Once you decompose a gravitational field into its tendex and vortex components, you can visualize it with tendex and vortex lines. Fig. 2 draws these for point sources of tendex (tidal) fields and vortex (twisting) fields. The tendex lines outside a spherical mass display both a stretch in the radial direction, and a squeeze in the two orthogonal directions. This is the part of gravity that raises ocean tides on the sides of the Earth facing toward and away from the Moon, and that lowers ocean tides on the orthogonal sides. The vortex lines outside a spinning mass represent the frame-dragging part of gravity that was discovered by Einstein, and confirmed by a recent experiment. A spinning mass actually drags spacetime into a spiral around it, which can be felt as a twisting force.
Now let’s put these visualizations to use. Compact binary mergers (neutron stars and/or black holes orbiting close and fast and eventually colliding) are one of the primary astrophysical sources for gravitational waves. Interferometers like LIGO and Virgo may detect such waves in the next few years. The authors close their paper by examining a toy model that captures the important dynamics of such a merger, two equal point masses in circular orbit, called a rotating mass quadrupole.
When I look at the pictures of tendex lines in the orbital plane of the rotating mass quadrupole (Fig. 3), I am struck by the visible connection between the tidal field up close to the binary and the gravitational waves far away. Up close to the binary, the red stretching tendex lines move outward radially, and the blue compressing tendex lines circle the masses. But at larger distances both blue and red lines are whipped around into tight spirals like ripples on the surface of a pond. These ripples are gravitational waves.
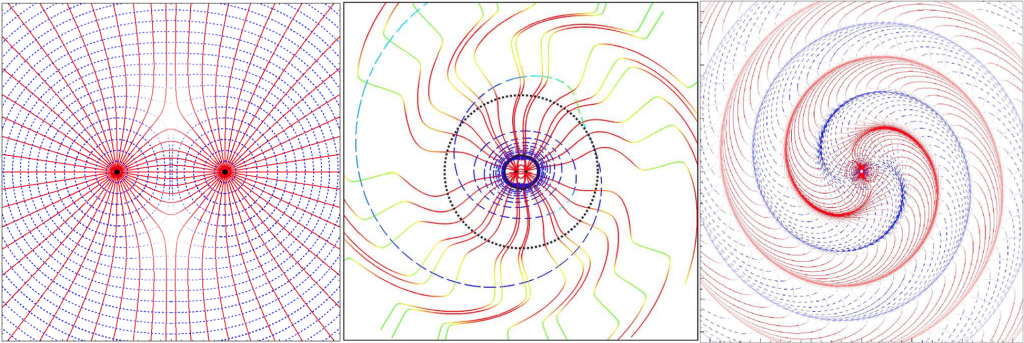
Figure 3: Tendex lines in the plane of two masses orbiting counter-clockwise. The three frames represent three levels of zoom, up close, out a ways, and really far away. The color and intensity of the tendex lines indicates the strength and sign of the tidal effect there: red means strong stretching, blue means strong squeezing, green means very little of either. Left panel (close to the binary): in the near zone the tendex lines look like those around stationary masses. Center panel (a little ways out): in the transition zone the tendex lines begin to show the imprint of the binary’s rotation. The dotted black circle represents the characteristic scale of the gravitational waves. This is the radius of transition from the radial pattern on the left to the spiral pattern on the right. Right panel (really far away): in the wave zone, the dominant quadrupolar nature of the gravitational waves is visible in the four zones of the spiral figure. If you were laying down in the orbital plane you would feel alternating stretchings (red wavefronts) and squeezings (blue wavefronts). That’s a gravitational wave!
Introducing tendex and vortex lines these authors have given relativity theorists a powerful new tool for thinking intuitively about strong gravity. From simple models (like stationary masses) we can build up an understanding of more complex scenarios (like a rotating binary emitting gravitational waves). What new physical insights lie waiting for a theorist who has trained herself to think in pictures of tendexes and vortexes?


HI Brett – looking at Figure 3 – Center panel (a little ways out): in the transition zone the tendex lines begin to show the imprint of the binary’s rotation – so is it the orbital velocity of the merging black hole that is causing the tendex lines to spiral outward as gravitational waves? meaning that because the merging or merged black holes are spinning at a significant fraction of c that this causes the tendex lines to spiral outward to become gravitational waves? Or am I misunderstanding this? I would really like to see a layman’s explanation for this outward spiraling effect…
thanks
That’s a good question! I think your explanation is headed in the right direction, speed. These black holes are orbiting at 10% the speed of light. By the time gravitational information propagates out about their current positions, they’ve already moved to new positions. How much they’ve moved gives rise to the difference between these figures. Take the left panel: in the time it takes gravitational information to propagate from the center to the edge of the panel, the binary only rotates 25deg, slightly reconfiguring the inner gravitational field. Now take the middle panel: in the time it take gravitational information to propagate from center to the dashed circle, the binary rotates 130deg, almost a full half-orbit, totally reconfiguring the inner gravitational field.
Another way to discuss this is scale of view. Imagine looking down at a rotating water sprinkler. Take a photograph up close with a narrow field of view. The stream is radial. In the time it takes the stream of water to flow to the edge of your photograph the sprinkler doesn’t rotate much. Now take a photograph from far away with a wide field of view. The stream is spiral. In the time it takes the stream of water to flow to the edge of your photograph the sprinkler has rotated many times, tightly winding the stream into a spiral.
In the figures the rays represent the direction along which gravity stretches a body. Let me drop you into the first panel, just outside the orbits of the black holes, toes in head out. The dominant effect you feel is a radial tidal force stretching you along the length of your torso. It grows and diminishes in strength very slightly twice per orbit, according to the position of the two black holes below your feet. But this oscillation is hardly noticeable over the strong, steady, radial stretch you experience due to the two black holes being nearby. Now let me drop you into the middle panel just outside the dashed line. Now the steady radial stretch is much weaker, but the oscillation due to the orbital motion is still there, in fact it’s dominant. That’s a gravitational wave! (By the way, if this were two solar mass black holes, they’d be separated by 60km and you would experience 2000 oscillations per second!)
In fact, the gravitational waves are there in the close-up picture too, they’re just swamped by the much stronger, steady, radial tidal forces.
thanks Brett – does frame dragging also play a role in this (the spiraling effect) or is frame dragging more important in creating the vortexes?
Frame dragging describes how a heavy spinning object can cause nearby spinning objects to gradually change their axis of rotation. And you’re right, that’s exactly the phenomena the vortex lines depict. Unfortunately, these figures only depict the tendex lines. I’d be very curious to see what the vortex lines look like for a binary like this!