| Gravitational Recoil from Spinning Binary Black Hole Mergers | Large Merger Recoils and Spin Flips from Generic Black-Hole Binaries | Supermassive Recoil Velocities for Binary Black-Hole Mergers with Antialigned Spins |
| Herrmann et al. | Campanelli et al. | Gonzalez et al. |
| Penn State, U TX Austin | RIT, U TX Brownsville | Uni Jena |
| published in ApJ | published in ApJ | published in Phys. Rev. Let. |
Imagine a spinning skater. She pulls her arms in a little and spins faster. She brings her arms all the way into her chest, and spins really fast, and then bam! she rockets up into the sky. Seven years ago, computer simulations revealed a configuration of two spinning black holes that merged in this way, jumping out of their orbital plane with a velocity of several thousand km/s. This is weird. It’s also important. We know that large galaxies host supermassive black holes at their centers. We also know that galaxies merge, presumably introducing their black holes to one another. If the newly formed black hole were to exit the galaxy entirely, it could carry its accretion disk with it, and be observable as a displaced core.
These papers chronicle the inadvertent discovery of this effect.
In late 2006 several numerical relativity research groups were working to characterize the effect of black hole spin on binary black hole mergers. Numerical relativists, who use intensive computing to simulate Einstein’s equations describing curved space around black holes and other dense objects, had just discovered how to model two black holes merging. This after decades of unstable codes. As an aside, the Campanelli group were at the forefront of this breakthrough, as were Frans Pretorius, and Baker et al.
With this computational success Herrmann et al., Campanelli et al., and Gonzalez et al. were independently nursing a few delicate supercomputer simulations of black holes in inspiralling orbits, with one or both of the black holes spinning at at a significant fraction of its maximum rate. The spin angular momentum of a black hole can take any value between zero and the square of its total mass. Above this, a naked bagel-shaped singularity appears outside the event horizon, which is a no-no according to Penrose’s hunch. All black holes spin, and most with large spins. These research groups were systematically simulating different configurations chosen from the many possiblities of spins and masses. Their goal was to characterize the final state of the merged remnant according to the spins and masses of the original black holes. The kinds of things they were characterizing were the final spin, the gravitational waveform, and the kick velocity.
Gravitational kicks weren’t new. Long before computer simulations had become viable, relativity theorists had known that merging black holes radiated energy, angular momentum, and linear momentum in the form of gravitational waves. If the inspiralling black holes radiated momentum preferentially in the positive x-direction, then according to momentum conservation the black holes had to recoil in the negative x-direction. Lawrence Kidder (1995) had used analytical approximations to show that such cases beamed their momentum in a circle around the orbital plane, so they wouldn’t build up a large momentum kick. Studies of nonspinning black holes had led the community to expect maximum kicks would be no more than 500 km/s, largely in the plane of the orbit. (For scale, escape velocity to leave the Solar System from Earth’s orbit is 10s of km/s; to leave the core of a giant elliptical galaxy it is 1000s of km/s.)
In early 2007, two of these groups’ simulations uncovered kicks at the very high end of the expected range. The simulation of Herrmann et al. began with their black hole spins antialigned (spinning in opposite directions) parallel to the orbital angular momentum and yielded a kick in the plane of ~500 km/s. The simulation of Campanelli et al. with one of their black hole’s spin at 45 degrees from the orbital angular momentum, and the other black hole not spinning, yielded a similar size kick, but this time out of the orbital plane!
Nobody had foreseen kicks this large out of the orbital plane. Coupling between spin momentum and orbital momentum was expected, but this coupling was huge! Campanelli et al. studied Kidder’s analytic formulae and found a term that predicted an out-of-plane kick, though not so large. They quickly saw that that term was most significant in the case of two black holes of equal mass, with spins antialigned and perpendicular to the orbital angular momentum. This would later come to be called a “superkick” configuration. For a cartoon schematic of the configuration and its subsequent evolution, see the figure below.
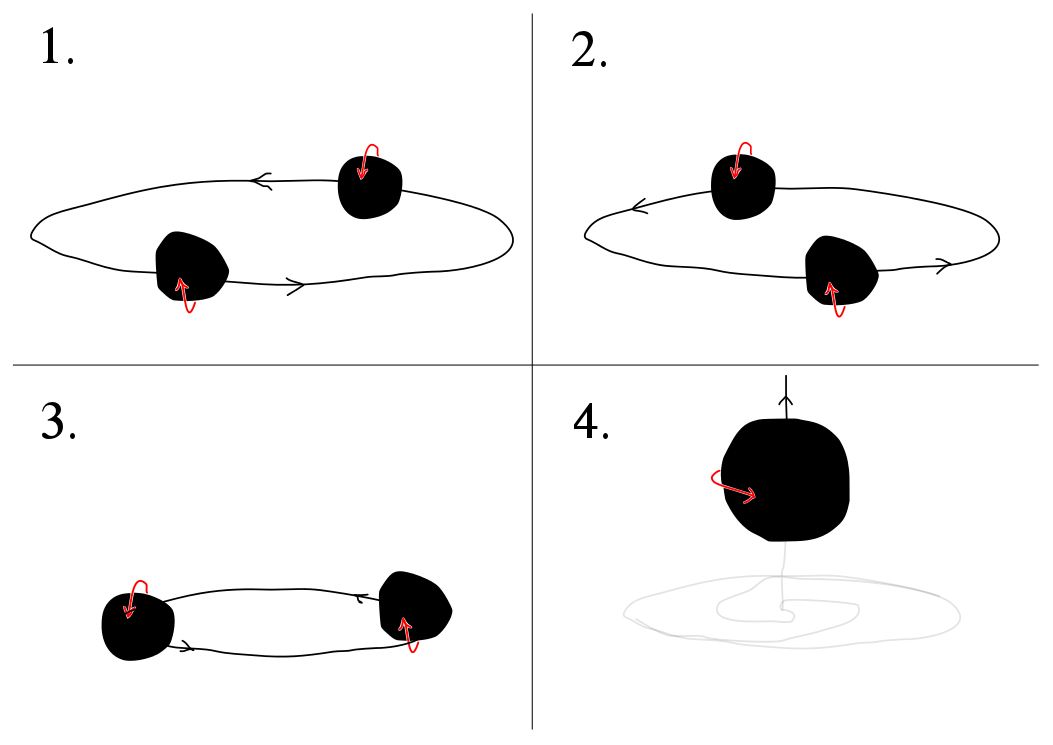
Two black holes orbit, merge, and recoil in a superkick configuration. The four panels show the evolution of the system over time. The red arrows indicate the spin of each black hole, the black arrows represent the black holes’ momenta. Until the very end of the merger, the orientation of the spins is fixed in space: the spins do not rotate with the orbit. Notice in the last panel how the merged hole kicks upward, out of the original orbital plane.
Campanelli et al. suggested this configuration for future study, made an analytic estimate of the maximum kick in the configuration (~1300 km/s) and published their results to the arXiv. A week later Gonzalez et al. published a relativistic simulation of the configuration proposed in Campanelli et al. They extrapolated maximum kick velocities of ~2500 km/s. Within the month Campanelli et al. published further results and extrapolated a maximum kick velocity of ~4000 km/s, directly out of the plane of the orbit.
Why did these groups extrapolate? What parameter were they extrapolating into, and why couldn’t they just simulate the case they thought would yield the largest kick? The mystery parameter was spin magnitude. Kidder’s formulae revealed unsurprisingly that kicks would be largest for maximally-spinning black holes. At the time, no one could simulate a spin of more than 80% of the maximum value. Such a black hole had less than half of the total rotational energy of a maximally spinning black hole. And so these groups had to extrapolate their kick velocities to the extreme limit of spin.
How does this work? Like the ice skater’s fists, the black holes orbit in the x-y plane. Through half of the orbit, their spins beam gravitational radiation preferentially in the -z direction, they recoil up. Through the other half of the orbit, their spins beam preferentially in the +z direction, they recoil down. This spin-orbit coupling increases as their orbits decay and the bobbing motion grows more and more powerful. If the final coalescence occurs during one of these bobs, the merged black hole continues flying off along the z-axis with that final speed. See the figure below for an example of a superkick trajectory.
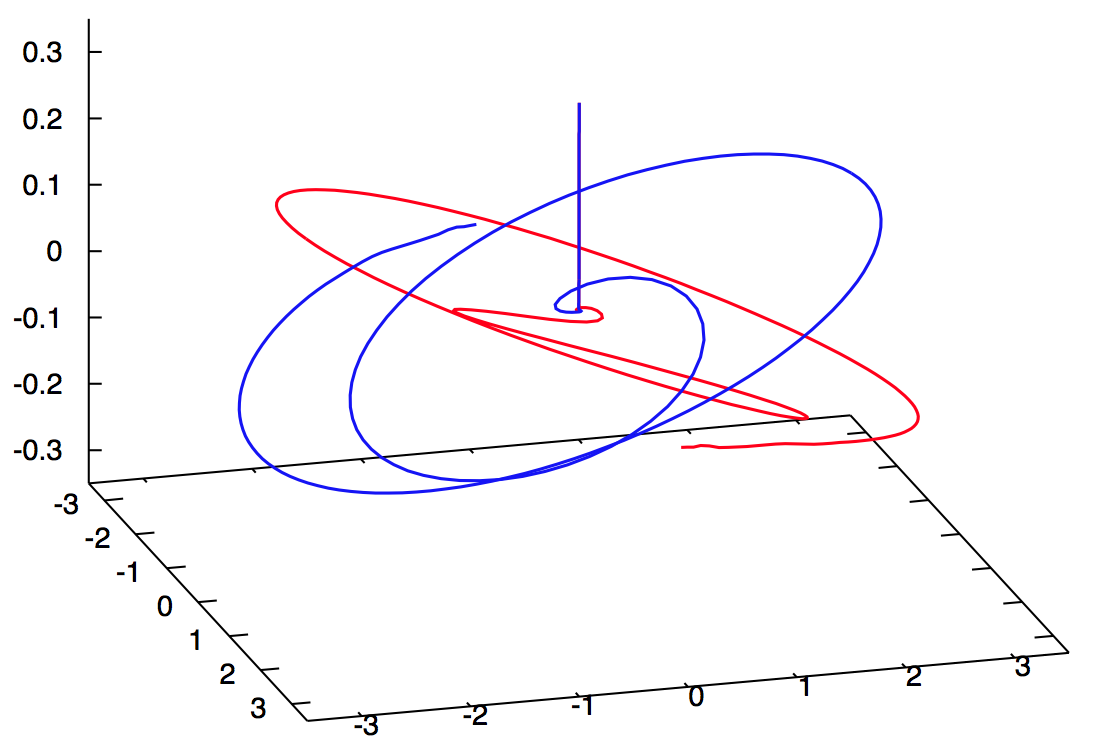
Fig. 4 from Campanelli et al.’s follow-up paper. This shows the trajectories of the two black holes just before they merge. You can see that they move down, up, down,… together along the z-axis. The final trajectory of the merged hole is straight up.
Now we know that even higher kick velocities (15,000 km/s) are possible for very eccentric mergers, but astrophysically-likely mergers will not yield kicks of more than ~3000 km/s (see Sperhake 2010 for both of these statements). Nevertheless these huge velocities are certainly interesting. Galaxy mergers lead to mergers of their central supermassive black holes. Kicks like these exceed the escape velocity of most galaxies (100–1000 km/s). But even if a kick didn’t free a supermassive black hole, it could displace it significantly from the center of its host. Studies are underway to find evidence of such a merger.
By the way, the version-trail of these three papers is a fun case-study in competitive dialogs on the arXiv. In my history above, I read the first versions of the papers to try to understand the development of the idea. But of course, the last versions are even better. Some of the changes indicate they were reading each other (as good scientists should), and some of the changes hint at some competitive tensions. What do you think? Are these types of dialogs fruitful?