Title: “The Kepler dichotomy among the M dwarfs: half of systems contain five or more coplanar planets”
Authors: Sarah Ballard & John Johnson
First author’s institution: University of Washington
Status: Submitted to ApJ

The Kepler dichotomy

The Kepler spacecraft hasn’t just found transiting exoplanets: it’s found transiting exoplanet systems. Hundreds of alternative Solar-systems have been spotted just a few hundred light years away, and Ballard & Johnson want to use them to describe the population of planetary systems across the entire galaxy.

Exoplanets only transit if they pass between their host star and the Earth, blocking out a little light once every orbital period. Sometimes we see more than one planet transit in the same system, which means they lie in the same plane and have small ‘mutual inclinations’ (the angles between exoplanet orbits within a planetary system). But how can you be sure that you detect all the planets in a system? If planets always orbited their stars in a single plane, with very small mutual inclinations, you’d see them all transit. But we know (through radial velocity measurements that reveal additional non-transiting planets in the systems, and through planets passing in front of star-spots, or in front of other planets) that planetary systems are often not well aligned and sometimes have large mutual inclinations.

Although Kepler has found lots of multiple planet systems (multis), it has also found lots of single planets (singletons – that’s what Ballard & Johnson call them). I mean LOTS of singletons. Is this large number of singletons what you would expect to see, given some distribution of modest mutual inclinations? Can the single population be explained by assuming that they have non-transiting friends? Or is there some mysterious process generating all these singletons?

This mystery has been investigated previously for Sun-like stars (Morton & Winn, 2014), where evidence was found for separate populations of singletons and multis. Ballard & Johnson apply the same logic to the M dwarfs, the small stars, to see whether the same dual population phenomenon exists in the mini-planetary systems.

The planet machine

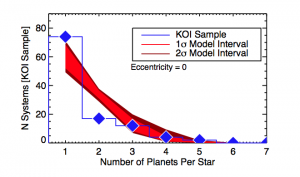
Figure 1. The model is shown in red with its 1 and 2 intervals. The blue histogram represents the observations. Ballard & Johnson find that they cannot adequately reproduce the observations with a single population of planets.

Ballard & Johnson compare the exoplanets observed by Kepler to a fake set of planets. They generate thousands of M dwarf planetary systems with between 1 and 8 planets and mutual inclination scatter ranging from 0-10^o. They then actually tested whether their fake planetary systems were stable and got rid of any that would shake themselves apart through planet-planet interactions. For each system they recorded the number of planets that would be seen to transit and created a histogram of the number of transiting planets. This histogram was parameterised by N (the total number of planets per star) and (the scatter in mutual inclinations of the planets). They then determined which values of N and best describe the observations by comparing their fake-data histogram to the real-data histogram using a Poissonian likelihood function.

Two populations of planets . . .

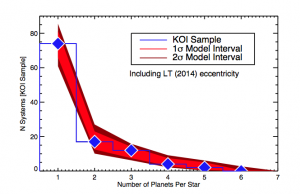
Figure 2. The same as Figure 1 but this time two planet populations are used: one with 1 planet only and one with 2-8 planets.

Ballard & Johnson found that they couldn’t reproduce the observations with this simple model: they couldn’t create enough singletons to match the observations. This is shown in Figure 1 (above)—see how the model (in red) just can’t quite get up to the same height as the observations (the blue histogram) for the singletons.

Next, the authors tried generating two populations of planets: one of singletons only, and another with 2-8 planets and a range of mutual inclination scatters. The ratio of number-of-singletons to number-of-multis, f, was an additional parameter of their model. Ballard & Johnson generated thousands of planetary systems with varying numbers of planets, mutual inclinations and fs. Once again, they counted how many would transit and made a histogram, then found the values of N, and f that best reproduced the data. This time they were able to reproduce the observations—see Figure 2. The sharp upturn in the number of singletons seen in the observations (the blue histogram) is matched by the model (in red). They find a value of f that best reproduces the data: 0.55 ^+0.23_-0.12, so around half of the systems are multis and half are singletons. For the multis, they find that there must be more than five planets per planet–hosting star, with small mutual inclinations, in order to reproduce the observations.

Trending hosts?

Having found that two populations of planets, one of singles and one of multis, best describe the data, Ballard & Johnson ask: is there a fundamental difference between the singleton hosts and the multi hosts? They looked at the host stars’ rotation periods, metallicities (the amount of heavier elements like Helium, Carbon, etc, in the star) and positions in the galaxy and found that the multi-hosting stars tend to be rotating more rapidly, are more metal poor and are closer to the galaxy’s midplane. The rotation trend might actually be an age trend: old stars spin slower than young stars, so perhaps we’re seeing that young systems have lots of planets that get shed over time. These findings are consistent with previous studies.

In this paper, Ballard & Johnson show that with some smooth statistical moves, you can probe an underlying population of objects even though you only observe a fraction of them. They show that the Kepler dichotomy persists for the mini Solar systems—intensifying the mystery behind the singleton excess. Some process that we don’t yet understand is generating all these singletons…. turns out it’s a lonely existence for most exoplanets.