Authors: G. R. Davies, W. J. Chaplin et al.
Title: Asteroseismic inference on rotation, gyrochronology and planetary system dynamics of 16 Cygni
First author’s institution: Laboratoire AIM Paris-Saclay, CEA/DSM – CNRS – Univ. Paris Diderot – IRFU/SAp,
Status: Accepted for publication in MNRAS
Black swan, white swan
16 Cyg A and B are twin stars that revolve around their common centre of mass in the constellation of Cygnus, ‘The Swan’. They are not just twinned with each other by gravitational attraction, they are also extremely alike in mass and age. These stars are similar to the Sun in mass and age, so provide great test-beds for Solar physics. But despite being two of the best studied stars in the galaxy, their rotation periods (the rate at which each star spins on its axis) have remained elusive. Enter asteroseismology.
One of the reasons why asteroseismology is so awesome.
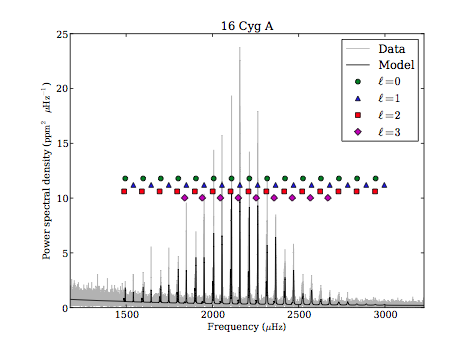
Figure 1. The Fourier transform of the Kepler photometry of 16 Cyg A. The comb-like structure shows the oscillation modes. The data are in grey, the model is in black and the coloured shapes show the positions of the main oscillation modes, indexed by different ‘l’ values. The Fourier transform for 16 Cyg B looks very similar to this.
Asteroseismology was the tool used by Davies et al. to measure the rotation periods of 16 Cyg A and B. Here’s a little background on asteroseismology…
Stars oscillate, or ‘pulsate’ if you like, in a range of ways. Some stars oscillate like the Sun (and are unsurprisingly called ‘Solar-like oscillators’), with p-mode oscillations which produce repetitive fluctuations in brightness. The ‘p’ stands for ‘pressure’ because these oscillations are produced by periodic pressure variations in the convective envelopes of stars. Stars oscillate at a set of discrete frequencies, these are the oscillation ‘modes’. Each mode describes a different wave across the surface or through the interior of the star and therefore takes a slightly different path to all the other modes. The unique frequency of each mode is related to the integrated sound speed along its path and so measuring mode frequencies reveals the internal structure of the star.
Asteroseismologists measure the internal structures of stars observed by the Kepler spacecraft by producing Fourier transforms of the photometric Kepler data, just like the one in Figure 1. The modes appear as a series of peaks, producing a ‘comb-like’ structure.
What about rotation?
The rotation of a star causes splitting of the modes, i.e., instead of single peaks, double peaks appear in the Fourier transform with a small separation, . This occurs because rotation lifts the degeneracy between certain oscillation modes. In a non, or slowly rotating star, the frequency of a pressure wave travelling across its surface doesn’t depend on latitude. Adding a little rotation causes the star to bulge at the equator and, all of a sudden, latitude does matter. Waves travelling across the stellar surface at the poles have a slightly different frequency to those at the equator. This difference is greater for faster rotators. For more details see Chaplin et al. (2013). The amount of splitting, i.e. the magnitude of
, depends on both the rotational velocity and the inclination angle of the star: a star viewed from above will not show the same amount of mode splitting as a star viewed equator-on.
Davies et al. used the observed frequency splitting to infer the inclinations and rotation periods of 16 Cyg A and B, finding that A has a rotation period of around 24 days and B has a rotation period of 20-30 days.
What’s the big deal?
One of the easiest ways to measure rotation with Kepler data is to look for variations in brightness caused by star spots on the stellar surface. These spots reduce the overall brightness of the star whenever they appear on the side facing us, once every rotation period. By measuring the intervals between periodic dips produced by star spots it is often possible to measure surface rotation. Unfortunately, 16 Cyg A and B are ‘quiet’ stars: they don’t have very many star spots, so this method wasn’t available. Asteroseismology produces the best measurements of the rotation periods of these stars.
Testing age-rotation relations
Stars like the Sun are expected to shed angular momentum over time and slowly spin down as they get older. The rate of rotational braking is the same for stars of similar masses. 16 Cyg A and B have similar masses and are the same age, so you would expect them to have similar rotation periods. The exact relation between age, mass and rotation period isn’t very well understood and still needs some calibrating. These stars will be extremely important for calibrating this relation, improving our ability to measure the ages of main sequence stars from their rotation periods. This paper provides a Cygnificant* contribution to the field of stellar dating.
*Couldn’t help myself.



Trackbacks/Pingbacks