Paper: A Search for short-period Rocky Planets around WDs with the Cosmic Origins Spectrograph (COS)
Authors: P. H. Sandhaus, J. H. Debes, J. Ely, D. C. Hines, M. Bourque
First author’s institution: The Ingenuity Project; Space Telescope Science Institute
Status: Accepted for publication in ApJ

The Hubble Space Telescope. Might it accidentally have found a planet around a white dwarf? Image Credit: NASA
White dwarfs, the tiny, burnt out cores that stars like the Sun leave behind when they run out of fuel, are a surprisingly ideal place to look for potentially habitable planets. As white dwarfs are only about the size of the Earth, even a small planet will block out a large amount of the white dwarf’s light in a transit. An Earth-sized planet, passing in front of the white dwarf, could block nearly all of the light that we pick up from it, compared with the tiny fractions of light blocked when a planet passes in front of a normal star. Such a transit would be very easy to detect.
Additionally, white dwarfs are much dimer than normal stars. For planets to be warm enough to potentially support life, it would have to be extremely close to the star. The closer it is, the less time it would take to go around the white dwarf, so would transit more often, increasing the chances of us spotting a transit.
The flaw in this argument is that before they become white dwarfs, Sun-like stars swell up into huge red giants, destroying any nearby planets. For a planet to be in the white dwarf’s habitable zone, it would have to be scattered in by an encounter with a larger planet after the giant phase. However, this scenario isn’t unreasonable, as astronomers have already found evidence for objects nearing the size of dwarf planets close into white dwarfs. There may well be transiting, potentially habitable planets around white dwarfs, waiting for us to find them.
The authors of today’s paper have checked to see if we haven’t already found one, entirely by accident. To do this, they exploited a unique feature of one of the instruments on the Hubble Space Telescope.
The Cosmic Origins Spectrograph, or COS, was installed on Hubble in 2009, as part of the last Space Shuttle servicing mission. COS is an ultraviolet spectrograph, splitting the light from the objects it looks at to explore the signatures left by different chemicals. As ultraviolet light is blocked by the Earth’s atmosphere, this kind of science can only be done in space.
Sandhaus et al. use two features of COS to search for planets around white dwarfs. Firstly, white dwarfs are often at their brightest when viewed in ultraviolet light, and tend not to change much over time. This makes them excellent calibration targets for COS: if a selection of white dwarfs are observed every so often, any changes in the result are most likely due to the instrument, not the white dwarf. Over COS’ lifetime, the authors found that the total length of time spent observing seven white dwarfs has become long enough to begin searching for planets.
But these observations were spectra, not the light curves needed to check for transits. Most spectrographs use a CCD detector, where the light from the star builds up for a set exposure time, before being read out all at once. This makes it impossible to know how, or if, the brightness of the target changed over the course of the exposure.
However, COS’ detectors use slightly different detectors, where the pixels of a CCD are replaced by devices similar to photo-multiplier tubes. Each photon hitting the detector can be individually recorded. Sandhaus et al. used this feature to recored exactly how much light was hitting the detector at any given time, with a time-resolution of just 15 seconds.
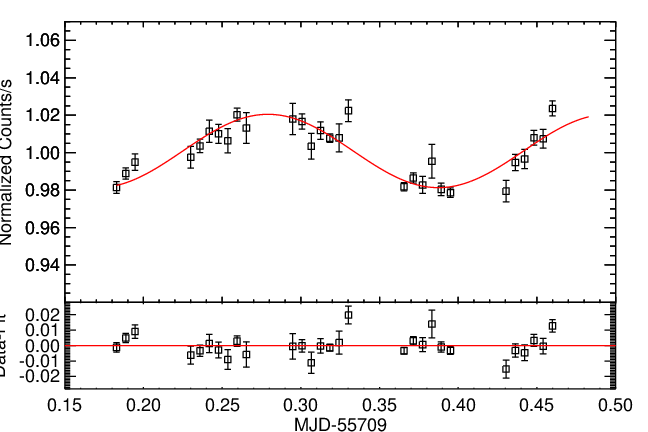
Light curve of the white dwarf GD 133, extracted from COS data. The y-axis shows the light from the white dwarf over time, normalised so that the average=1. The x-axis shows the time that the observations were obtained. Although the authors didn’t spot a planet, the light curve shows that GD 133 appears to pulse on a 5.2 hour period.
Unfortunately, the authors didn’t find any planets around any of the seven white dwarfs. However, they could use this non-detection to explore COS’ potential for spotting white dwarf planets in the future. This was done by adding some fake transits into the light curves, which mimicked the loss of light caused by objects of various sizes. The size of the pretend object was then increased until the transit could be spotted in the data. Sandhaus et al. found that, even at the very faintest white dwarfs, objects as small as Pluto or even Ceres could be spotted.
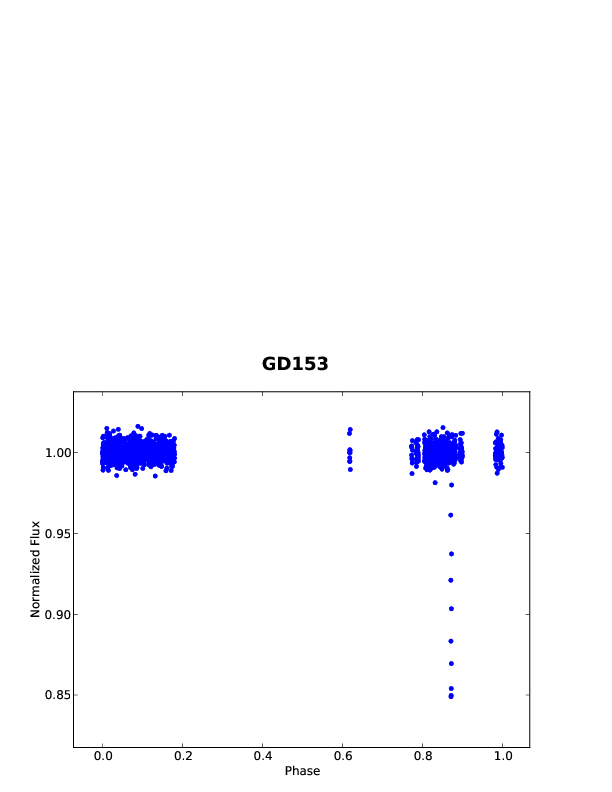
Light curve of GD 153, with a transit of a 0.5 Earth radius planet added in. The transit is clearly visible, blocking out 15% of the light, much more than it would at a normal star.
The authors finish by pointing out that, as well as getting a free light curve, you’re still getting a spectrum! If a planet were to be discovered around a white dwarf in the future, the small size difference could make for very effective transit spectroscopy. The ultraviolet range is a good place to look for oxygen, and it could be years until similar observations are possible at other stars. Future COS observations of white dwarfs* could be a key tool in the search for Earth-like planets around white dwarfs.
*In the interests of full disclosure, I should point out that this astrobiter’s PhD relies on COS observations of white dwarfs, so may be slightly biased in calling for more of them!