Title: The Most Massive Galaxies and Black Holes Allowed by ΛCDM
Authors: Peter Behroozi, Joseph Silk
First Author’s Institution: Department of Astronomy, University of California at Berkeley
What is the most massive possible galaxy in the observable universe at a given time? That’s the question today’s paper seeks to answer, and it does so by combining assumptions from our current model of the universe with our knowledge of how galaxies form and evolve throughout cosmic history.
We have a standard cosmological model of the universe, the Lambda Cold Dark Matter model (ΛCDM), that does a pretty good job of explaining a number of properties of the universe that we observe. One of the fundamental properties of this model is that it tells us the ratio of dark matter to ‘normal’ matter — the stuff you and I are made of. Astrophysicists call this familiar stuff baryonic matter. Dark matter has never been seen explicitly, but its presence is inferred from its gravitational effects on large scales. The most recent estimates from the Planck satellite put the fraction of baryonic matter to dark matter, fb, at around 0.16 – there is far more dark matter than baryonic matter in the universe, a surprising fact considering we have hardly any idea what dark matter actually is.
In ΛCDM dark matter typically arranges itself over time into ‘halos’, immense, quasi-spherical structures that create huge gravity wells. These halos are the birthplaces of galaxies: they are the sites where baryons fall in, coalesce and form galaxies. As such, there is expected to be a very close relationship between the properties of a galaxy and the properties of its host halo.
The ratio of baryons to dark matter places a limit on the size of a galaxy that can form in a dark matter halo – you can’t form a galaxy with more baryons than there are in your environment. In addition, massive stars and black holes can blow away precious gas, further limiting the amount of baryons that are able to fall into a dark matter halo.
We can’t actually observe dark matter halos, but we do observe galaxies. We can therefore turn this ratio around and estimate the size of the dark matter halo given the size of the galaxy. So, for a galaxy with size M* the host halo must must have a mass MH greater than M*/fb. For a baryon fraction of 0.16 this gives MH > 6.3 M*. When we include the effect of stars and black holes blowing away gas, this can limit the amount of baryons falling into the halo by up to 30%: if we include this in our inequality above we get a minimum halo mass of 21 M*.
ΛCDM can predict the expected number of dark matter halos of a given mass at different times in the universe’s history. The authors of today’s paper argue that if we see a massive galaxy, we can use the inequalities above to estimate its halo mass, and use this to test whether ΛCDM is correct, or at least whether our assumptions about galaxy formation are correct. They provide estimates of the kinds of galaxy masses at different times in the universe’s history that would lead to tension with ΛCDM, or our understanding of baryonic physics (see Figure 1). These estimates change over time as galaxies grow; a galaxy with a particular mass earlier in the universe is less likely to exist than later on, since at later times galaxies have had time to assemble much higher masses.
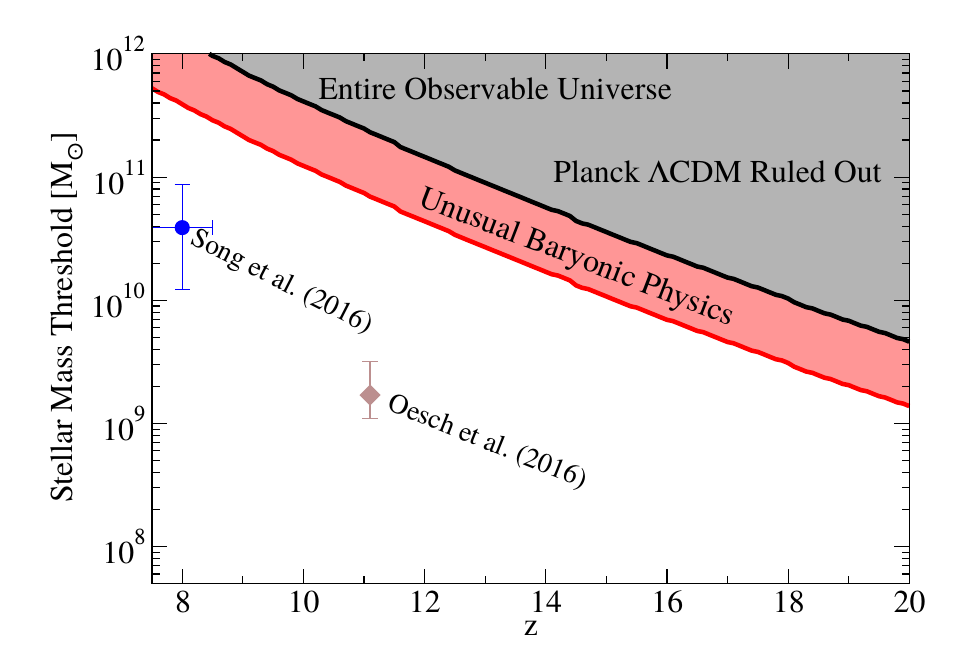
Figure 1: The threshold for the mass of stars in a galaxy against redshift. If a survey of the entire observable universe found that galaxies had stellar masses greater than the black line at a given redshift, it would rule out ΛCDM as a viable cosmological model. If masses greater than the red line were observed it would require a rethink of how stellar feedback works in galaxies. Some of the latest observational results are plotted, showing that ΛCDM is currently still fit to fight another day.
A similar procedure can be used with black hole masses. Supermassive black holes appear to lie at the heart of every galaxy, and can be seen far back into the universe’s history. We can get rough estimates of their masses, and then infer their galaxy masses using a theoretical ratio of the black hole mass to the galaxy mass. Given this, we can then infer the mass of the halos that host them using the ratios above. Figure 2 shows the limits for such an estimate, against recent observations of high redshift quasars (active supermassive black holes).
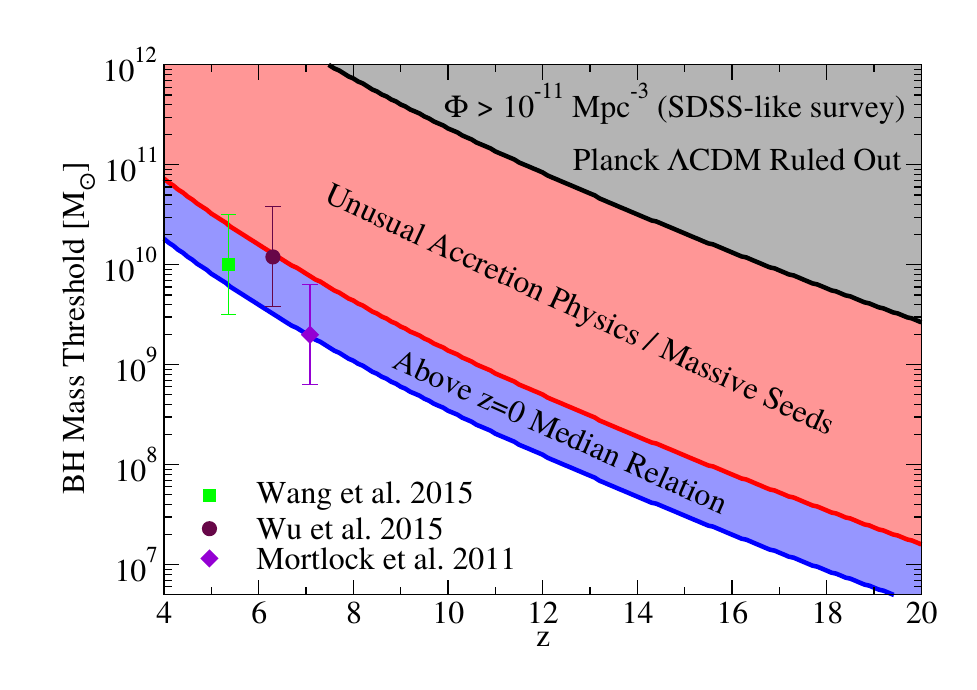
Figure 2: Threshold black hole masses against redshift for a survey similar to the Sloan Digital Sky Survey (SDSS). For black holes above the red line, new physics of galaxy formation would have to be invoked, or black holes would have to be birthed by massive seeds in the very early universe. Above the blue line, the ratio between black hole mass and stellar mass is greater than in the local universe. Many recent observations seem to suggest this is the case.
All of these estimates are riddled with assumptions, which the authors are up-front about. For a start, it’s difficult to estimate the mass of a galaxy just from its luminosity. This has a knock-on effect on the estimate of the ratio of the black hole mass to the galaxy mass. The redshift of galaxies and black holes is also often uncertain. The authors also highlight the Eddington Bias, a statistical effect explained well here, that could affect the observed number densities of galaxies and black holes.
Despite these uncertainties, the method shown here provides a neat way of testing cosmological models, as well as our understanding of stellar and black hole feedback. Upcoming surveys, from space-based observatories such as the James Webb Space Telescope (JWST) and the Wide-Field Infrared Survey Telescope (WFIRST), will probe further back into the universe’s history, and may spy massive galaxies that don’t fit our current models of the universe. Giant galaxies are exciting anyway, but when they can potentially rubbish our ideas of how the universe works they become even more compelling objects to hunt down.