Title: The effect of superfluid hydrodynamics on pulsar glitch sizes and waiting times
Authors: B. Haskell
First Author’s Institution: The University of Melbourne, Australia
Status: Monthly Notices of the Royal Astronomical Society: Letters, open access
Rotating neutron stars (pulsars) can “spin-up”, or suddenly increase their rotation frequency, in an event called a glitch (see Figure 2 for a canonical example of a pulsar glitch). There is a scarcity of glitch observations, meaning that drawing statistical conclusions must be done with caution! Nevertheless, some of the observed properties of glitches are quite curious. In general, the distributions of observed glitch sizes are a power law (which would be consistent with the microscopic mechanisms believed to cause the glitches). However, the Vela pulsar, for example, typically has large glitches which occur fairly periodically, while recent analysis of the Crab pulsar indicates there is a deviation from a power law distribution for smaller glitch sizes. This paper tackles this discrepancy by showing that these deviations from power law distributions can be explained naturally, using a carefully chosen model that bridges microscopic and macroscopic scales.
What is a pulsar?
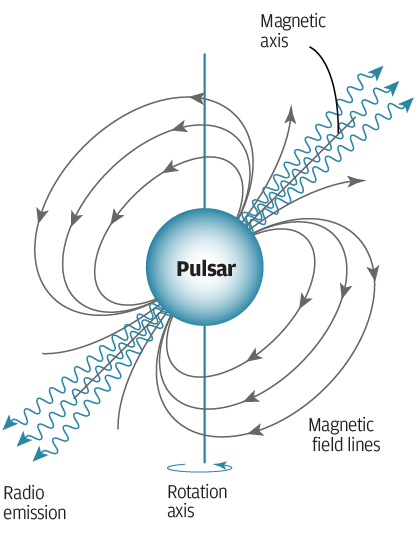
Figure 1: The misalignment of the magnetic and rotation axes of a pulsar leads to electromagnetic emission we see as periodic “pulses” on Earth. Image source: http://www.scmp.com/infographics/article/1974448/interactive-everything-you-need-know-about-chinas-giant-new-radio
A pulsar is a rotating neutron star that emits beams of electromagnetic radiation (see Figure 1). These beams sweep over the Earth much like a lighthouse projects a rotating light beam out to sea. Certain millisecond pulsars radiate pulsed emission with a regularity rivaling even an atomic clock! The periods of rotation of pulsars can be used for a whole range of different applications. Pulsars orbiting in the strongly curved spacetime around supermassive black holes can potentially be used to probe strong gravitational fields, as the distorted paths travelled by the electromagnetic waves affect the arrival times of the pulses on earth. Pulsar Timing Arrays can be used to measure the disruption of spacetime due to passing gravitational waves and this was how the existence of gravitational waves was first indirectly confirmed (by measurements of the Hulse-Taylor pulsar).
A neutron star has more than the mass of the Sun contained in a sphere the size of a small city. So, as you can imagine, there are considerable gravitational forces and extremely high nuclear densities at play here. In many respects, a neutron star is like a giant atomic nucleus and contains some of the densest matter in the Universe. Consequently, pulsars have some surprising and unique properties.
Glitches: astronomical anomalies
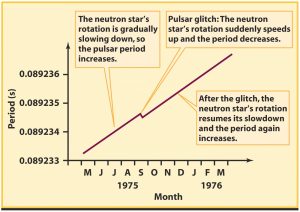
Figure 2: Anatomy of a pulsar glitch. Occasionally, the opposite behaviour (i.e. a rapid slow down in rotation frequency) can be observed in an “anti-glitch”! See bites 1 and 2 for more information about this. Image source: https://briankoberlein.com/2014/05/30/glitch-anti-glitch/.
As mentioned before, the rotation of certain pulsars is incredibly stable. Nonetheless, pulsars can exhibit some quite weird behaviour as they rotate – for example, the mechanism underlying glitches in pulsar rotation frequency is still not fully understood, forty years after they were first observed! However, glitches are likely to be associated with a property called superfluidity which is exhibited by the material inside a neutron star.
Theoretical calculations show that neutrons in the interior of a neutron star are likely to form a superfluid, which is a substance that flows without friction. There is observational evidence for this property as well (for example the cooling of Cassiopeia A). Superfluidity has a dramatic impact on the rotational dynamics of the star, as a rotating superfluid (such as superfluid Helium or an atomic BEC) forms quantised vortices above a critical angular velocity. Each of these vortices carries a single unit (or “quantum”) of circulation and their configuration entirely describes the rotation of the neutron fluid. As the star spins down, vortices are naturally expelled from the superfluid (by moving radially outwards and “annihilating” at the edge). However, vortices can “pin” to ions in the crust, meaning that some vortices get stuck in one spot! This means the superfluid interior cannot imitate the smooth spin down of the neutron star crust and the angular velocity lag that builds up is corrected by the sudden spin-up events that we call glitches, as vortices unpin from the crust. This explanation successfully describes many features of pulsar glitches.
Vortex Avalanches
But, we still do not know exactly how such a vortex unpinning event is triggered in the star! One possible mechanism is where the built up stress is relieved by sudden “vortex avalanches” (i.e. self-organised critical behaviour where the system self-regulates the buildup of stress with local avalanches of vortices unpinning at the same time). If self-organised criticality underlies the physics of the unpinning trigger, then the distribution of the avalanche sizes will be a power law. This paper assumes that vortex avalanches are indeed the cause of glitches but the author notes that there are other possible scenarios such as starquakes and superfluid instabilities.
Results
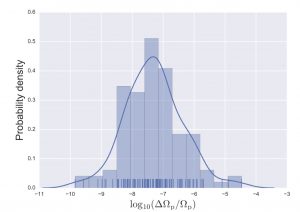
Figure 3: Probability distribution function for glitch sizes (). The distribution deviates substantially from a power law for smaller glitch sizes. Figure 1 in paper.
This paper attempts to explain the observed discrepancies from a power law distribution of glitch sizes, by taking a macroscopic hydrodynamical superfluid model and inputting results from microscopic quantum mechanical simulations of vortex avalanches. Essentially, large-scale hydrodynamics gives rise to deviations from power law glitch size distributions – even though vortex avalanche sizes (at the micro scale) are still power law distributed. According to the simulations in this paper, very small changes in the spin down rate are gradual rather than sudden, and therefore do not get counted as glitches. This means there is a “cut-off” in the distribution – an absence of smaller glitches – as seen in Figure 3.
By incorporating the effect of large scale hydrodynamics on microscopic vortex avalanche models, the author of this paper has found a possible solution to the observed deviation from power law in glitch size distributions.

Trackbacks/Pingbacks