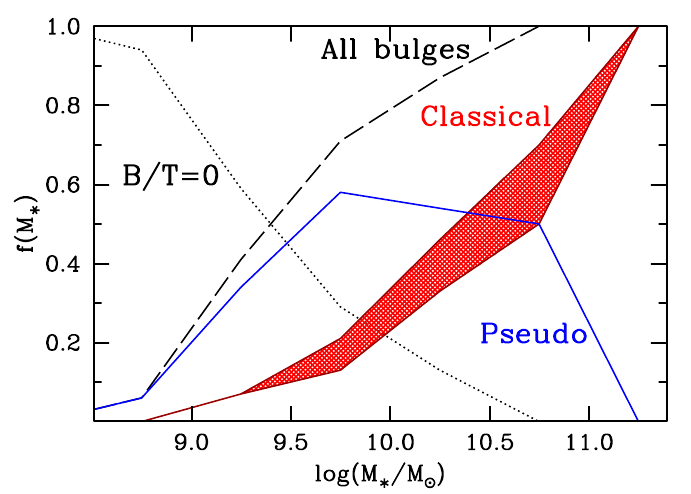
Title: Spin-up of massive classical bulges during secular evolution
Authors: Kanak Saha, Ortwin Gerhard, and Inma Martinez-Valpuesta
First Author’s Institution: Inter-University Center for Astronomy and Astrophysics, Pune
Status: Accepted for publication in Astronomy & Astrophysics, open access
Sandeep Kumar Kataria is a 3rd year PhD student at the Indian Institute of Astrophysics as a part of the Joint Astronomy Program of the Indian Institute of Science, Bangalore. His research interests lie in galactic dynamics and galaxy evolution. His hobbies are running, cycling, and playing volleyball. Apart from this, in his free time he likes to do science outreach in schools and play flute.
Introduction:
The mass of spiral galaxies is mainly distributed in three components: the classical bulge (ClB), disc, and surrounding dark matter halo. Classical bulges are the central building blocks of many early-type spiral galaxies (see the Astrobites Guide to Galaxy Types). These bulges might have formed as a result of collisions between galaxies in the early universe or various other processes mentioned in this paper. It is believed that initially the motion of stars in ClBs is disordered, so the ClB does not rotate. The authors of this paper see an interesting problem to ponder: in the present day, there is an observed net rotation of stars in classical bulges. The origin of this rotation is still to be understood in detail.
One of the authors of this paper has explained in earlier work that low-mass classical bulges spin up by absorbing angular momentum from galactic bars. The bar has a pattern speed, which is a measure of the collective rotation of a family of orbits of stars in the bar. Angular momentum exchange from the bar mainly occurs at resonances in the disc. These are locations where the difference between disc’s rotation speed and the bar pattern speed have specific ratios with radial oscillations of the stars in the disc. These resonances can be thought of as analogous to resonances in an organ pipe, the natural frequency of which corresponds to waves with wavelengths which match the length of the organ pipe. Let’s see how the authors approach the solution of the rotation problem in ClBs.
Experiments with galaxy models using computers:
The authors of this paper try to explain net rotations in Massive ClBs using N-Body simulations. First, models of galaxies having non-rotating classical bulges of different
masses and sizes are generated using well known techniques such that these models are not unstable. One of the well known classical parameters of local stability is the Toomre Parameter. This parameter measures the ratio between inward gravitational pull on stars at a particular point, and the radial motions of stars at that point. If these motions are sufficiently strong, the gravitational pull will be insufficient to overcome them and the disc will be locally stable. All the models, after evolution, form bars of different sizes according to the initial value of the Toomre parameter. Further, the point of interest lies in understanding how these bars transfer angular momentum to ClBs.
Studying Bulge Kinematics from experiments:
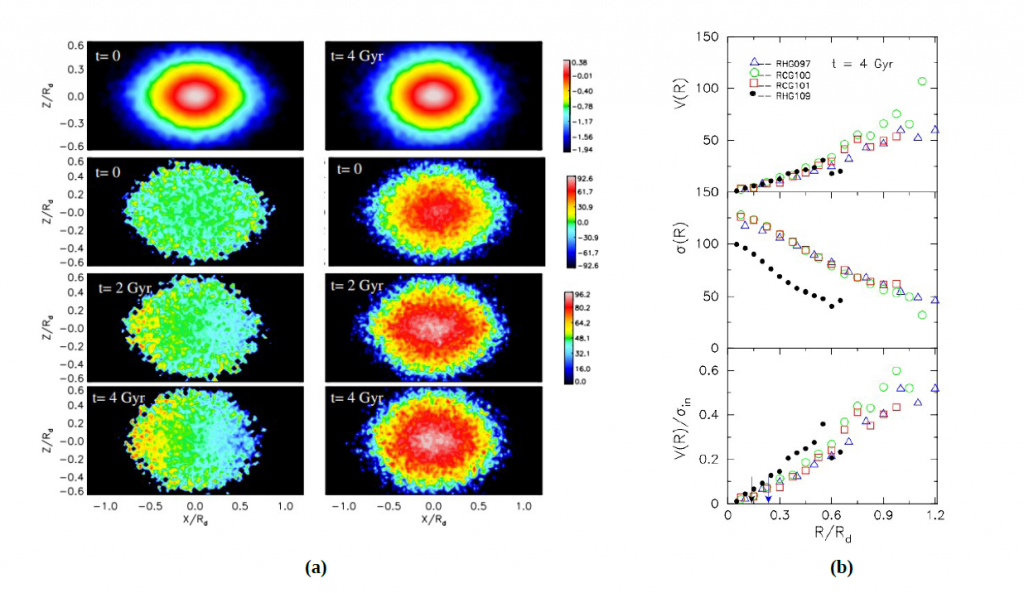
Figure 1a. Top row – surface density maps of the model with the highest mass ClB at different times during its evolution. Second to fourth rows – line-of-sight velocity (left) and velocity dispersion (right) maps at different times. These images are taken at 90° projection (edge-on view) and the major axis of the bar is aligned with the x-axis. Clear signatures of rotation are seen at 4 Gyr. The colour bar at the top represents density, middle the velocity, and bottom the velocity dispersion.
Figure 1b. Rotation, velocity dispersion, and local V/σ radial profiles for the four ClBs in the models.
The authors notice changes in orbital configuration due to angular momentum transfer by the bar. From Figure 1a it can be noticed that the rotational component in the outer part of the bulge increases over time. It can also be seen that the central part of bulge becomes ‘hot’ and slightly rounder. Here ‘hot’ means that orbits of stars become more disordered and their velocity dispersion (σ) increases. Figure 1b shows radial profiles of rotation and dispersion of stars in the bulge at 4 Gyr for a few of the simulated models. It can be deduced that ClBs rotate faster in their outer parts. However, comparing simulated rotation data of ClBs with observations is no easy task: observational rotation data contains stars both in bulges and bars and distinguishing which they belong to at a single moment in time is challenging.
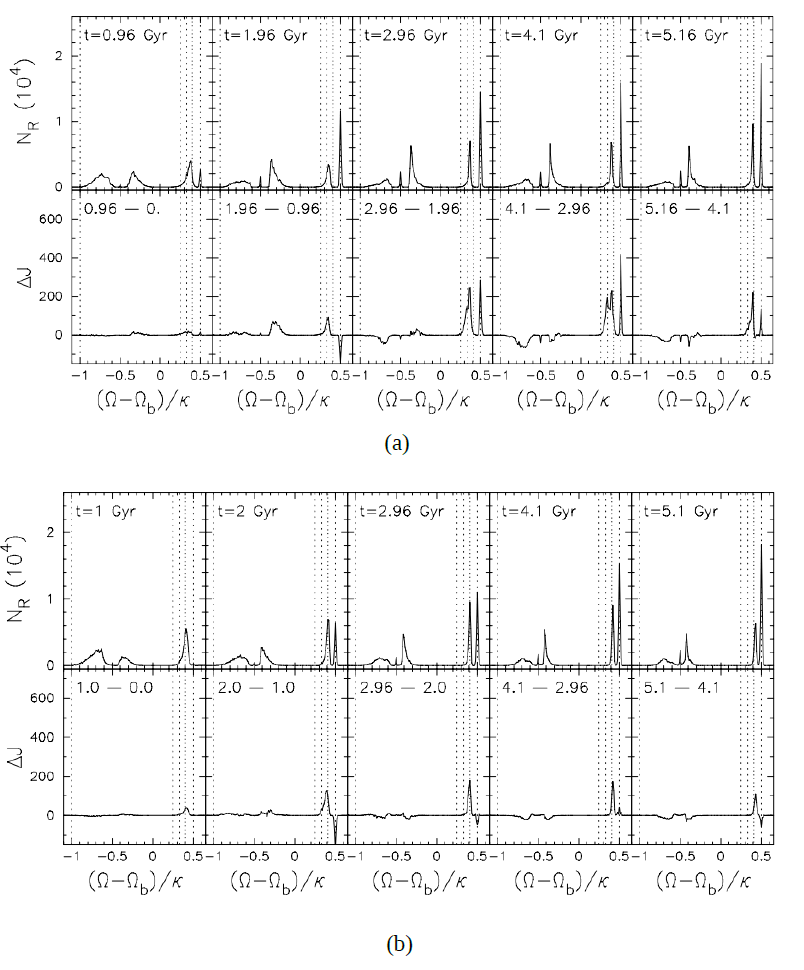
Figure 2a. Top row: distribution of bulge stars with frequency (Ω − ΩB)/κ at different times throughout the secular evolution in the model with the lowest bulge mass. Bottom row: net change in the angular momentum of the selected stars with respect to the previous time. The vertical dotted lines indicate the most important resonances (from left to right): −1:1, 4:1, 3:1, 5:2, and 2:1. As time progresses, more stars are trapped by the 2:1 resonance of the bar with the stellar disc. However, most of the angular momentum transfer occurs through the 5:2 resonance.
Figure 2b. Here the top and bottom rows represent same entities as in the previous figure but for the models with the highest mass ClBs. As with the low mass Classical bulges most of the angular momentum transfer occurs via the 5:2 resonance.
The Spin-up process in Massive Classical Bulges:
After simulating galaxy models with various types of ClBs, the authors conclude that specific angular momentum (angular momentum per unit mass) transfer by the bar is the same for ClBs with low and high mass. Most of the angular momentum transfer from the disc to the bulge occur at particular locations (resonances) which are shown in Figures 2a and 2b. This phenomenon lead to density wakes (alignments of stars in the bulge with the bar) in the bulge. In the simulations density wakes are not so aligned with the bar in the low-mass ClBs but are completely aligned with the high mass ClBs by the end of simulation. The authors also find that outer parts of the bulge experience significant amount of rotation. In addition, the orbits in low-mass bulges are well-ordered, but the ones in high-mass bulges are more disordered. At the end of the simulation all models have a bar with a ‘box’ shape, suggesting that composite bulges (ClB + Boxy Bar) should be common in galaxies. Finally the authors conclude that massive ClBs, like low mass ClBs, are affected by angular momentum exchange with the bar. The spin up process is more prominent when the bar is larger than the ClB.