Title: Where are LIGO’s Big Black Holes?
Authors: M. Fishbach & D. E. Holz
First Author’s Institution: Department of Astronomy and Astrophysics, University of Chicago, Chicago, IL
Status: Posted on ArXiv, 25 Sept. 2017 [open access]
As our readers likely know, the LIGO Scientific Collaboration made history in September 2015 with the first direct detection of gravitational waves. Since the historic initial detection, there have been several more measurements of binary black hole (BBH) mergers (including one announced yesterday!). Today’s astrobite explores a strange question arising from the initial LIGO results: why were the BBH sources much less massive than LIGO’s sensitivity suggests they could be? Though four detections aren’t necessarily representative of an entire BBH population, it turns out that some statistically significant information can still be gleaned from just a few sources.
For its two most recent observing runs, LIGO was technically capable of detecting BBH mergers with individual BH masses up to 100 times the mass of the sun (M); however, the largest component masses measured were only 36 and 29 M
(fortuitously coming from the first detection — GW150914). As it turns out, binaries with one component of at least 40 M
comprise more than 90% of the volume of theoretical detections available to LIGO during that time. How is it possible that we didn’t see any massive BBH coalescence events? The authors of today’s paper (succinctly titled, “Where are LIGO’s Big Black Holes?”) suggest the presence of a gap in the expected distribution of BH masses.
Determining the way in which mass is distributed throughout populations of stars in the Universe is a complex and longstanding astronomical problem. For example, the initial mass function (IMF) has been the subject of countless empirical and theoretical studies since the 1950s (the most famous being Salpeter in 1955). In the age of gravitational wave-based astrophysics, a similarly important measurement is the distribution of BH masses, especially for those in binary systems. As LIGO is capable of deriving component masses of BHs in merging systems, its continued operation is invaluable in determining this mass distribution. Studies of BHs in X-ray binary systems in the pre-LIGO era suggested that a mass gap exists between heavy neutron stars and light BHs (between approximately 3 and 4 M). Similarly, there is a subtle theoretical argument for a BH mass gap due to pulsational pair instability supernovae (ambitious readers will find an overview in Woosley 2017). Massive stars are sometimes rendered unstable when producing electron-positron pairs in their interiors, causing them to lose significant amounts of mass. The associated mass loss prohibits the formation of massive BHs between about 50 and 135 M
. This upper mass gap is the source of the authors’ curiosity, though LIGO could one day be used to study the lower gap as well.
Is it smart to make conclusions with only four data points?
The LIGO scientific team has relied on a reasonably simple power-law model to describe the mass distribution of detected BBH systems (mass distribution m
, where m
is the larger of the two BH masses). While their model assumes that the maximum detectable BH mass is 100 M
, this is actually conservative, as BBHs with total masses of 600 M
could be detected in LIGO data using nonstandard techniques. Assuming a “normal” Salpeter IMF (
= 2.35), the power-law distribution describing the volume to which LIGO could detect a BBH system is in fact flat in BH mass distribution; that is, it is extremely surprising that they have detected only BH masses less than 40 M
.
To determine if it’s remotely likely to see the thus-far detected distribution of BBH masses, the authors of this paper analyze the confirmed LIGO detections (one of the events, LVT151012, is less certain — it has an 87% chance of being legitimate) as well as a simulated series of detections (see Figure 1). They find that it is very statistically improbable to find four BBH systems with masses less than 41 M if there is no mass gap; in fact, it is 99.9% improbable if one assumes that LIGO is sensitive to BBH total masses as high as 200 M
. They additionally conduct a bayesian analysis that suggests just 10 more measurements with mass < 50 M
would be a near-confirmation of the existence of a mass gap. In order to determine how future LIGO data might help constrain limits on both the mass distribution and the lower bound of the mass gap, the authors construct three populations of 40 detections each. In Figure 1, the left and right columns are given Salpeter IMF values of
= 2.35, and the middle has
= 1. The first two columns set the maximum mass at 50 M
and the rightmost column at 40 M
. Overall, that analysis suggests that a sample of only ~40 BBHs could very tightly constrain both the lower bound of an existing mass gap and the index describing the BBH mass distribution.
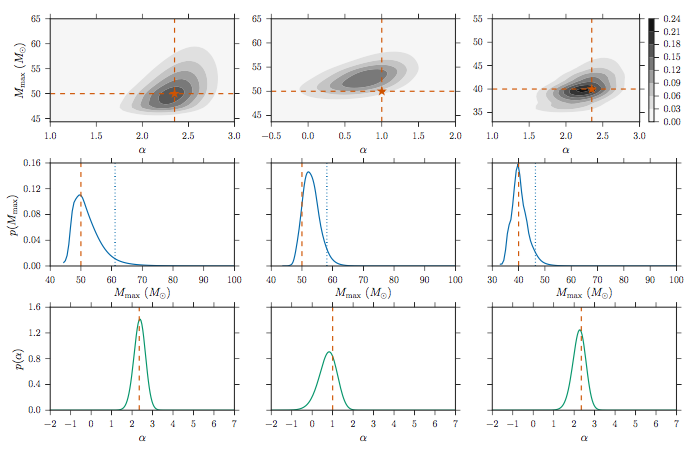
The results of 40 simulated BBH detections. The team shows three populations with different and maximum mass values (maximum mass is the lower bound of the mass gap; that is,
the maximum mass allowed in the lower part of the distribution). Values describing each population are shown with an orange star in the top row. The top row is the recovered probability distribution function for the two parameters, the second row shows the results for maximum mass, and the third for . Figure 5 in the paper.
A gap has two sides, right?
The discussion of a “gap” implies that the distribution of BBH masses continues above the missing area between 50 and 135 M. It’s therefore natural to wonder if LIGO is capable of detecting the higher-mass systems. The instrument, in theory, is several times more sensitive to BBHs with total masses between 270 and 300 M
than it is to systems between 10 and 65 M
(assuming each component BH is of equal mass). It is possible to assume different IMFs in order to determine under what circumstances we would not worry about the non-detection of systems with above-the-gap masses (between 135 and 150 M
). As stated before, a Salpeter IMF implies a power law index
= 2.35. If the IMF index is actually
= 1 (we don’t expect the power law index to apply over the entire range of masses), there are then only 1.76 times more BBH systems with low component masses between 5 and 40 M
than there are systems with masses above the gap. If 10 BBH detections with LIGO yield no above-the-gap mass measurements, it’s safe to conclude that
= 1 is a poor assumption or that there are no BBHs above the gap. Alternatively, assuming a Salpeter
= 2.35 distribution, it would be necessary to detect more than 60 BBHs below the gap to come to any firm conclusions.
The constraints made possible by the detection of only four BBH systems have been impressive; however, many more systems will need to be studied in order to properly probe the BH mass population. LIGO will begin its next observing run, O3, in Fall 2018. The ability to study a set of many measurements from future observing runs will prove invaluable in several astrophysical disciplines, including stellar evolution, supernovae, and compact binary formation. Today’s astrobite suggests that it won’t take an enormous number of LIGO detections to produce immensely useful scientific results, so there’s still work to be done as we wait for O3 to begin.
(Featured image shows the Virgo detector; courtesy Marco Kraar)

Is there a reason we don’t have a direct link to the arxiv.org preprint?
https://arxiv.org/abs/1709.08584
As we used to say in particle physics: “One event is a cross section, two events is an angular distribution.” Milk those 4 events for all they are worth!