Title: The great impostors: Extremely compact, merging binary neutron stars in the mass gap posing as binary black holes
Authors: Antonios Tsokaros, Milton Ruiz, Stuart L. Shapiro, Lunan Sun, Kōji Uryū
First Author’s Institutions: Department of Physics, University of Illinois at Urbana-Champaign, Urbana, USA
Status: Open access on ArXiv
Gravitational wave astronomy is a field brimming with promise, with LIGO–Virgo discovering new clues to a number of scientific mysteries, such as the origin of heavy elements and the progenitors of short gamma-ray bursts. One such mystery is the lack of observed neutron stars or black holes in the ~3 to 5 solar mass range, i.e. the ‘mass gap‘ which shows up as a conspicuously empty band in the schematic below.
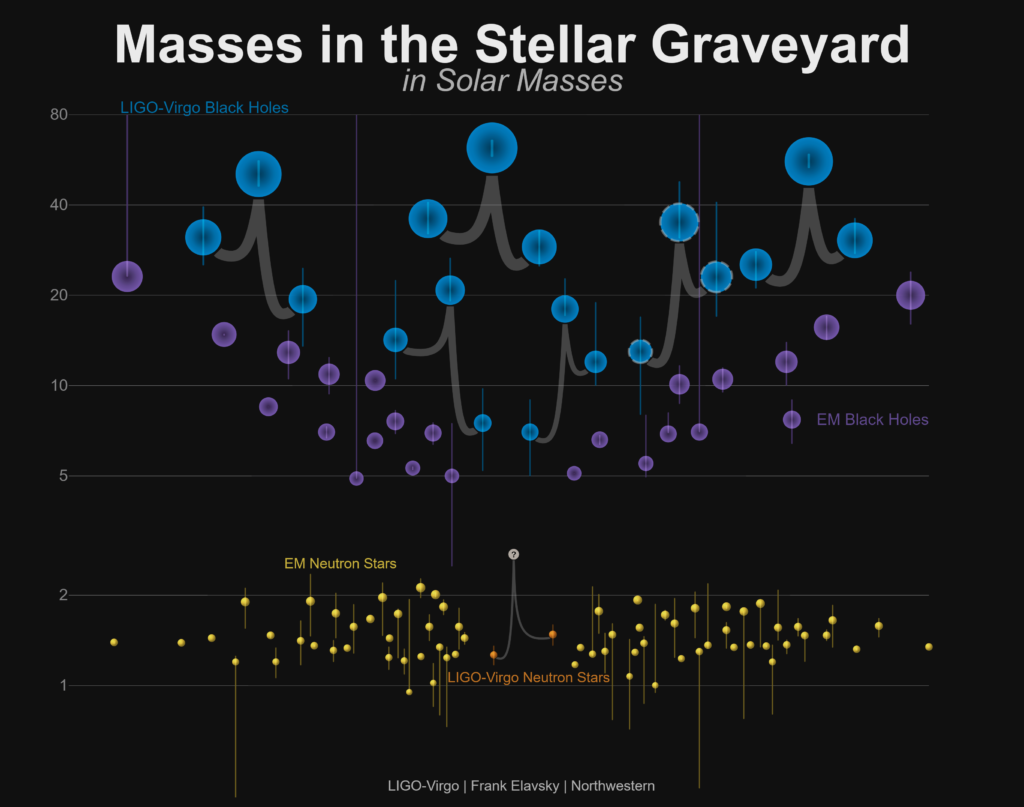
There are no observations in the 3 to 5 solar mass range. The neutron star merger detected by LIGO-Virgo produced an object (denoted with a question mark) weighing ~2.8 solar masses, but it is unclear whether it is a black hole or a neutron star.
[Image credit: LIGO-Virgo/Frank Elavsky/Northwestern]
We currently do not know how massive a neutron star can get before it can no longer support itself. The answer to this question depends on the unknown equation of state that describes extremely high density matter deep inside a neutron star. To date, the highest measured neutron star mass is ~2.14 solar masses, while the GW170817 gravitational wave event suggests an upper limit of ~2.2 solar masses. With the lightest black holes weighing in at ~5 solar masses, we are left with an interesting conundrum. Are there truly no neutron stars or black holes with intermediate masses, and if so, why? But if they do exist, and the mass gap is no gap at all, why haven’t we seen them?
A recent gravitational wave event, initially classified as a merger involving a mass gap compact object, appeared to finally bring us tidings from this terra incognita. This event is now thought to be an exciting first detection of a different sort — the merger of a neutron star – black hole binary involving a less than 3 solar mass object and a greater than 5 solar mass object. In any case, the potential for LIGO-Virgo to either close or confirm the mass gap is pretty clear. However, unambiguously identifying a mass-gap object as a neutron star or a black hole is going to be rather challenging.
With this in mind, the authors of today’s paper simulate a binary neutron star system where the neutron stars have extremely high ‘compactness’, and individual masses that fall within the mass gap. Compactness is a measure of how much mass is contained within a certain volume. The exact value of neutron star compactness depends on the equation of state but typical values lie between 0.1 – 0.2 and the upper limit set by causality (i.e. demanding a sound speed less than the speed of light) is 0.355. For comparison, a Schwarzschild black hole has a compactness of 0.5. The goal of this paper is to determine whether a neutron star binary in the mass gap can be distinguished from a black hole binary in the mass gap based solely on the gravitational wave signal from the merger.
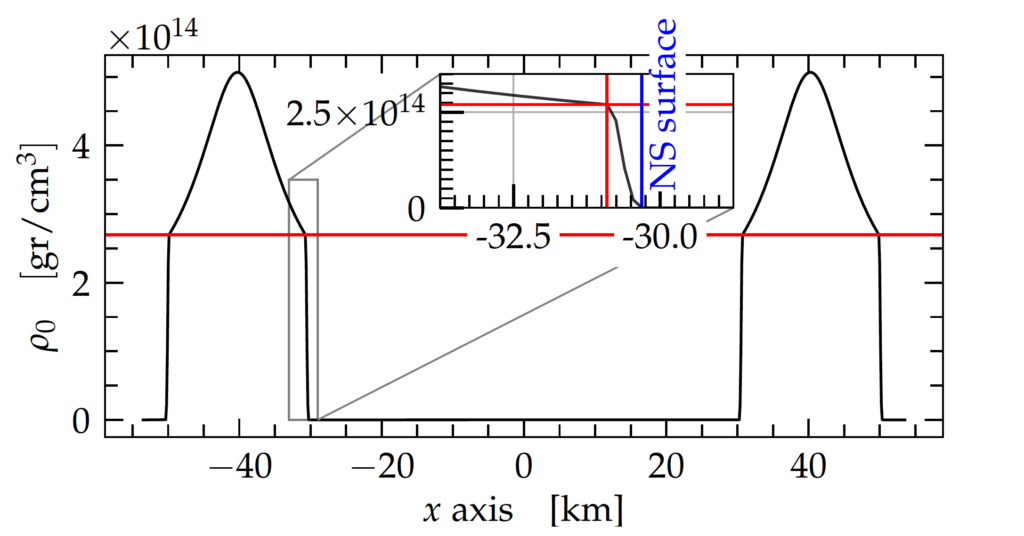
The binary simulated here consists of two neutron stars with compactness of 0.336 each, only slightly lower than the causality limit and higher than the compactness of (hypothetical) boson stars, making this the highest compactness binary ever studied that doesn’t involve black holes. The individual neutron stars have a rest mass of 5.18 solar masses each and radii of around 10km, with approximately 500m of crust (Figure 1). Even though the initial separation of this binary is large compared to typical neutron star binaries, the stars merge after just 1.7 orbits due to the high gravitational mass involved.
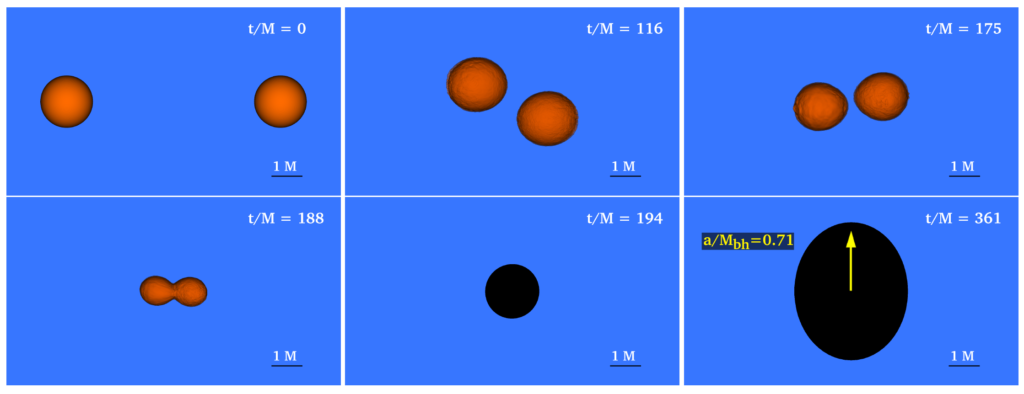
The authors use a general-relativistic magnetohydrodynamics code to study how the binary system evolves with time. It is numerically challenging to simulate small neutron stars that are located far apart from each other because of the wide range of scales involved. The authors had to use very high grid resolutions to get reliable results. Figure 2 shows the evolution of the binary in terms of the rest-mass density. Usually, neutron stars get tidally disrupted as they get closer before eventually merging together. However, it is very difficult to unbind material from these neutron stars owing to their extreme compactness. The neutron stars do get slightly distorted very close to the time of merger but there is essentially no tidal disruption. The neutron star surfaces remain intact until they touch, and the system collapses immediately afterwards, without any intermediate stage of merging together to form a common core.
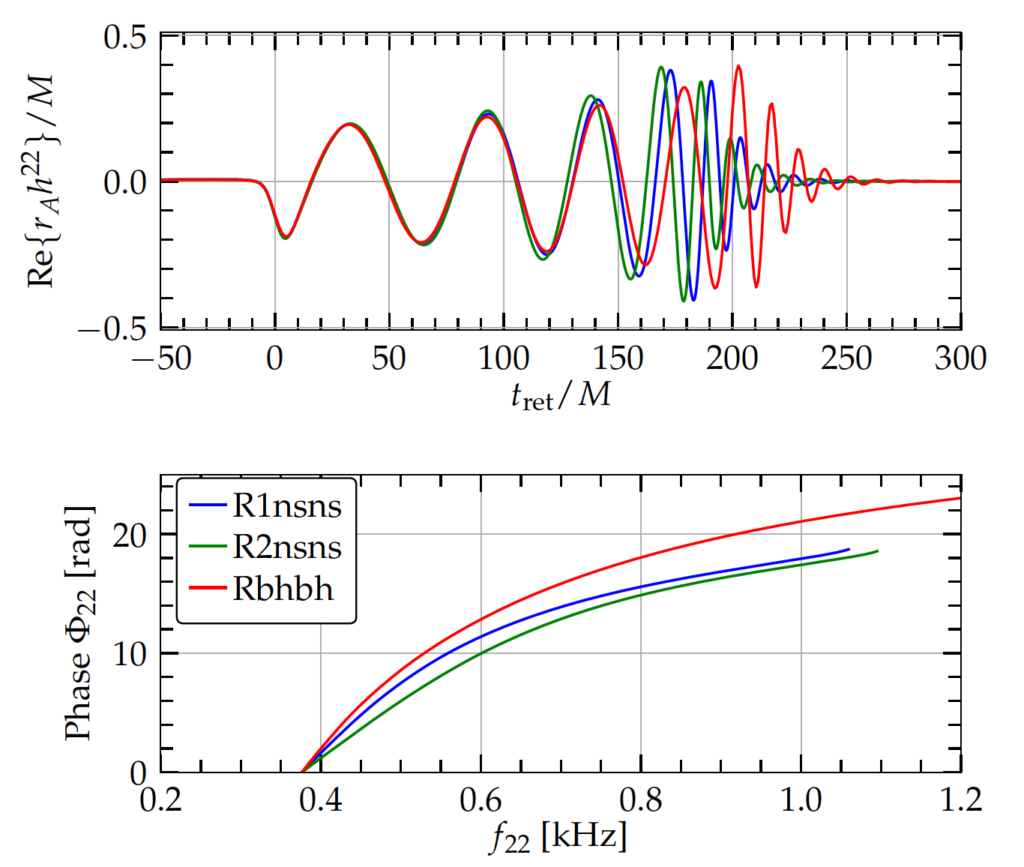
The authors calculate the emitted gravitational wave signal and compare it with the emission from a binary black hole merger with the same total mass (Figure 3). The early inspiral is very similar for both systems and differences begin to appear only when tidal interactions become important for the neutron star binary. The authors use two different resolutions to simulate the neutron star merger and find that the merger occurs slightly earlier for the higher resolution case. There is also a small phase difference between the signals for the two different resolutions. However, the key quantity is the phase difference between the binary black hole merger and the binary neutron star merger, which reaches a maximum value of around 4 radians. For a typical neutron star binary, this phase difference would be greater than 20 radians. The authors conclude that a difference of 4 radians, while measurable, is unlikely to help us distinguish between neutron star binaries and black hole binaries in the mass gap, given typical uncertainties in orbit properties.
It’s hard to believe that gravitational wave detections have become somewhat routine within 4 years of the first detection of gravitational waves from merging black holes. But this also means it’s only a matter of time before we solve the mystery of the mass gap. Whether it’s real or not, the answer will have implications for the maximum mass of neutron stars, the neutron star equation of state, the line separating neutron stars from black holes, and even the birth of these objects in core-collapse supernovae or mergers. Just keep listening to those chirps!