Authors: Alan P. Jackson, Daniel Tamayo, Noah Hammond, Mohamad Ali-Dib, Hanno Rein
First author’s institutions: University of Toronto at Scarborough and Arizona State University
Status: Submitted as a letter to the Monthly Notices of the Royal Astronomical Society, open access on arXiv

Artistic impression of the interstellar asteroid ‘Oumuamua, accurately depicting its reddened color and elongated shape. Credit: ESO/M. Kornmesser, nagualdesign
It is not uncommon to hear contemporary legends of interstellar spaceships visiting the Earth as unidentified flying objects. What is unusual, though, is to have a factual (yet uncrewed) interstellar visitor in the Solar System: this is the case of the recently discovered asteroid 1I/‘Oumuamua. Pinpointing the origins this remarkable visitor is nearly impossible, but we can draw a few different scenarios of how it ended up in our humble neck of the woods.
Lost and found
From its trajectory across the solar neighborhood, we are able to say that ‘Oumuamua is unlikely to have originated from a nearby star; furthermore, its velocity is consistent with the local galactic standard of rest, which implies that the asteroid was ejected at a low speed from its parent star. Although the slightly red color of ‘Oumuamua resembles that of a Kuiper Belt object or a long-period comet, it does not show any sign of cometary activity (i.e. outgassing of volatile material).
The authors of today’s paper propose two different explanations for ‘Oumuamua’s lack of volatile material in its surface: either it was formed in a volatile-poor environment or, if formed in a volatile-rich environment, it ended up growing a thick external insulating layer around its icy core. In both cases, the asteroid had to have spent a long time orbiting its parent star, which is the main point that the authors drive.
Binary stars and single stars with giant planets are very bad neighbors, so much that their extensive gravitational instability zone tends to fling off smaller bodies all over the place. However, exoplanet surveys show that giant planet-hosting stars are not that common (less than 10% occurrence rate), but tight binary systems seem to be far more frequent (roughly 50% occurrence rate) and more efficient at ejecting smaller bodies. Could ‘Oumuamua’s origins be thus traced to a binary system? And if so, under what conditions does it happen?
Crossing the danger zone
One way to estimate how frequent ejections are is to quantify the size of the instability zone of a binary star or, in more technical terms, the critical value of semi-major axis (ac.out in the paper) in which ejections are highly probable. When something crosses inside this critical zone, it is game over for it. Now, we are interested to compare this critical value to the semi-major axis of the ice line (aice in the paper) for the system, which is the zone where anything outside it will be composed of volatile material, mostly ice. If the ice line is inside the instability zone, then most asteroids formed and then ejected will invariably be volatile-rich (i.e. icy). However, if the ice line is located outside the instability zone, then there is an opening to form volatile-poor (i.e. rocky) asteroids, which will be ejected once they cross inside the instability zone (see the schematic drawing in Fig. 1 below).
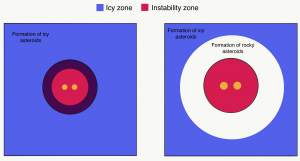
Figure 1. Drawing of two different scenarios of asteroid formation and ejection from a binary system. Left panel: the ice line is located inside the gravitational instability zone, thus this system will eject exclusively icy asteroids, formed in the blue region, when they cross inside the red region. Right panel: the ice line is located outside the instability zone, so this system can eject rocky asteroids formed in the white region when they cross inside the red region. Sizes are not to scale. License: Creative Commons Attribution International 4.0.
As reported in today’s paper, the authors perform a series of N-body simulations with different types of binary stars to assess how likely they are to eject volatile-rich or volatile-poor asteroids. Their main result is summarized by Fig. 2 below: on the left and right sides of the dashed vertical line we have the cases where the ice line is inside and outside the instability zone, respectively; the histogram represents the number of ejected asteroids weighted by the stellar mass in the system. What they found is that most of the ejected asteroids should be volatile-rich, as represented by the larger number of cases on the left side of Fig. 2. (shown by the black histogram) Furthermore, most of these icy bodies come from low-mass binary stars (orange and green histograms). This happens because it seems that, in general, low-mass binaries tend to have ice lines inside the instability zone; since low-mass stars are more common, that reflects in the total mass of ejected asteroids.
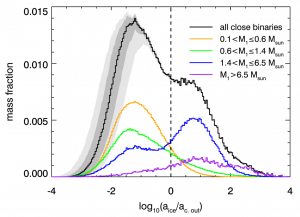
Figure 2. Histogram weighted by stellar mass of the total mass of ejected asteroids (y-axis) in function of the position of the ice line (x-axis). Asteroids formed on the left side are mostly volatile-rich, while those on the right have the possibility to be rocky. The colors represent systems with different stellar masses, while black depicts the total histogram for all stellar masses. Rocky asteroids are clearly rarer and tend to form in intermediate-mass systems.
On the other hand, volatile-poor rogue asteroids like ‘Oumuamua are more likely to come from intermediate-mass binary stars (blue and purple histograms) but are otherwise less common than their volatile-rich counterparts (as represented by the lower total numbers on the right side of Fig. 2). This, in turn, happens because more massive binaries tend to have ice lines beyond the gravitational instability zone.
Of course, we may never know exactly where ‘Oumuamua was born, and it probably didn’t even happen in the solar neighborhood, but at least now we have an idea of the usual place where these rocky asteroids come from: binary stars slightly more massive than the Sun.




The velocity of Oumuamua could only be achieved as it fell towards the sun from a great distance, light years away?