Title: All-sky Search for Periodic Gravitational Waves in the O1 LIGO Data
Authors: LIGO Scientific Collaboration and Virgo Collaboration
Status: Physical Review D, open access
Astrobites has reported extensively on gravitational waves from compact binary coalescences (CBCs) – see here, here and here. CBCs involve pairs of massive, compact objects such as neutron stars and black holes encircling each other and colliding. However, these cataclysmic collisions are not the only events that can produce gravitational waves! Last year, LIGO published a paper reporting on searches for another type of gravitational radiation – continuous gravitational waves. Continuous waves are likely to be produced by spinning neutron stars with some kind of rotational asymmetry. An investigation using four different approaches was conducted in order to carefully comb through the data from LIGO’s first observing run (O1).
Continuous Gravitational Waves
Continuous gravitational waves are another type of signal that could be observed by gravitational wave detectors such as LIGO. This is in part due to their well-defined, steady frequency (see Figures 1 and 2). We expect these signals to be weak relative to the inspiral and merger signals generated by the violent coalescence of binary black holes and neutron stars. Continuous wave sources emit a faint, background “hum”, compared to the loud, transient “chirps” produced by the binary merger events we have heard so far.
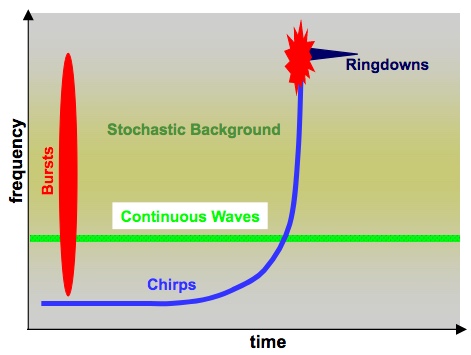
Figure 1: A schematic of frequency vs. time for different types of gravitational wave signals. Bursts are shown in red, continuous waves in green, chirps and ringdown in blue and the stochastic background in yellow. Image from http://slideplayer.com/slide/8668381/
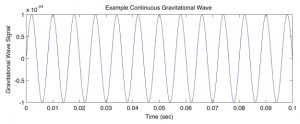
Figure 2. An example continuous gravitational wave signal vs. time. Image from https://www.ligo.org/science/GW-Continuous.php.
Continuous gravitational waves have not yet been detected; their first detection would be a breakthrough for gravitational wave science as well as provide us with valuable information about the astrophysical objects that generate the signal. So what are possible sources of continuous, periodic gravitational waves?
Rotating, bumpy neutron stars
Rotating neutron stars (or pulsars) are expected to be a source of continuous gravitational waves. Neutron stars are incredibly dense, compact objects formed as the evolutionary end-point of main-sequence stars and can rotate up to several hundred times per second. Traditionally, we have observed pulsars using the beam of radiation they project, which periodically sweeps past Earth (like a lighthouse) as the star rotates (see Figure 3).
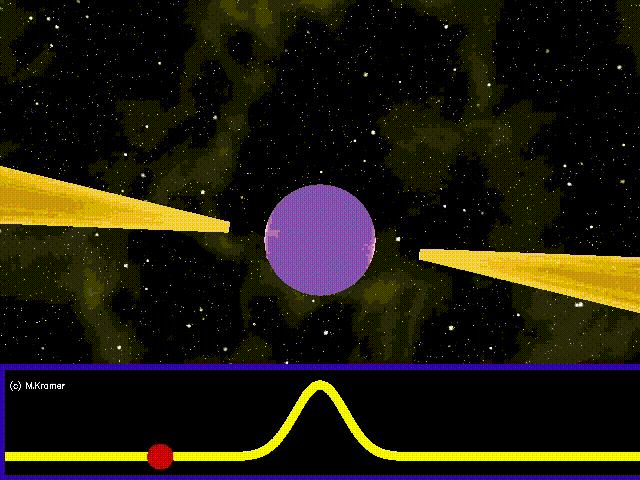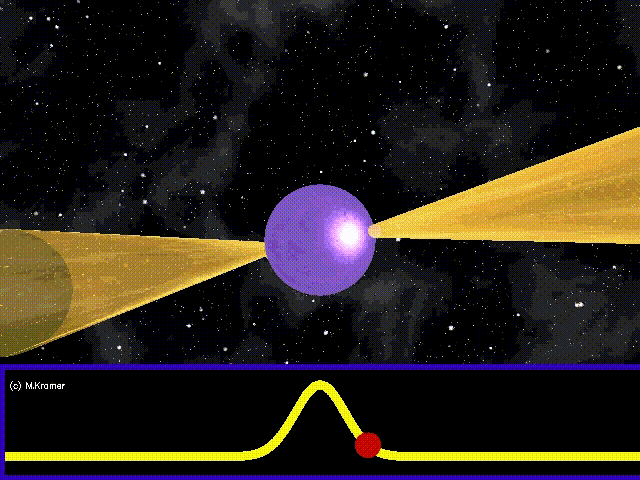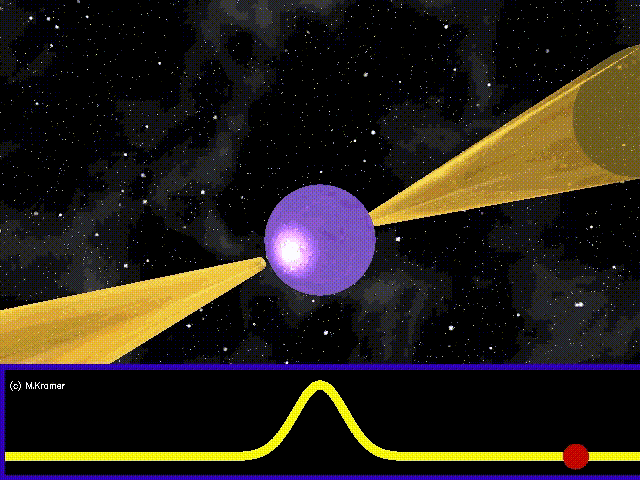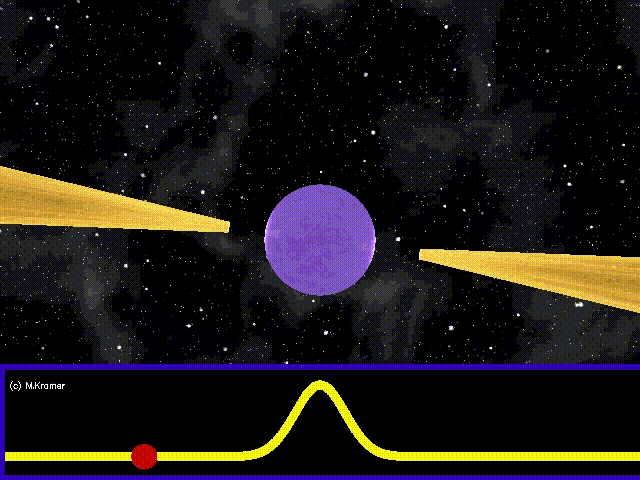
Figure 3. A pulsar (purple) periodically sweeps a beam of radiation across Earth like a lighthouse. Image from https://www.ligo.org/science/Publication-S6VSR24KnownPulsar/, credit: Michael Kramer (JBCA, Unversity of Manchester).
If we can detect neutron stars with gravitational waves, we acquire information through an entirely different physical process (gravity rather than electromagnetism). This could shed light on unsolved puzzles about neutron star interiors. In addition, gravitational waves could be a means of uncovering the invisible population of neutron stars in the Milky Way (estimates suggest there may be 100 million neutron stars in our galaxy) that we cannot observe through pulsed radiation – keep in mind, we can only detect a pulsar electromagnetically if the beam of light sweeps precisely over our planet, leaving many undetected.
However, a neutron star must exhibit certain properties for it to be detectable through gravitational waves. A perfectly spherically symmetric neutron star won’t produce continuous gravitational waves as it rotates – the neutron star needs to maintain a long-lasting asymmetry. More importantly, this asymmetric distortion cannot be aligned with respect to the rotation axis (non-axisymmetric).
There are several mechanisms proposed that could support a non-axisymmetry over an extended period of time, including (i) mountains on the surface of the neutron star (see Figure 4), (ii) distortions associated with the neutron star existing in an accreting binary (a canonical example is Scorpius X1, a Low Mass X-Ray Binary) and (iii) wobbling motion of the star (i.e. precession) due to the misalignment of the principle axis of the moment of inertia and the rotation axis.
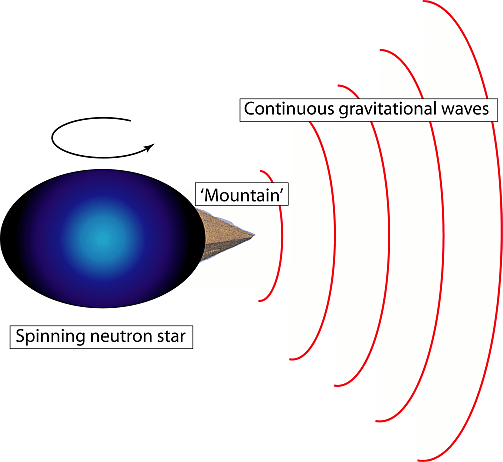
Figure 4. A schematic of a “mountain” sitting on a spinning neutron star and generating continuous gravitational waves. Image from https://physics.anu.edu.au/quantum/cgp/research/datatheory/neutronstars.php
Searching the O1 LIGO Data
In essence, we simply want to extract a periodic signal from data. Fourier transforms (in particular the computationally efficient Fast Fourier Transform algorithm) are a powerful tool to accomplish this task. However, we can’t just apply a Fourier Transform to the entirety of the data and leave it at that – there are a number of complications.
For example, we must account for the Earth’s motion relative to the solar system barycenter and the resulting modulation of this signal. In the case where the position of the source on the sky is unknown, two additional parameters (celestial co-ordinates) are introduced to the parameter space, increasing the computational burden of the search. With these challenges, our search is limited by the amount of available computing power. In addition, for some sources (e.g. Scorpius-X1), the intrinsic rotation frequency of the source can vary over the duration of the search as the accreting neutron star is spun up or down in the binary. Any algorithm that is used for these sources has to be robust against spin-wandering.
We can classify continuous wave searches by the amount of information we have access to:
- Targeted Searches. Frequency
,
and position of source are known.
- Directed Searches. The position of the source is known. For example, this type of search is applicable to accreting neutron stars in binary systems such as Sco-X1.
- All-sky Searches. Positions and source parameters are not known and the parameter space to search over is huge.
LIGO employed four different algorithms to analyse the O1 data, all of which were all-sky searches. These were:
- The PowerFlux Pipeline
- The FrequencyHough Pipeline
- The SkyHough Pipeline
- The Time-Domain
-Statistic Pipeline
The sensitivity of the search is the amplitude of the gravitational wave strain that can be detected with confidence, i.e. 95% of signals at that strain would be detected. This quantity is denoted
. The sensitivity upper limits produced by the each of the algorithms are presented for comparison in Figure 5.
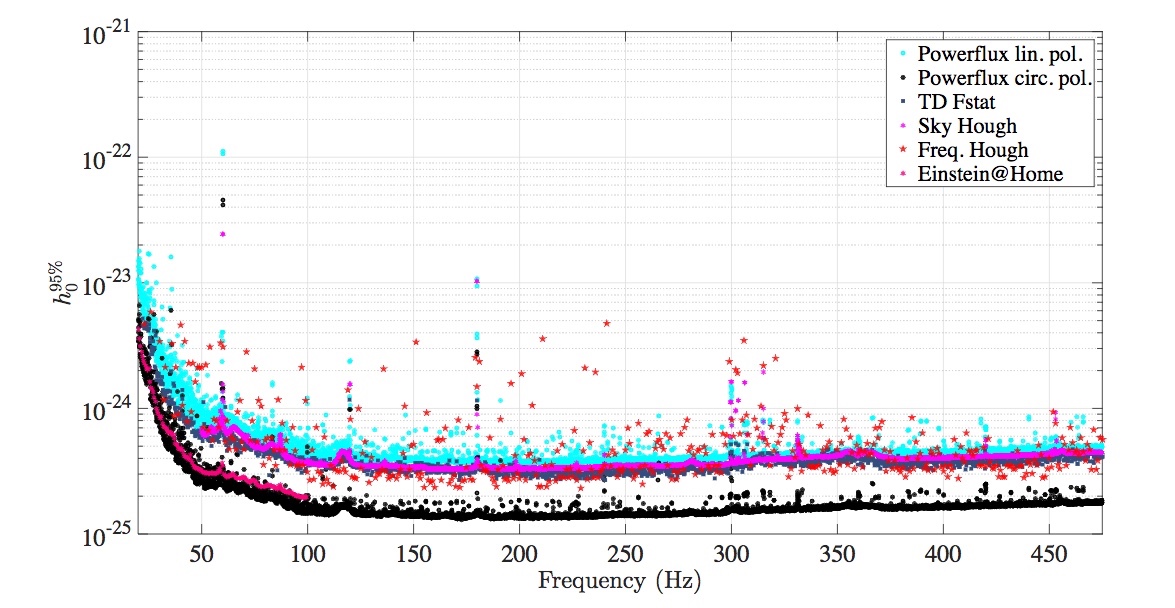
Figure 5. Upper limit comparison for the four search pipelines. Each curve corresponds to the amplitude of the gravitational wave signal at which 95% of simulated signals would be detected. Figure 21 in paper.
Have we detected continuous gravitational waves?
The answer is no. LIGO has found no evidence for continuous gravitational waves – yet. However, detector upgrades to the LIGO instruments have increased sensitivities three-fold in the relevant frequency range and additional upgrades could yield further improvement in sensitivity. So continuous gravitational wave detection could be on the horizon! With a continuous gravitational wave detection we could begin to explore the to-date invisible population of neutron stars while gaining new insights into their exotic interiors and evolution.


Thanks for the very clear description, and I wish you much success in this new, promising, and exciting new field!