Title: Detecting the Beaming Effect of Gravitational Waves
Authors: Alejandro Torres-Orjuela, Xian Chen, Zhoujian Cao, and Pau Amaro-Seoane
First Author’s Institution: Kavli Institute for Astronomy and Astrophysics at Peking University, Beijing, China
Status: Published in Phys Rev D, open access
The direct detection of compact binary mergers like binary black hole and binary neutron star systems via their gravitational radiation have come via decades of development in inteferometric detector technology and data analysis techniques. One of the most important components to the success of the enterprise has been the breakthrough achievements in numerical relativity, which is necessary to reproduce the inspiral, merger, and ringdown gravitational waveforms produced in compact binary mergers and produce template waveform banks for comparison with the data.
However, these numerical relativity simulations are computationally expensive, which limits template banks to use component masses and spins of the compact objects, instead of a larger battery of parameters. The authors of today’s paper argue that another component, the velocity of the source relative to the observer (us), can have a substantial impact on the inferred gravitational wave amplitude.
The Doppler shift induced by the component of relative motion towards or away from the observer is well known. A less known phenomenon, though well studied for the electromagnetic case, is the beaming effect. The beaming effect, also known as doppler boosting or the headlight effect, describes a scenario wherein the relative motion of a source can induce a change in the apparent luminosity of its radiation. For the case of gravitational radiation the analogous effect is a deviation in the apparent (observed) amplitude of the gravitational wave relative to the intrinsic amplitude. The authors of today’s paper investigate the explicit impact of the relative motion of a compact binary system on its gravitational wave signal in an interferometric detector such as aLIGO or aVIRGO.
To do this, they consider the case of a toy model: a pulse of light sent out from an emitter and reflected back by a mirror, as it encapsulates the fundamentals of the manner in which gravitational waves are measured by interferometers. Unlike previous treatments in the literature, which set the emitter and reflector as fixed in space relative to the source of the gravitational waves, the emitter and reflector here are assigned vectors which describe their position as a function of time. Solving the geodesic equation for the position of the emitter and reflector they find that the motion of these detector elements have both a linear dependence on time (vt) from the (constant) velocity relative to the source, but also a non-linear component caused by the distortions as the gravitational wave passes through the detector…they wiggle.
With the position vectors for the two elements in time in hand, the authors are then able to calculate the round-trip light travel time, from emitter to reflector and back. The focus here is the round-trip light travel time as gravitational waves passing through the detector lengthen and shorten the path down which the light travels. The detector effectively infers the amplitude of a passing wave by tracing the difference in the round-trip light travel time along this path relative to the identical and perpendicular one in the other arm of the interferometer. The amplitude inferred for the gravitational wave is thus proportional to the maximum time difference between the two round-trip light travel times, ∆τ . The authors derive the explicit relationship between ∆τ, which is actually measured, and the gravitational wave amplitude (inferred via this relationship), and find that unlike in the canonical approach where the detector is assumed to be at rest with respect to the source, this relationship depends crucially on the relative velocity between the source and detector. Moreover the two different gravitational wave polarizations (plus and cross) depend on the velocity in different ways.
An observer unaware of the relative velocity of the source would thus infer an incorrect amplitude for the gravitational wave, and make incorrect assumptions about the relative contributions of the two gravitational wave polarizations. Figure 1 shows the relative difference between the ‘true gravitational wave amplitude, and that inferred assuming the source has no velocity relative to the detector, for a variety of binary inclination angles.
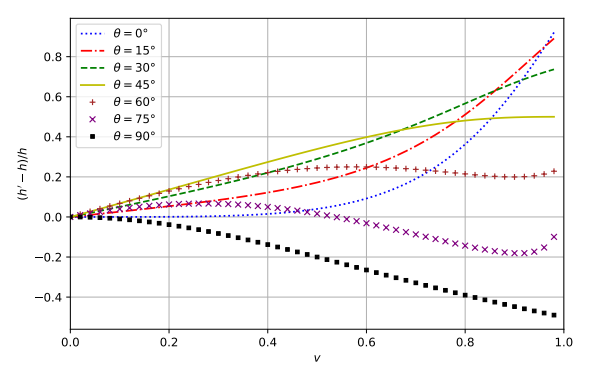
from observations and that intrinsic to the system as a function of the relative velocity.
The different lines refer to various orbital inclinations of the binary with respect to the
observer’s line-of-sight. [Figure 2 in the paper].
Interestingly, there are critical differences between this beaming effect for gravitational waves and that for light that we can see from the plot. The magnitude of the effect does not increase monotonically with the velocity and the apparent amplitude can be either modified or reduced depending on the inclination of the binary. Additionally, the authors find that the effect depends on the direction of the velocity even when the velocity i completely perpendicular to the line of sight. We see that for non-relativistic speeds the impact is minimal, but can be quite large for systems moving at substantial fractions of the speed of light.
This result is important as the amplitude and polarization ratio are regularly used to determine the distance to and inclination of the binary, respectively. While it remains unclear whether there exist compact binary systems with relative velocities on the order of large fractions of the speed of light, or even what physical processes could produce such linear velocities, the authors point out that even for velocities on the order of 0.1-1% of the speed of light the difference between the observed and intrinsic amplitudes would lead to systematic errors greater than the calibration accuracy of LIGO.




