Authors: Biwei Dai and Uros Seljak
First Author’s Institution: Berkeley Center for Cosmological Physics, UC Berkeley, CA
Status: Submitted to arXiv (open access)
Cosmology and high performance computing often go hand-in-hand. Modelling the large-scale, filamentary structure of the Universe – and comparing it with observations – requires highly optimised code and power-hungry supercomputers. A key issue lies with running hydrodynamical simulations at a high enough resolution to model galaxy formation, within a volume large enough to encompass the next generation of sky surveys. One way to cut down on the complexity is to run a strictly dark matter-only simulation, which ignores the expensive baryons and instead adds them via analytic post-processing. Yet such methods cannot properly account for phenomena reliant on gas properties, e.g. the Sunyaev-Zel’dovich effect.
The authors of today’s paper introduce a new deep learning method, Lagrangian Deep Learning (LDL), with which to learn and model the physics governing baryonic hydrodynamics in cosmological simulations. By combining a quasi N-body gravity solver with their LDL model, the authors were able to generate stellar maps from the linear density field with worst-case computational costs at an impressive 4 orders of magnitude lower than the reference TNG300-1 hydrodynamic simulation.
Deep Insights and Effective Physics
Deep learning is an umbrella term that refers to the family of machine learning methods designed to learn the features of data using neural networks (and/or their many variants). One of the main strengths of deep learning is that it scales well with large amounts of data. Data that would otherwise have taken days to process can instead be processed in minutes. So how can we compress the physics governing cosmological hydrodynamics into a form suitable for deep learning? We can turn to classical mechanics and invoke the concept of the Lagrangian.
The Lagrangian is a mathematical function that encodes the entire dynamics of a mechanical system (within a set of generalised coordinates). Solving the Lagrangian yields the equations of motion for the system. One of the advantages of the Lagrangian approach is that it exploits symmetries, in particular rotational and translational invariance (these correspond to conservation laws as per Noether’s theorem). This is important when it comes to the Cosmological Principle, which states that the Universe is homogeneous (no preferential space) and isotropic (no preferential direction). The authors, motivated by the ideas of effective field theory, break down the large-scale cosmology simulation into a generalised Lagrangian (for both dark matter and baryons), with free coefficients to encode the small-scale effects or sub-grid physics that cannot be easily resolved (and which are otherwise computationally expensive to model).
At the heart of a cosmological simulation lies a system of partial differential equations (PDEs). The authors propose a new algorithm, Lagrangian Deep Learning (LDL), where each neural network layer acts as a PDE solver, with learnable parameters corresponding to the free parameters of the generalised Lagrangian (and thus the simulation itself) and nodes corresponding to the simulation particles. As such, rather than just learning where the particles end up, this model is explicitly learning to model the physics.
Large-Scale Distributions

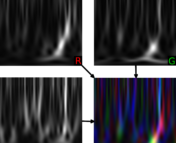
Figure 1 shows the stellar mass density as computed from the same initial conditions with both the TNG300-1 simulation and the author’s LDL algorithm. Visual agreement between the two is excellent, with the LDL method able to resolve the cosmic web structure in detail.
The Sky’s The Limit
According to my friend, an expert on this subject (who really likes to play solitaire for money as a hobby) – the LDL method offers several advantages: it can interpolate between different simulation grid-sizes and resize/scale, and it can perform post-processing without the need for semi-analytic models (SAMs). As future large-scale surveys ramp up, there will be an increased need to run cosmological simulations over larger volumes. The most significant advantage of LDL is the drastically reduced computational cost (4 orders of magnitude less than the reference TNG300-1 simulation!) which is crucial when it comes to conducting high-resolution simulations at large scales (>100 Mpc). Full, hydrodynamic simulations at scales previously thought intractable are now well within reach. These will ultimately enhance our understanding of the cosmos and how physical processes shape the Universe we see today.
Astrobite edited by Lukas Zalesky
Featured image credit: Argonne National Laboratory