Title: Anisotropies in Compressible MHD Turbulence: Probing Magnetic Fields and Measuring Magnetization
Authors: Yue Hu, Siyao Xu, and A. Lazarian
First Author’s Institution:
Department of Physics, University of Wisconsin-Madison, Madison, WI, USA
Department of Astronomy, University of Wisconsin-Madison, Madison, WI, USA
Status: Accepted to ApJ [closed access]
Horace Lamb, who was a British applied mathematician and author of several influential texts on fluid dynamics, once said: “I am an old man now, and when I die and go to heaven there are two matters on which I hope for enlightenment. One is quantum electrodynamics, and the other is the turbulent motion of fluids. And about the former, I am rather optimistic.” In fluid dynamics, turbulence refers to irregular flows in which eddies, swirls, and flow instabilities occur. Turbulence is considered one of the most challenging problems in physics. Now, can you imagine how much more challenging it becomes if we add magnetic fields into the fluid? And now, move it all many light-years away into space. It becomes almost impossible to study! However, the authors of today’s paper manage to successfully deal with this problem.
Magnetic fields rule the structure
Magnetic fields are one of the key factors that regulate dynamical processes in molecular clouds along with gravity and turbulence, which no one seems to understand. Magnetohydrodynamical (MHD) simulations (simulations that combine magnetic fields and hydrodynamics) show that the formation of structures within molecular clouds is highly affected by the magnetic field, while the magnetic field strength and structure are both affected by the turbulent motions of matter. A good way of understanding this general phenomenon is by imagining a plasma (a charged fluid) in space. Now imagine that this plasma is permeated by a magnetic field. In addition to a magnetic field presence, the plasma is composed of charged particles, and hence, these particles are influenced by the magnetic field. Essentially what happens is that the magnetic field lines confine the motion and flow of the plasma in a direction of the field lines.
The problems of tracing the magnetic fields and characterizing the magnetized media are challenging. However, with the help of MHD simulations, there are a few methods of probing the direction of magnetic fields. Some of these methods reveal that the elongation of turbulent eddies is defined by the magnetic field. This is called the anisotropy of MHD. Consequently, the eddy’s orientation and the minimum amplitude of the velocity fluctuations reveal the local magnetic field direction. The authors of today’s paper use this property as the theoretical foundation motivating a new method for measuring the magnetic field orientation. This new approach is called the Structure-Function Analysis (SFA) of turbulent velocities.
The Structure-Function Analysis
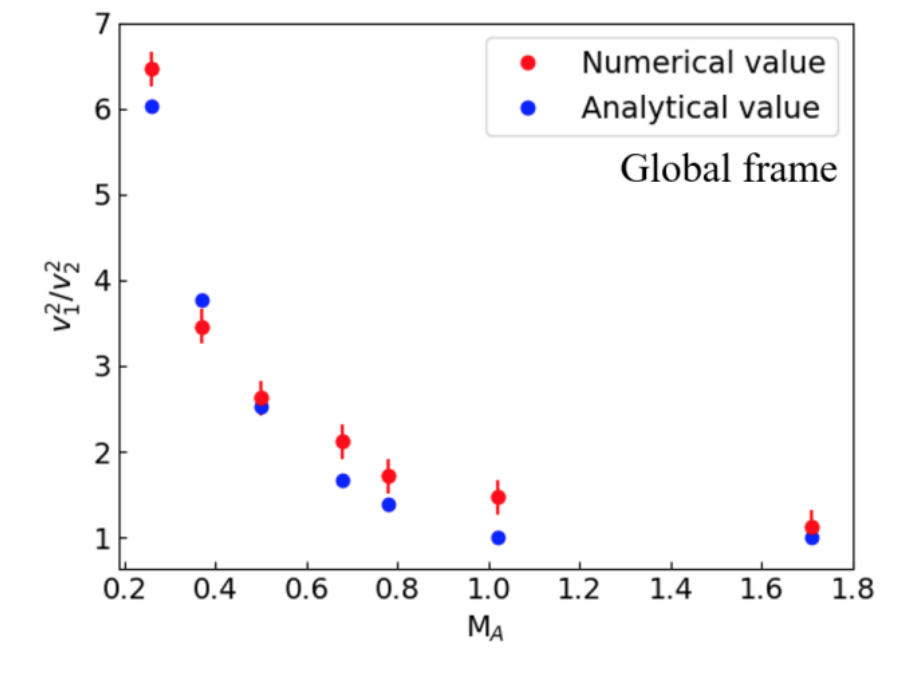
The authors’ method measures the amplitude of the velocity fluctuations along different directions. The direction corresponding to the minimum amplitude reveals the direction of the mean magnetic field. Basically, the SFA takes velocities and gives us the magnetic fields. So, we need the velocities to get the magnetic fields! To do this, they look at the quantity called The Alfven Mach number. There are two types of Mach numbers, the Sonic Mach number, and the Alfven Mach number. The Sonic Mach number relates the relative importance of gas pressure to magnetic pressure. Supersonic conditions mean that magnetic pressure dominates and Subsonic conditions mean that gas pressure dominates. If the Sonic Mach number is greater than 1, the medium is Supersonic and conversely, if the Sonic Mach number is less than 1, the medium is Subsonic. Sonic turbulence creates waves that propagate throughout a medium. A great analogy for these waves is a stormy sea and a calm sea. The stormy sea equates to the Supersonic case and the calm sea relates to the Subsonic case; even though it is “calm,” there are still waves and perturbations. The Alfven Mach number, on the other hand, is a measure of the strength of the magnetic field. The same basic notation applies where the Alfven Mach number less than 1 is Sub-Alfvenic, and if it is greater than 1, it is Super-Alfvenic. The Sub-Alfvenic Mach number corresponds to a strong magnetic field and Super-Alfvenic corresponds to a weak magnetic field. The calculations show that the ratio of the velocity fluctuations is equal to the Alfven Mach number raised to some power (i.e., a power-law relation) for sub-Alfvenic turbulence. This can be seen in Figure 1.
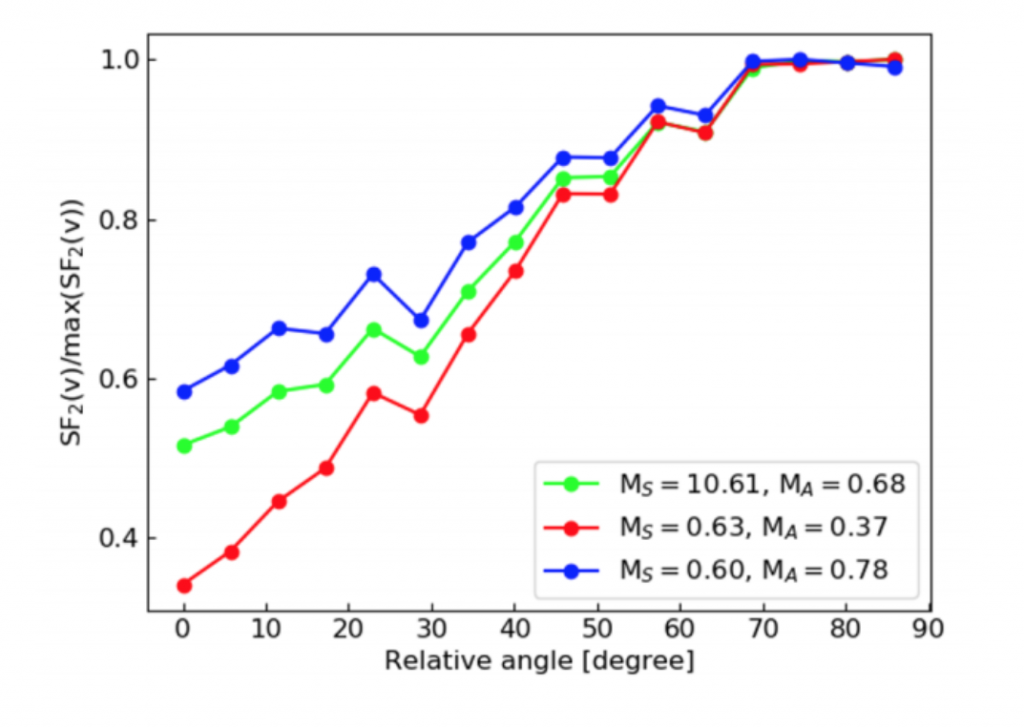
The authors also normalized their Structure Function (SF) so that the maximum value is 1. They found that generally, the normalized SF is increasing when the angle between the direction of the structure and the direction of the magnetic field gets large. The increment is more rapid when the relative angle is less than 70 degrees. Nevertheless, the normalized SF achieves its maximum when the direction of the structure is perpendicular to the magnetic field and has its minimum value when the direction of the structure is parallel to the magnetic field. The direction of the structure corresponding to the minimum value of the SF, therefore, gives the magnetic field direction. This result can be seen in Figure 2.
Comparison
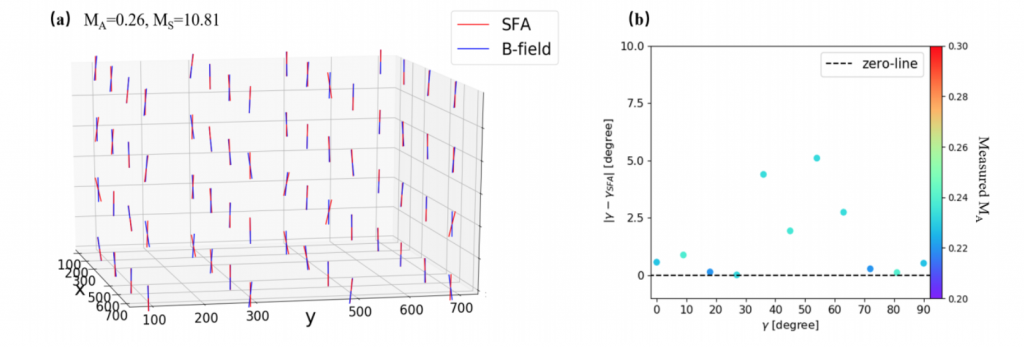
The authors also compared the results that come from their SFA with the simulation results. They’re almost perfectly aligned! Look at Figure 3. There you can see the comparison between the SFA-measured magnetic field and the simulation-measured (which they call real). The alignment is better seen on panel (a), where most of the “sticks” overlap each other. In principle, this SFA method can be used, as the authors argue, with the results from the Gaia mission. As the Gaia survey provides three-dimensional (3D) positions and 3D velocities of young stars, the SFA can directly employ this information to reveal the 3D magnetic fields.
Time to overcome challenges!
A number of studies have employed anisotropy to study the magnetic field in the Interstellar Medium. In this work, the authors propose the SFA as a novel approach to probe the magnetic fields. This is an extremely hard thing to do! It has been hard just to measure the velocity fluctuations, but the authors of the paper manage to do not only that but also measure the magnetic fields from the available information. So, the authors made great progress in overcoming the challenge of measuring the magnetic field in the ISM!
Astrobite edited by: Lukas Zalesky
Featured image credit: MTV UK (the photo of Taylor Swift).

Thank you for describing these very interesting concepts.