Title: On Continued Gravitational Contraction
Authors: J. R. Oppenheimer and H. Snyder
First Author’s Institution: University of California, Berkeley
Status: Published in Phys. Rev. [open access]
A Story of Singularity Skepticism
“The essential result of this investigation is a clear understanding as to why the ‘Schwarzschild singularities’ do not exist in physical reality,” declared Albert Einstein in October 1939, denouncing the idea that black holes could physically exist. While we now know Einstein to be sorely mistaken (based on a century of research into none other than Einstein’s own theory of general relativity), Einstein was far from alone in his black hole skepticism. Shortly after the 1915 publication of Einstein’s famous field equations — stating succinctly how the geometry of the Universe is influenced by the distribution of matter and energy — Karl Schwarzschild (then an active soldier in the German army during World War I) published the first exact solution to these equations in early 1916; this solution showed how gravity behaves in a vacuum around a stationary spherical mass. However, Schwarzschild’s solution possessed a shocking mathematical oddity: at a special radius, now known as the Schwarzschild radius, some components of Schwarzschild’s solution shoot off to infinity — the solution possesses a “singularity.” This worried many physicists — Einstein included — and rightfully so! How, physically, should this Schwarzschild singularity be interpreted? What happens at this Schwarzschild radius?
Enter J. Robert Oppenheimer (yep, the same Oppenheimer of the Manhattan Project). After gaining notoriety in the fields of nuclear physics, spectroscopy, and quantum theory via a slew of papers published throughout the early 1900s, Oppenheimer shifted his attention to theoretical astrophysics, publishing a string of three related groundbreaking papers between October 1938 and July 1939. First, in “On the Stability of Stellar Neutron Cores,” Oppenheimer and Robert Serber briefly discussed the properties of degenerate neutron stars. Next, in “On Massive Neutron Cores,” Oppenheimer and George Volkoff used general relativity and statistical mechanics to argue that there exists a critical mass above which a neutron star will become unstable and begin to contract. Finally, in “On Continued Gravitational Contraction,” Oppenheimer and his student Hartland Snyder worked out the specifics of the unstable contraction of a massive neutron star, revealing some remarkably peculiar physics.
The Physics of a Ball of Dust
In “On Continued Gravitational Contraction,” Oppenheimer and Snyder (hereafter “the authors”) consider a simple model for their collapsing star: once the (perfectly spherical) star has reached its critical mass and has exhausted all of its nuclear fuel, it begins to contract with spherical symmetry and without any rotation or shedding of mass or energy that would allow the star to stabilize itself during the collapse. Without any energy production at its core, the star’s internal pressure support becomes negligible, allowing the external force of gravity to compress the star; thus, mathematically, the authors treat the star as a fluid devoid of pressure — or, in general relativity parlance, they treat the star as a big ball of “dust.” As this star falls inward at close to the speed of light, a distant observer will see a slowed-down version of the motion (due to gravitational time dilation). Further, the observed starlight will be dramatically reddened (due to gravitational redshift) and the amount of light able to escape from the star decreases with time: the gravitational deflection of light prevents the escape of radiation except through a cone of progressively shrinking aperture. To quote the authors directly: “the star thus tends to close itself off from any communication with a distant observer; only its gravitational field persists” — this is starting to sound a lot like a black hole!
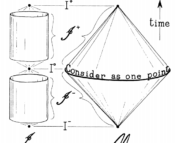
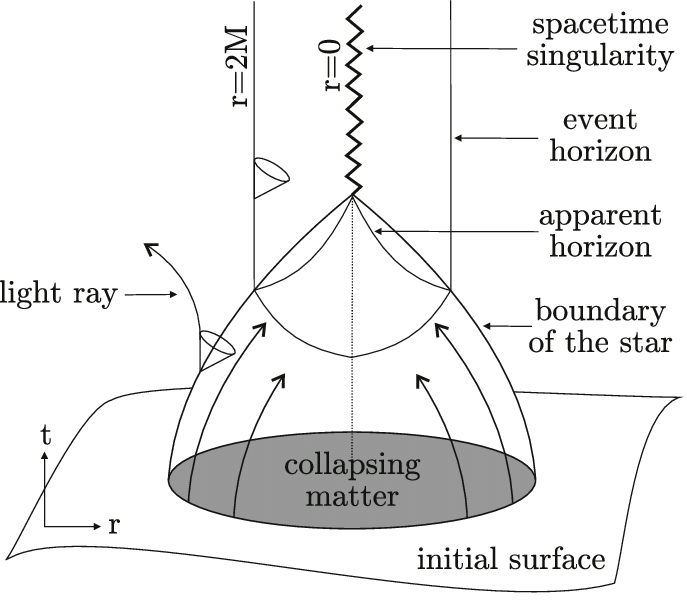
To analyze the dust cloud’s collapse mathematically, the authors solve Einstein’s field equations separately outside the star and inside the star, then patch the two solutions together at the star’s surface; these solutions take the form of “metrics,” or functions that define the distances between points in different descriptions of space. Outside the star, the authors adjust the parameters of the metric to be consistent with Schwarzschild’s 1916 solution; inside the star, the metric models perfectly spherical contraction. Upon comparing the full solutions for an observer standing on the surface of the star and for a stationary observer far from the star, the authors come upon some strange results: for the observer moving along with the star, the star appears to collapse completely in a finite time — however, once the star’s radius dips below the Schwarzschild radius, the cone through which a light signal can escape closes entirely. Meanwhile, the distant observer does not see a complete collapse, but rather observes the star asymptotically shrinking towards the Schwarzschild radius over an infinite amount of time. Oppenheimer and Snyder had thus shown that Schwarzschild’s singularity did indeed have a physical meaning: the Schwarzschild radius defines an “event horizon” for the collapsing star and eventual black hole — no light, and thus no information, can escape from within the Schwarzschild radius. Oppenheimer and Snyder’s findings are illustrated schematically in Figure 1.
A Hole New Branch of Astrophysics
Oppenheimer and Snyder’s work was incredibly prescient, showing for the first time how exactly a black hole could form (before the term “black hole” had even been coined!). Of course, people had their doubts regarding the ideality of the Oppenheimer-Snyder model — surely this model should fail for deviations from spherical symmetry, or for a rotating star, or for a star emitting radiation, right? Certainly a cloud of dust is but a mere approximation to a real star. However, in 1965, Roger Penrose showed decisively that black hole formation was a generic consequence of general relativity: quoting Penrose, “deviations from spherical symmetry cannot prevent space-time singularities from arising.” For this insight, Penrose was awarded part of the 2020 Nobel Prize in Physics. While neither Oppenheimer nor Snyder ever received Nobel Prizes of their own, it is evident that Penrose’s theories rested firmly on the shoulders of Oppenheimer and Snyder’s dusty giants.
Astrobite edited by Huei Sears
Featured image credit: Dey & Joshi (2019)