Title: Implications for the Hubble tension from the ages of the oldest astrophysical objects
Authors: Sunny Vagnozzi et al.
First Author’s Institution:
Kavli Institute for Cosmology (KICC) and Institute of Astronomy, University of Cambridge
Status: Preprint available on ArXiv
One of the most important concepts that has shaped our current understanding of astronomy is the expansion of the universe. Einstein showed through his theory of General Relativity that space is “stretchy,” and that the basic state of the universe on large scales is one of expansion, contraction, or perfect balance. Then, with the help of previous work done by Henrietta Leavitt, Edwin Hubble measured the distances of 46 relatively local galaxies and combined these observations with velocity (redshift) measurements from the literature, like in Figure 1 below. Not only did this work demonstrate the existence of galaxies outside the Milky Way for the first time, it showed that these galaxies were racing away from us, and ultimately, that the universe itself was expanding.
It turns out that the rate of the expansion of the universe, also known as the Hubble constant (H0), has enormous consequences for the physics underlying the cosmos, so refining the value of H0 has been a primary effort in observational astronomy. Today, there are two primary competing methods for measuring H0: one that uses local objects, in a similar effort to Hubble’s, and another that uses distant measurements and information encoded in the Cosmic Microwave Background. Over the past several years their disagreement has grown stronger and stronger, leading to what has now been dubbed the “Hubble Tension.” Why do these two measurements disagree? Is there new underlying physics yet to be discovered? Or are there systematic issues that have yet to be fully understood by either method?Let’s take a step back and get our bearings. In tackling big questions, it is always useful to first overcome smaller logical-consistency checks. Might there be a simple way we can at least set an upper limit on the Hubble constant? Are either of the two main measurements of H0 particularly problematic? Answering these questions is the goal of the paper covered by today’s astrobite.
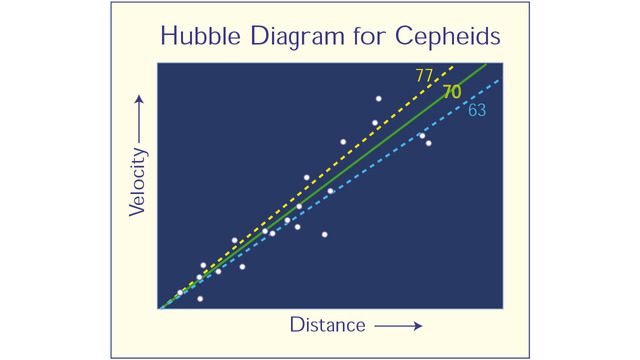
Figure 1: This is an example of a “Hubble Diagram,” which plots the distances to different galaxies and their corresponding recession velocities. Galaxies at larger distances are moving more quickly away from us as the entire universe expands. The different colored lines indicate different values of the Hubble constant in units of km/s/Mpc. Credit: NASA, ESA, STScI.
What can old objects in the Universe tell us about the Hubble constant?
One interesting feature of our current understanding of the cosmos is that at every point in time, the rate of expansion of the universe is inversely proportional to the age of the universe at that time (let’s not get into the mathematics about why that is the case, unless you really want to!). Additionally, it is assumed that every object we find in the universe must be younger than the universe itself since no object formed exactly at the moment of the Big Bang. This means that each object we find places a lower limit on the age of the universe (the universe must be at least as old as the object). By combining these two pieces of information, the authors reason that it is possible to set an upper limit on the value of H0 via the lower limit on the age of the universe. For the strongest constraints, what is then needed is a sample of old objects spanning several billion years of cosmic history.
To obtain a sample of the oldest objects in the universe spanning a wide range of cosmic time, the authors consult a suite of surveys (SDSS, CANDELS, PanSTARRS, among others) which have targeted both galaxies and quasars. After applying a series of quality cuts, the authors group these objects into redshift slices and select only the oldest in each redshift slice. The result is a catalog of object ages and their associated redshifts (Figure 2 below), which can be used to infer an upper limit on H0 using the inverse-proportionality of the age of the universe and the expansion rate.
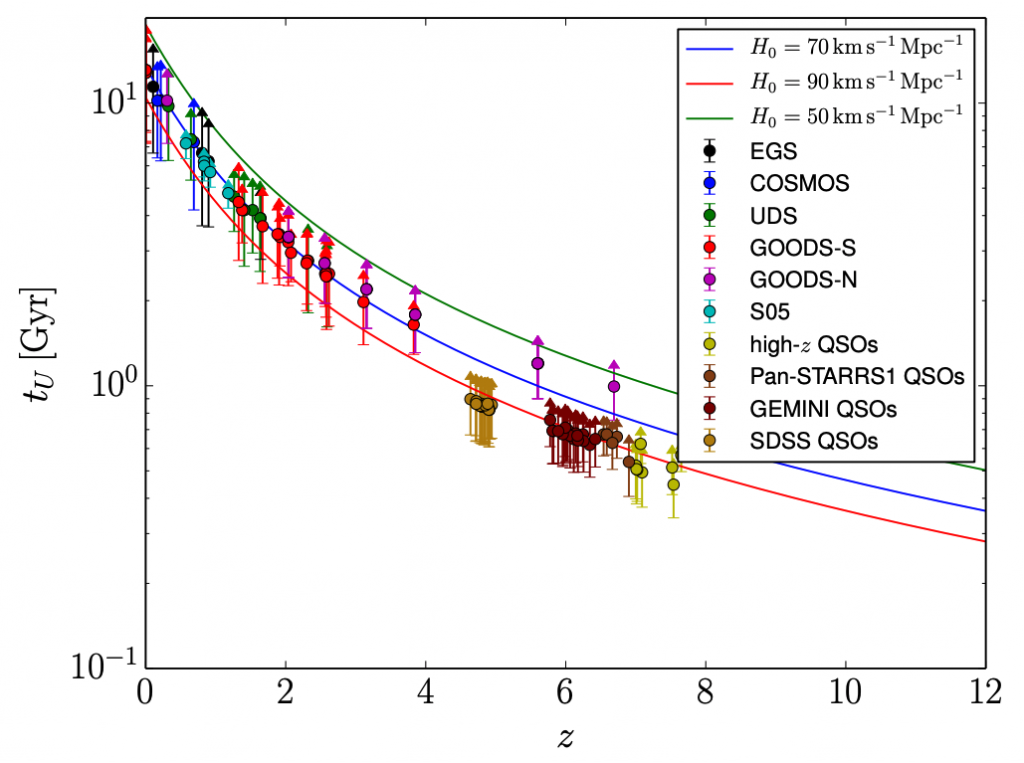
Figure 2: Ages on the y-axis and redshifts on the x-axis are shown for the objects used in this study. Each data point is colored by the survey or work from the literature that it came from. The different curves indicate the predicted age-redshift relation for different values for the Hubble constant. Fig. 1 in original work.
How to set an upper limit on H0 with old objects
With the sample of the oldest galaxies and quasars found in their sample (along with their ages and redshifts), the authors are in place to derive an upper limit on H0. To do so, the authors construct a very simple 3-parameter model which includes the Hubble constant, the matter density in the universe (Ωm, a necessary cosmological parameter for calculating the Hubble constant), and what the authors have referred to as the “incubation time” or τin (the difference between the age of the universe at a given moment and the age of the oldest objects at the point in time). The authors randomly draw different values of these parameters, and combine the matter density and Hubble constant to predict an age of the universe at a given redshift. The difference between the age of the universe, the age of the oldest objects in the universe, and the incubation time, should be zero for a perfect match. By sampling thousands of different combinations of values, the authors can map out which values are most likely (this process is generically called Markov Chain Monte Carlo). Their results are given below in a “corner plot,” which is a compact representation of both the 1-dimensional and 2-dimensional likelihood distributions of the various parameters.
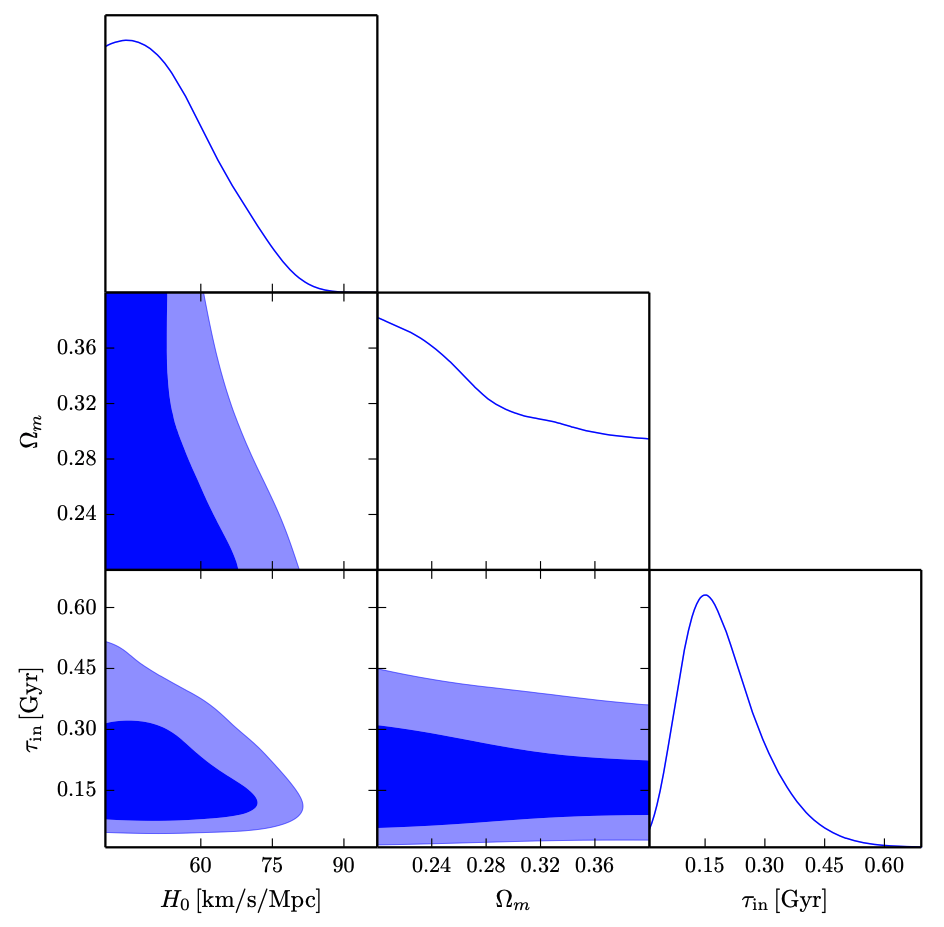
Figure 3: “Corner plot” for the likelihood distributions of the 3 parameters (Hubble constant, matter density, and incubation time) in their model. The blue lines indicate the 1-dimensional likelihood distributions of each individual parameter, while the contours indicate the joint 2-d likelihood distributions. From this result the authors derive a 95% confidence limit on the value of the Hubble constant of < 73.2 km/s/Mpc. Fig 2 in original work.
At the 95% confidence level, the authors find that H0 is constrained to be < 73.2 km/s/Mpc. Whereas the tension between Cosmic Microwave Background measurements and local measurements lead to a tension of > 4σ, the authors’ result here is only a 2σ tension with local measurements and is perfectly consistent with the CMB measurement. In general, a 2σ discrepancy (2 standard deviations of disagreement) is usually not a concern, and for most physicists, would not even be considered “evidence” of new physics. Both of the measurements (more or less) pass this test!
The authors stress here that their analysis rests strongly on the validity of the ages in their sample of old astrophysical objects and on the validity of the concordance cosmological model (also known as Λ-cold dark matter, or ΛCDM). If either of these break down, their results are no longer valid. Given the fortitude of ΛCDM (it is called the concordance model for a reason, after all!), the crucial factor here is then the ages of astrophysical objects. Constraining the ages of both galaxies and quasars is no easy task. This work can be strengthened significantly by improving our methods for estimating ages of distant objects and by finding old objects at ever increasing redshifts. Undoubtedly both of these objectives are within reach: astronomers will continue to construct samples of well-studied objects throughout the universe, and point ever more sophisticated and sensitive telescopes into the night sky. As the authors conclude, measuring the ages of objects in the universe offers a noteworthy avenue for understanding the basic laws of the cosmos.
Edited by: Haley Wahl