Title: The Exomoon Corridor for Multiple Moon Systems
Authors: Alex Teachey
First Author’s Institution: Academia Sinica Institute of Astronomy and Astrophysics, Taipei, Taiwan
Status: Accepted for publication in Monthly Notices of the Royal Astronomical Society
On Earth, we only have one moon. However, most solar system planets have many more. From Mars’ 2 to Saturn’s 82 (known) moons, all planets exterior to Earth have multiple moons. But, what about planets orbiting other stars? If they are anything like those in our outer solar system, there may be “exomoons” in systems all over the Galaxy and Universe! In the search for exoplanets, several exomoon candidates have been detected, but none are fully confirmed. Today’s paper takes a look at the “exomoon corridor” as a tool for finding these exomoons in single and multiple moon systems.
Detecting Exomoons
To find exomoons, the researchers examine time-series photometry, which telescopes like Kepler and TESS use to find transiting exoplanets. Exomoons can be detected in 3 different signals in the star’s brightness as it changes over time, or its light curve:
- Direct transit detection: A star’s apparent brightness decreases as the moon passes in front and blocks a portion of its light.
- Transit timing variations (TTVs): A moon’s gravitational pull on a planet perturbs its orbit, causing transits to happen slightly earlier or later than expected.
- Transit duration variations (TDVs): A moon’s gravitational pull on a planet perturbs its orbit, causing transits to last slightly longer or shorter than expected.
Independently, one of these three signals is not necessarily enough to prove the presence of an exomoon. The detection of two or three of them can be convincing, but these signals can be very difficult to find, as they are quite small effects and can also be caused by other planets in the system.
Detecting exomoons via TTV has recently become more feasible due to the “exomoon corridor,” described by Kipping (2021), which demonstrates that roughly 50% of exomoons should induce TTVs with very short periods that planet-planet interactions rarely do. TTVs are observed at the cadence of the planet’s orbital period around its star, so we only get one data point per transit. A moon’s orbital period around its planet will always be shorter than this. This means that TTVs caused by exomoons are always undersampled and appear in the data as longer-period orbital aliases, often between 2–4 times that of the planet around its star.
Because of this, TTVs detected in this 2–4 cycle range can quickly be identified as exomoon candidates. The mathematics behind this method, however, are based on the assumption that the planet in question only hosts one moon. Today’s paper explores whether the corridor still applies to multi-moon systems.
Multi-moon systems
Today’s author uses Rebound to model various systems with N>1 moons to see whether their TTV periods also typically fall into this corridor. 150,000 different systems were evaluated, with different planet masses, moon mass ratios, numbers of moons (between 1–5), and orbital periods. These systems are split into 3 sets:
- Fixed host: Jupiter-mass planets orbiting Sun-like stars.
- Variable host: Host star masses drawn randomly from Kepler planet systems and candidates, with randomly generated planet-star mass ratios.
- Resonant chain: Variable host planet-star system, with each moon system in a resonant-orbit chain.
Gravitational interactions can get complicated for multi-moon systems, and many of these generated may not be stable in the long-term. The more moons involved, the greater the chance for destabilizing interactions, where an object may be ejected from the system or sent into the planet’s Roche limit to be torn apart. The author eliminated highly unstable systems from the set, as these would be very short-lived and generally not found in real observations. Stability fractions for the simulated systems are shown in Figure 1. The results show that systems with low total moon to planet mass ratios were more stable than systems with higher moon mass ratios. Higher mass ratios correspond to larger, more detectable TTVs, and since these are more stable in low N systems, exomoon searches may be biased toward finding more low N systems.
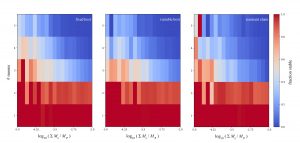
Figure 1: Heat maps of system stability with respect to moon-planet mass ratio and number of moons. We see that systems with fewer moons and lower mass ratios tend to be more stable in all three categories of simulated systems. (Figure 5 in the paper)
The author then calculates observable TTV periods for each of the remaining systems, with the distribution shown in Figure 2. We see a pile-up of short-period signals for all 3 simulations sets and all numbers of moons from 1 to 5, indicating that the exomoon corridor does indeed apply to multi-moon systems.
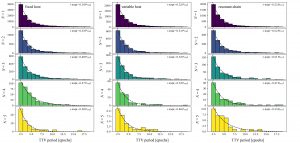
Figure 2: TTV histograms for each set of simulations and number of moons. All are highly dominated by short period, exomoon corridor-range periods. (Figure 9 in the paper)
What does this mean for the search for exomoons?
To determine whether real data show evidence for moons with this approach, the author examines different sets of transit timing observations from Kepler. They found a pile-up of short period TTVs in systems with only one known planet, systems with multiple planets, and systems with TTVs that could plausibly be explained by moons (as determined by previous work). This pile-up was not found in a sample of TTV periods for systems with confirmed planet-planet interactions, nor in the set of TTVs which could not be plausibly explained by exomoons. The results are consistent with the presence of moons in Kepler TTV data, but the author cautions against interpreting this as definitive evidence of such moons.
Ultimately, while some challenges remain in the use of the exomoon corridor method, it seems to apply to planets with 2–5 moons as it does with single moons. The majority of planets in our solar system have multiple moons (often >5), so the ability to characterize these multi-moon systems may be essential to grasping the full picture of exoplanets and their moons.
Astrobite edited by Suchitra Narayanan
Featured image credit: NASA/ESA/L. Hustak (STScI)