This guest post was written by Mark Popinchalk, a PhD candidate at the CUNY Graduate Center and Hunter College, based at the American Museum of Natural History. He studies the relationship between rotation rate and age in low mass stars. He is part of the BDNYC research group and is also a co-host for Astronomy on Tap NYC. Outside of astronomy he enjoys ultimate frisbee, bakes bread, and plays board games. His favorite color is sky-blue-pink.

——————————————————————
Authors: Brett M. Morris
Title: A Relationship Between Stellar Age and Spot Coverage
First Author’s Institution: Center for Space and Habitability, University of Bern (Bern, Switzerland)
Status: Closed access on ApJ, pre-print available on the arXiv
Let’s say we have been handed a slice of pizza (yum!), but before we get to eat it, we’re asked to calculate what fraction of the whole pizza is covered in toppings. We could measure the fraction of toppings on our one slice, but if the pizza maker applied their toppings at random and we only have one slice to go off of, it doesn’t tell us that much. The slice could be from a wide variety of potential pizzas with different topping distributions. To distinguish between these possible answers, we could try the same measurement for multiple slices (now we don’t have to share!) and hope that the topping placements even out over time.
The author of today’s paper used a similar strategy, not concerning the toppings on the surface of a pizza but instead the starspots on the surface of a star. If a star has starspots on its surface, the starspots will rotate in and out of view, changing the brightness in a periodic way that shows up in a light curve, (the measure of a star’s brightness over time). However, that change in brightness, called the “smoothed amplitude”, also has multiple solutions. The amplitude of a single light curve can be reproduced by different combinations of starspot parameters (such as size and location on the star) as well as the angle at which the star is rotating compared to us, known as the inclination.
Astronomers can make guesses about the starspots, but the inclination of the star is not easy to measure and should be random for each star. Without confirming what the inclination is, how will we know the starspot coverage? In our pizza problem we used multiple slices to try to average out the randomness of topping placement, the author of today’s paper used groups of similar stars in associations of known age to get around the randomness of each star’s inclination angle.
The author measured the smoothed amplitude of the light curves for 531 F, G, & K stars in 6 associations ranging in age from 10 Million to 4 Billion years old. From a first pass, he found that the distribution of smoothed amplitudes of the groups decreased with age, in a similar way to how stars spin down. But the author took it a step further, using an algorithm to generate synthetic light curves with various parameters including the fraction of starspot coverage, fs. With the algorithm, the author made many synthetic light curves with random inclinations, compared the synthetic smoothed amplitudes to those of the real star associations, and tuned the spot parameters of the various synthetic ones until they matched the real associations as closely as possible. The author couldn’t match all the associations perfectly, but found a similar relationship to the amplitude of the real light curves: that the fs distribution decreased with age (Figure 1).
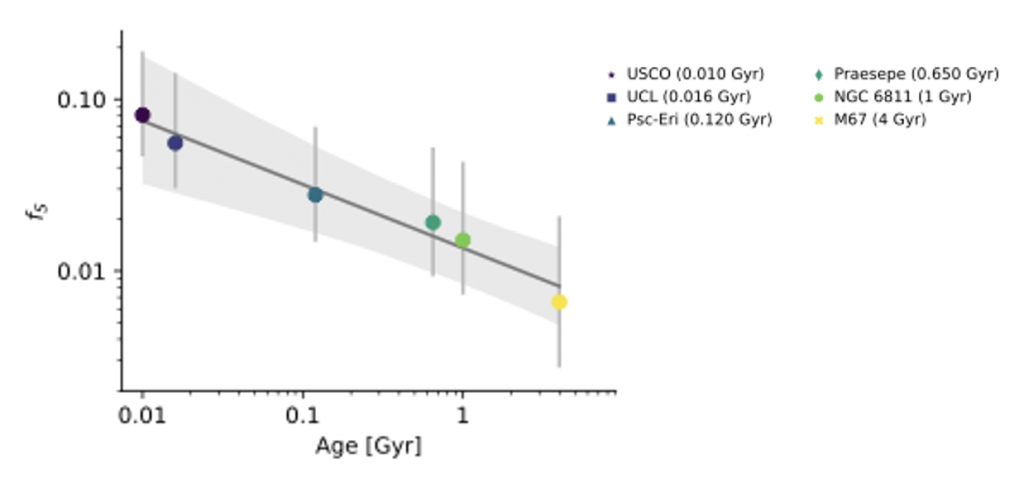
Eager to test this relationship, the author grabbed a handful of stars of known age that also host transiting exoplanets. Why transiting exoplanets? In our own solar system, the planets are within ~5 degrees of the equator of the Sun. We assume that other systems are set up the same way (exceptions are noteworthy), so if we have the correct alignment to observe a transiting planet, the star it transits is likely to be inclined with its equator towards us. Knowing the inclination removes a huge amount of possible solutions! So, using the algorithm again to create a bunch of light curves that matched that of the stars, now with the inclination set, the author saw which spot parameters worked the most often and got a distribution of fs for each star. You can see an example, including one possible surface map solution in Figure 2.
Most of the stars line up pretty well with the relation between fs and age created earlier, with the older ones falling off. The author notes that it might be worth rethinking this relationship as more complicated than a line, but to do so would require more stars older than 4 Billion years (Figure 3). Still, this result is exciting! We went from an unsolvable problem in terms of the light curve amplitude of single stars, to creating a relationship that could prove to be a useful tool for constraining ages of stars with transiting exoplanets. And that’s worth a slice of pizza.
Edited By: Huei Sears
Featured Image Adapted from NASA/SDO
