Title: Bayesian ages for early-type stars from isochrones including rotation, and a possible old age for the Hyades
Authors: Timothy D. Brandt & Chelsea X. Huang
First Author’s Institution: Institute for Advanced Study
Status: Submitted to ApJ
The Hyades cluster forms the head of Taurus the bull in the zodiac constellation. It is one of the most famous open clusters—a group of stars that all formed at the same time from the same cloud of gas. This cluster was thought to be 625 million years old, however new research suggests that the Hyades is much older. This makes for a slightly awkward situation; the Hyades underpins our understanding of stellar ages. If its age is wrong then a lot of other ages are wrong too…
To understand why the Hyades plays such an important role in stellar dating it’s necessary to explain a little bit about how the game works (and what a mess it is!).
Isochrones, models and interpolation
It can be difficult to tell the age of a main-sequence star just by looking at it; changes that happen deep in the stellar core don’t have much impact on their outward appearance. Stars do change a little in brightness over their main sequence lifetimes, and by measuring their luminosities in different colours we can use some (slightly convoluted) trickery to infer their ages. We can measure the apparent magnitude of a star in different colours—this is a pretty easy measurement, so available for lots of stars. You can almost think of it as a really low resolution spectrum. If you know how far away your star is, from parallax measurements, for example, you can figure out the star’s absolute magnitude in those colours.
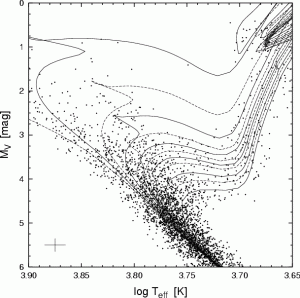
Figure 1. An example Hertzprung Russell diagram (similar to a colour-magnitude diagram, with temperature instead of colour) from this paper. Each line is an isochrone—a line of constant age for a given mass and metallicity. The age of a star is found by matching its position on the diagram to the nearest isochrone.
The next step involves matching the observations up with theoretical predictions. Complex physical models of stars are used to produce predictions of the luminosity you would expect, given a mass, metallicity and age. You can’t do this for all values of mass, metallicity and age —that would take forever! The model predictions are therefore computed on a grid; at discrete intervals of the three properties, to produce isochrones. Isochrones are lines of constant age on a colour-magnitude diagram, or Hertzprung-Russell diagram (see figure 1). Two stars that lie on the same isochrone should be the same age and their mass and metallicity define where on the isochrone they sit. By finding the position on an isochrone that is closest to your star’s position on the colour-magnitude diagram you can estimate its mass, age and metallicity. Even better—don’t simply match your star to the nearest isochrone, but interpolate across the grid to find the values of mass, metallicity and age at the exact position of your star.
I should mention by the way, this method of finding an age for a star isn’t great. It’s still the best thing we can do, but ages measured by isochrone fitting tend to have uncertainties of at least 50% and often more than 100%. That’s just because, like I said, stars don’t change their outward appearance very much over their main-sequence lifetimes.
The method outlined above is standard practise. So what’s new in this paper? Well, usually, these theoretical models that predict a luminosity for a given mass, metallicity and age don’t include the effects of stellar rotation. All stars rotate though, and some rotate quickly enough to make a big difference to their positions on the colour-magnitude diagram. Stars that rotate rapidly fling out the material around their equators, increasing their radii slightly. The equatorial parts of the star are further away from the hot stellar interior and are therefore a little cooler and less luminous. Both of these factors affect the star’s luminosity. Try to fit a rapidly rotating star to an isochrone that doesn’t take rotation into account and you may well measure the wrong age for that star.
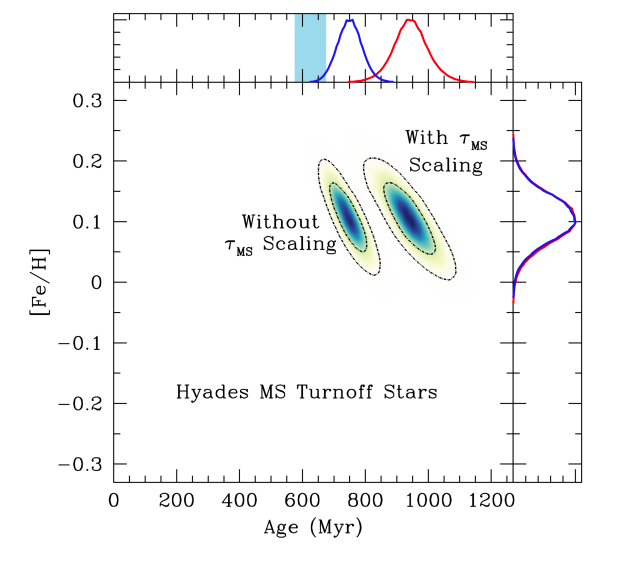
Figure 2. The marginalised posterior probability distribution of the Hyades’ age and metallicity. The two contoured regions encircle the most probable values for the age and metallicity of the cluster. The left-hand high-probability region shows the result for models without rotation. The most probable age for the Hyades, using non-rotating models is around 750 Myrs. The right-hand region shows the result for models with rotation. The most probable age for the Hyades using rotating models is around 950 million years.
The Hyades’ age problem
The authors of this paper use rotating stellar models to measure the age of the Hyades cluster and, guess what? It turns out to be older than previously thought. It’s gone from a youthful 625 million years to a, slightly less youthful but still pretty youthful 950 million years. Of course, this difference is miniscule when you consider that most Hyades stars will live for billions of years; aren’t I splitting hairs? Here’s the thing though: stellar ages are really really hard to measure for main sequence field stars, but much easier for cluster stars. That’s because they are stellar populations – they’re all the same age and roughly the same metallicity. You can fit an isochrone to an ensemble of stars —that gives you a much tighter constraint on its age (assuming the stellar models are correct, of course). For this reason, clusters are used to calibrate other stellar dating methods. Gyrochronology, for example: the method of dating a star from its mass and rotation period relies enormously on the fact that the age of the Hyades has very small error bars! If the age of the Hyades is wrong, that could have a serious domino effect. Hundreds of stars could have the incorrect age as a result.
Posteriors, posteriors, posteriors!
Everything done by the authors of this paper do is probabilistic. They don’t report one age for the Hyades, they report a probability distribution over ages (and provide samples from the posterior probability distribution). They even provide an awesome web interface where you can enter the name of a star, along with a rough estimate of metallicity (actually a metallicity prior), and it spits out the posterior probability distribution for the age of that star. The posterior probability distribution for the Hyades’ age and metallicity is shown in Figure 2.
A resolution?
This conflict may be resolved soon—the Kepler spacecraft (now reincarnated as K2) is currently observing the Hyades. It will be able to detect asteroseismic oscillations in some of its stars, revealing their true ages. Hundreds of inferences rely on the age of this cluster—unveiling the mystery will be an exciting moment for stellar astronomy!


Whoa this could be a huge domino effect! How do asteroseismic oscillations date a star? Why don’t we use this method more often to determine the ages of stars?
Asteroseismology is great for dating stars! By measuring the frequencies at which a star oscillates, you’re actually measuring the density of the star. As a star gets older it gets more dense towards the centre, so measuring the density profile of a star gives you its age. Believe me, we’re using this method wherever we can! Unfortunately, we are currently pretty much limited to just studying the brightest stars observed by the Kepler spacecraft—you need *really* precise measurement of a star’s variations in brightness over time to detect the oscillations. This is why we need both asteroseismology and clusters to calibrate other dating methods.
We do. At least there lots of efforts made to do so. The Kepler spacecraft was doing it, but the exoplanet part of the mission just got way more media coverage. It seems that exoplanets are “sexier” than stellar entrails… 😉 Oh, and Plato 2.0 will also have a part of its mission dedicated to asteroseismology. Since monitoring bright stars helps to achieve higher quality in your asteroseismic analysis, the Plato results will probably be orders of magnitudes better than the ones from Kepler. From ground you cannot do asteroseismology, which is why so far it was not used on a huge sample of stars.
If the age discrepancy in Hyades is about 300 million years, not a terribly big discrepancy, as you said, how much will that affect the age estimates for other stars? Will their ages be off by similar orders of magnitude or will the effect be greatly amplified?
Its hard to quantify exactly how much other stars’ ages will be out by. The Hyades is one of the principle clusters used for calibrating dating methods, so a lot of stellar ages could be systematically wrong as a result. To be honest though, all estimates of ages for field stars usually have whopping great uncertainties (20 – 100%), so they are probably still consistent within the error bars.
Isn’t the main effect of (modest) rotation to bring extra fuel into the core by rotational mixing? This increases the age of stars at the main sequence turn off.
Also. The new age for the Hyades in this paper is 750+/- 100 Myr. ?
There was an error in the original paper your reviewed!