Authors: Nicolas P. Cimerman, Roman R. Rafikov
First Author’s Institution: Department of Applied Mathematics and Theoretical Physics, University of Cambridge
Paper Status: Submitted to MNRAS [open access on arXiv]
Planets form in disks of gas and dust (mostly gas), which we call protoplanetary disks. During its formation, a planet affects the gas within the disk. This is what we know from numerical simulations, which show spiral arms around a planet when it is getting formed.
When astrophysicists do hydrodynamical simulations of a planet getting formed in a disk, they don’t usually expect to see an actual planet, rather they expect to see an output from the planet – something caused by an interaction between a protoplanet and a protoplanetary disk. The most general thing that you would expect to see are the spiral arms – planet-induced spiral-shaped density waves created around a protoplanet. Figure 1, panel (a) gives a visualization of such spiral arms in a protoplanetary disk. There are primary and secondary arms. By studying both of them we can understand the disk evolution. The authors of today’s paper have taken a closer look at these planet-driven spiral arms and their development over time.
When Athena ordered burgers…
The authors compared different descriptions of planet-driven density waves for two different planet masses: 0.01 and 0.25 times the parameter named thermal mass, which depends on the disk and planet parameters. This parameter makes the mass description general, which is good, because you can employ the results for different planets. These different descriptions include linear calculations (the calculations relying on solving the linearized fluid equations, which allowed the authors to demonstrate the transition into weak nonlinear behavior), solutions for the inviscid Burgers’ equations and the nonlinear simulations with the code called Athena++.
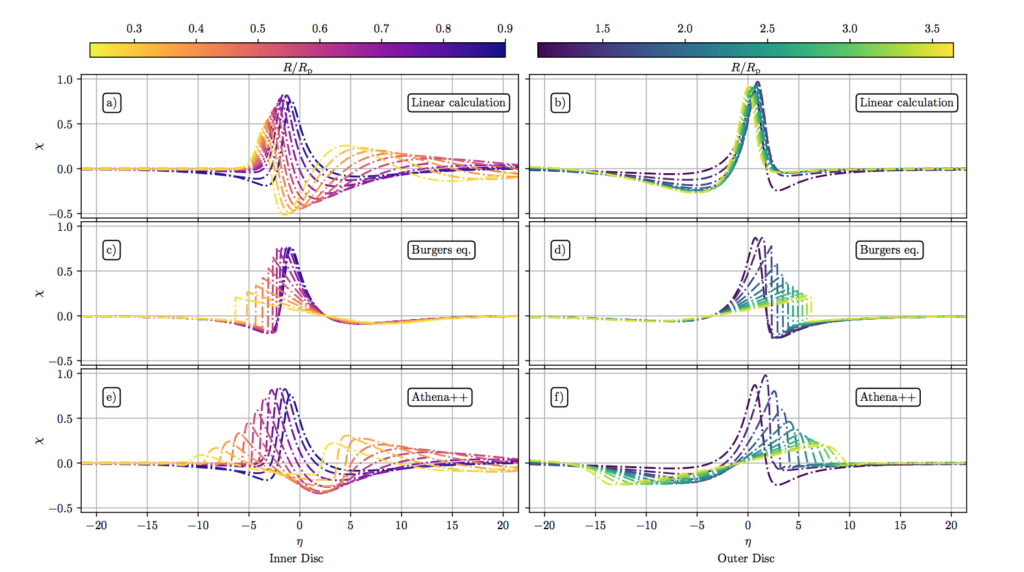
In Figure 2, you can see the representation of all three methods. For linear calculations (see panel (a) in Figure 2), a little spike for brighter colors (closer to yellow) is visible – this is an indication of secondary spiral arms appearing for radii less or equal to half the planetary orbital radius. However, in panel (c), this spike is not visible, which means that the solutions to Burgers’ equation do not capture the secondary spiral arms, but the inner and outer disks evolve similarly (panels (c) and (d)). Comparing the bottom and top rows, we can easily see the similarities between them. The authors conclude that, therefore, their implementation in Athena++ is in agreement with the linear predictions for low-mass planets. More importantly, the bottom panels, which correspond to the implementation in Athena++, capture both effects that we see in the top and middle panels. This means that the Athena++ solution combines both the linear (linear calculations) and nonlinear (Burgers’ equation) effects. This also implies that the Burgers’ equation is not representing some wave propagation physics accurately that takes place in the simulations.
Shocking results!
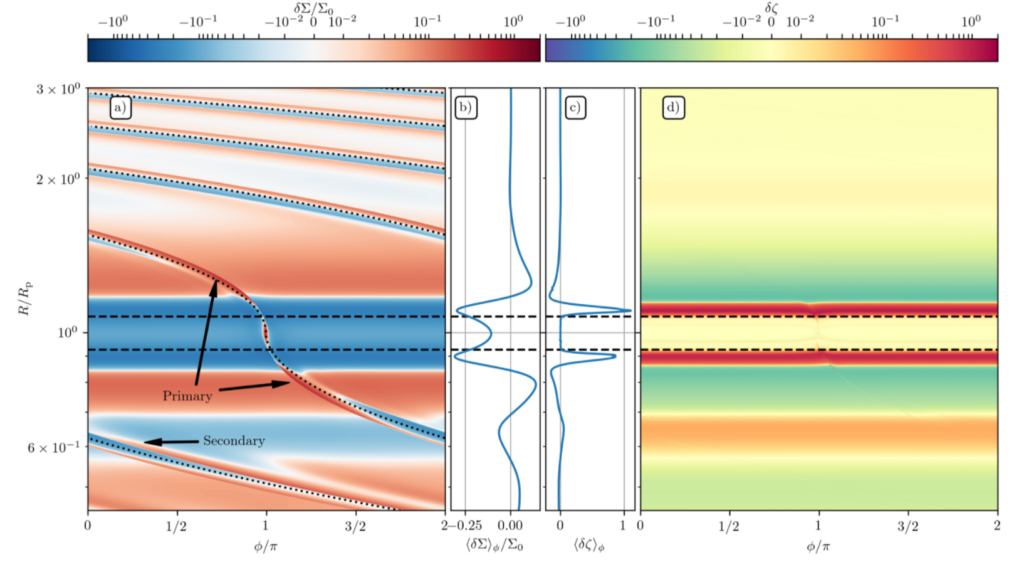
The appearance of a secondary arm is a linear effect, that is why it doesn’t appear in the solutions to Burgers’ equations. Both primary and secondary spiral arms evolve into shocks. The spikes seen in Figure 2 correspond to shocks from primary and secondary spiral arms. The second spike is not visible in panels (c) and (d) (Burgers’ equations), because the solutions to Burgers’ equations correspond to nonlinear effects and therefore don’t show the secondary spiral arms. While studying the evolution of the shock strength, the shock strength inferred from the authors’ simulations displays a second peak, which is associated with the emergence of a secondary spiral arm and its evolution into a shock.
Vortensity generation
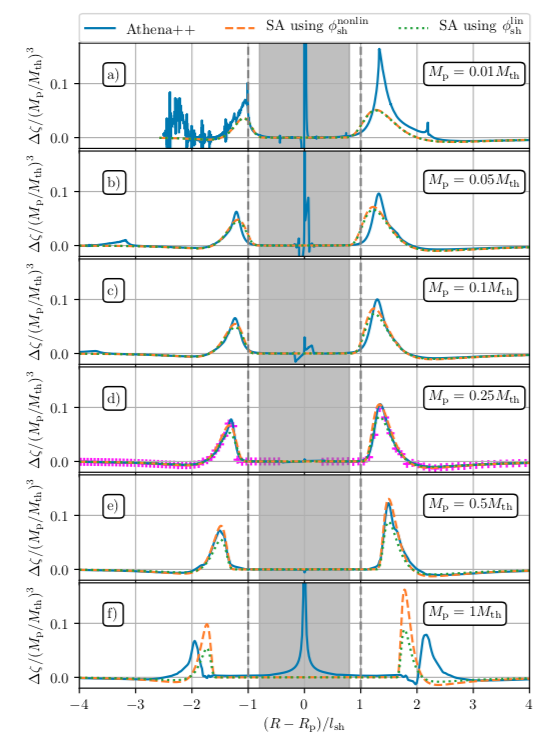
When a planet forms, it also generates swirls in the disks. To describe these swirls, we use a quantity named “vortensity,” which shows how ‘swirly’ the flow is within some local density. Here, the vortensity is generated due to the shocks in spiral waves. Note the spikes in Figure 1’s panel (c) – they show that the change in vortensity is not conserved around the shocks. The second spike, once again, represents the shock in the secondary spiral wave. One of the main results of this paper is the authors’ semi-analytical expression for the vortensity jump across the shock, which takes into account nonlinear effects. When scientists do numerical simulations, they can see some physics happening without even knowing the mathematical expressions for these phenomena. Getting mathematical expressions is another level of difficulty. In Figure 3, the authors compare their results from the semi-analytical expression and from their simulations. The blue line represents the result from the simulations, the dashed green and orange lines represent the result from the semi-analytical calculations. As you can see in Figure 3, the semi-analytical results match perfectly for planetary masses of 0.1, 0.25 and 0.5 times the thermal mass, which are just 10, 25 and 50 Earth masses, respectively (panels (c), (d) and (e)). They don’t match for lower mass planets (panels (a) and (b)) because linear effects become more important for these planets. Both results also shouldn’t match for higher mass planets because the key assumption breaks down when a planet reaches masses higher than 50 Earth masses. The authors are going to study the vortensity generation more in their next work! So, we should all stay tuned!
It is hard, folks
The main goal of this study was to verify the results of the study from 2002, and you might be thinking: why did no one thoroughly check it for almost 20 years? The answer is just: it is hard. The study required huge resolution for simulations running for a very long time. This paper will help us to better understand the appearance and evolution of planet-driven spiral arms, which itself will be a huge contribution to disk-planet interaction research. Moreover, there are observations of such arms and other kinematic signatures from the planets available now. If we understand these planet-induced effects better, we will be able to detect exoplanets in the early stages of their formation (we already have one such detected exoplanet)!
Astrobite edited by: Jana Steuer
Featured image credit: NASA/ESA/ESO/M. Benisty et al./R. Dong/Z. Zhu